Discriminate-and-Rectify Encoders: Learning from Image Transformation Sets

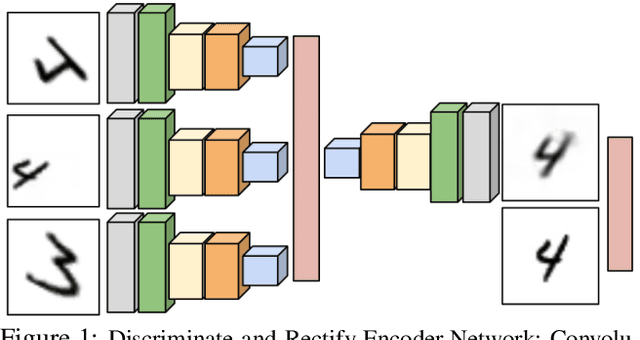
The complexity of a learning task is increased by transformations in the input space that preserve class identity. Visual object recognition for example is affected by changes in viewpoint, scale, illumination or planar transformations. While drastically altering the visual appearance, these changes are orthogonal to recognition and should not be reflected in the representation or feature encoding used for learning. We introduce a framework for weakly supervised learning of image embeddings that are robust to transformations and selective to the class distribution, using sets of transforming examples (orbit sets), deep parametrizations and a novel orbit-based loss. The proposed loss combines a discriminative, contrastive part for orbits with a reconstruction error that learns to rectify orbit transformations. The learned embeddings are evaluated in distance metric-based tasks, such as one-shot classification under geometric transformations, as well as face verification and retrieval under more realistic visual variability. Our results suggest that orbit sets, suitably computed or observed, can be used for efficient, weakly-supervised learning of semantically relevant image embeddings.

Learning with Group Invariant Features: A Kernel Perspective

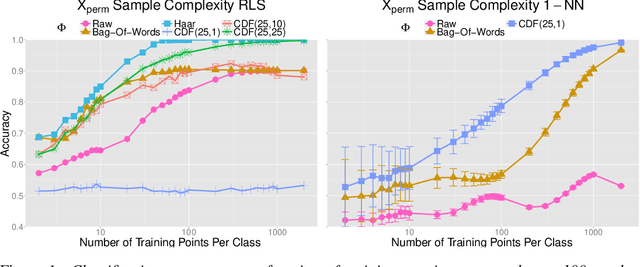
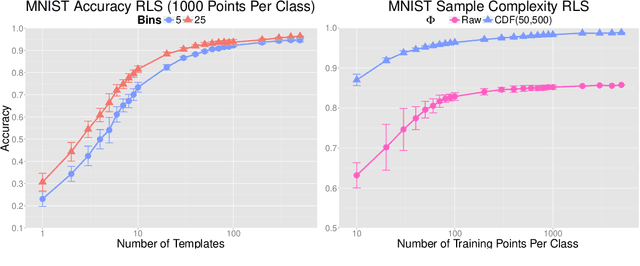
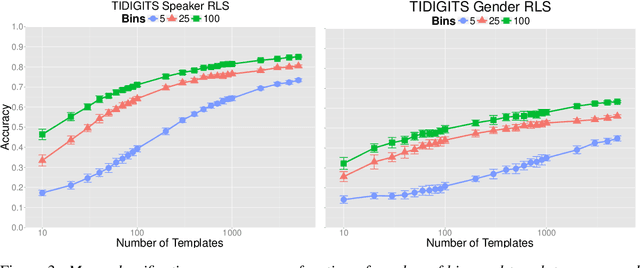
We analyze in this paper a random feature map based on a theory of invariance I-theory introduced recently. More specifically, a group invariant signal signature is obtained through cumulative distributions of group transformed random projections. Our analysis bridges invariant feature learning with kernel methods, as we show that this feature map defines an expected Haar integration kernel that is invariant to the specified group action. We show how this non-linear random feature map approximates this group invariant kernel uniformly on a set of $N$ points. Moreover, we show that it defines a function space that is dense in the equivalent Invariant Reproducing Kernel Hilbert Space. Finally, we quantify error rates of the convergence of the empirical risk minimization, as well as the reduction in the sample complexity of a learning algorithm using such an invariant representation for signal classification, in a classical supervised learning setting.

Learning An Invariant Speech Representation

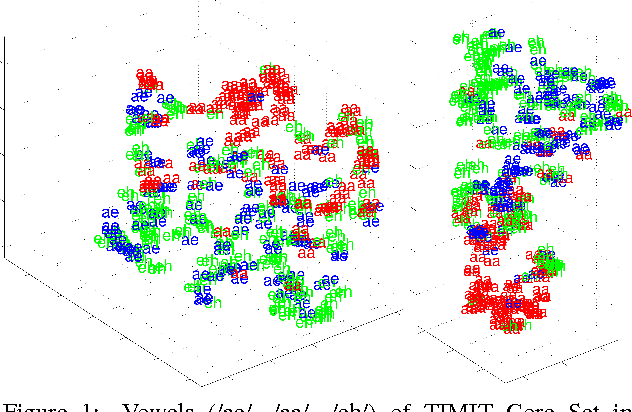
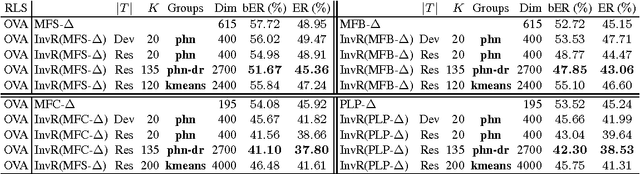
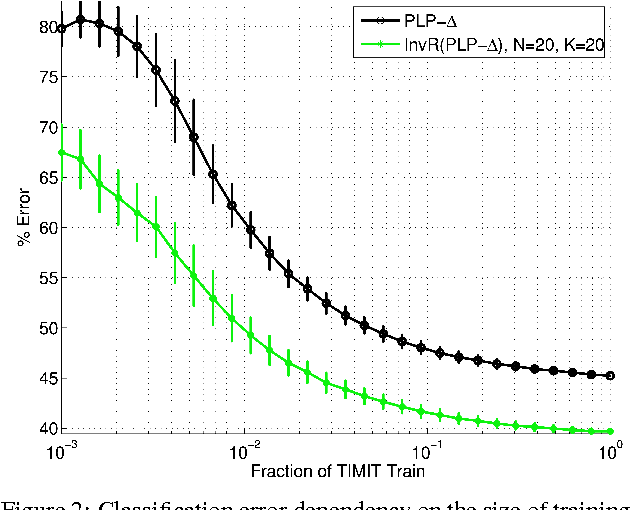
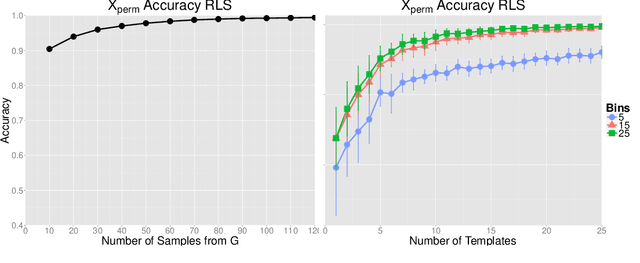
Recognition of speech, and in particular the ability to generalize and learn from small sets of labelled examples like humans do, depends on an appropriate representation of the acoustic input. We formulate the problem of finding robust speech features for supervised learning with small sample complexity as a problem of learning representations of the signal that are maximally invariant to intraclass transformations and deformations. We propose an extension of a theory for unsupervised learning of invariant visual representations to the auditory domain and empirically evaluate its validity for voiced speech sound classification. Our version of the theory requires the memory-based, unsupervised storage of acoustic templates -- such as specific phones or words -- together with all the transformations of each that normally occur. A quasi-invariant representation for a speech segment can be obtained by projecting it to each template orbit, i.e., the set of transformed signals, and computing the associated one-dimensional empirical probability distributions. The computations can be performed by modules of filtering and pooling, and extended to hierarchical architectures. In this paper, we apply a single-layer, multicomponent representation for phonemes and demonstrate improved accuracy and decreased sample complexity for vowel classification compared to standard spectral, cepstral and perceptual features.

A Deep Representation for Invariance And Music Classification

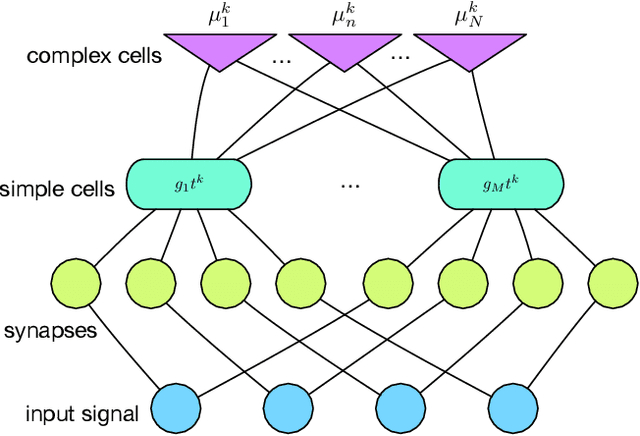
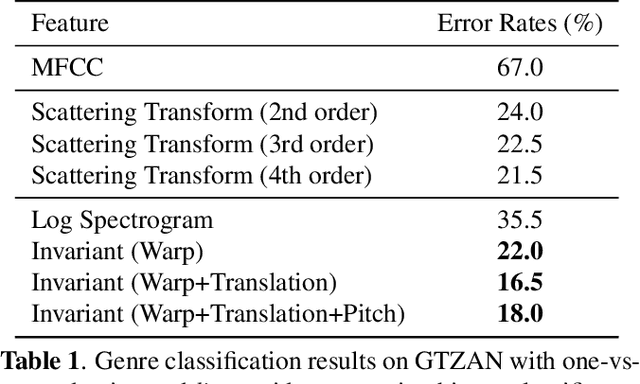
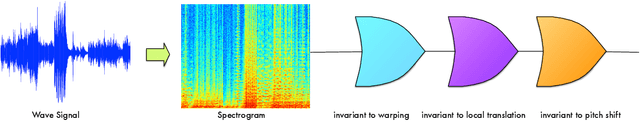
Representations in the auditory cortex might be based on mechanisms similar to the visual ventral stream; modules for building invariance to transformations and multiple layers for compositionality and selectivity. In this paper we propose the use of such computational modules for extracting invariant and discriminative audio representations. Building on a theory of invariance in hierarchical architectures, we propose a novel, mid-level representation for acoustical signals, using the empirical distributions of projections on a set of templates and their transformations. Under the assumption that, by construction, this dictionary of templates is composed from similar classes, and samples the orbit of variance-inducing signal transformations (such as shift and scale), the resulting signature is theoretically guaranteed to be unique, invariant to transformations and stable to deformations. Modules of projection and pooling can then constitute layers of deep networks, for learning composite representations. We present the main theoretical and computational aspects of a framework for unsupervised learning of invariant audio representations, empirically evaluated on music genre classification.

Online Learning, Stability, and Stochastic Gradient Descent

In batch learning, stability together with existence and uniqueness of the solution corresponds to well-posedness of Empirical Risk Minimization (ERM) methods; recently, it was proved that CV_loo stability is necessary and sufficient for generalization and consistency of ERM. In this note, we introduce CV_on stability, which plays a similar note in online learning. We show that stochastic gradient descent (SDG) with the usual hypotheses is CVon stable and we then discuss the implications of CV_on stability for convergence of SGD.