Inception: Efficiently Computable Misinformation Attacks on Markov Games

We study security threats to Markov games due to information asymmetry and misinformation. We consider an attacker player who can spread misinformation about its reward function to influence the robust victim player's behavior. Given a fixed fake reward function, we derive the victim's policy under worst-case rationality and present polynomial-time algorithms to compute the attacker's optimal worst-case policy based on linear programming and backward induction. Then, we provide an efficient inception ("planting an idea in someone's mind") attack algorithm to find the optimal fake reward function within a restricted set of reward functions with dominant strategies. Importantly, our methods exploit the universal assumption of rationality to compute attacks efficiently. Thus, our work exposes a security vulnerability arising from standard game assumptions under misinformation.

Optimal Attack and Defense for Reinforcement Learning

To ensure the usefulness of Reinforcement Learning (RL) in real systems, it is crucial to ensure they are robust to noise and adversarial attacks. In adversarial RL, an external attacker has the power to manipulate the victim agent's interaction with the environment. We study the full class of online manipulation attacks, which include (i) state attacks, (ii) observation attacks (which are a generalization of perceived-state attacks), (iii) action attacks, and (iv) reward attacks. We show the attacker's problem of designing a stealthy attack that maximizes its own expected reward, which often corresponds to minimizing the victim's value, is captured by a Markov Decision Process (MDP) that we call a meta-MDP since it is not the true environment but a higher level environment induced by the attacked interaction. We show that the attacker can derive optimal attacks by planning in polynomial time or learning with polynomial sample complexity using standard RL techniques. We argue that the optimal defense policy for the victim can be computed as the solution to a stochastic Stackelberg game, which can be further simplified into a partially-observable turn-based stochastic game (POTBSG). Neither the attacker nor the victim would benefit from deviating from their respective optimal policies, thus such solutions are truly robust. Although the defense problem is NP-hard, we show that optimal Markovian defenses can be computed (learned) in polynomial time (sample complexity) in many scenarios.

Minimally Modifying a Markov Game to Achieve Any Nash Equilibrium and Value

We study the game modification problem, where a benevolent game designer or a malevolent adversary modifies the reward function of a zero-sum Markov game so that a target deterministic or stochastic policy profile becomes the unique Markov perfect Nash equilibrium and has a value within a target range, in a way that minimizes the modification cost. We characterize the set of policy profiles that can be installed as the unique equilibrium of some game, and establish sufficient and necessary conditions for successful installation. We propose an efficient algorithm, which solves a convex optimization problem with linear constraints and then performs random perturbation, to obtain a modification plan with a near-optimal cost.

VISER: A Tractable Solution Concept for Games with Information Asymmetry

Many real-world games suffer from information asymmetry: one player is only aware of their own payoffs while the other player has the full game information. Examples include the critical domain of security games and adversarial multi-agent reinforcement learning. Information asymmetry renders traditional solution concepts such as Strong Stackelberg Equilibrium (SSE) and Robust-Optimization Equilibrium (ROE) inoperative. We propose a novel solution concept called VISER (Victim Is Secure, Exploiter best-Responds). VISER enables an external observer to predict the outcome of such games. In particular, for security applications, VISER allows the victim to better defend itself while characterizing the most damaging attacks available to the attacker. We show that each player's VISER strategy can be computed independently in polynomial time using linear programming (LP). We also extend VISER to its Markov-perfect counterpart for Markov games, which can be solved efficiently using a series of LPs.

On Faking a Nash Equilibrium

We characterize offline data poisoning attacks on Multi-Agent Reinforcement Learning (MARL), where an attacker may change a data set in an attempt to install a (potentially fictitious) unique Markov-perfect Nash equilibrium. We propose the unique Nash set, namely the set of games, specified by their Q functions, with a specific joint policy being the unique Nash equilibrium. The unique Nash set is central to poisoning attacks because the attack is successful if and only if data poisoning pushes all plausible games inside it. The unique Nash set generalizes the reward polytope commonly used in inverse reinforcement learning to MARL. For zero-sum Markov games, both the inverse Nash set and the set of plausible games induced by data are polytopes in the Q function space. We exhibit a linear program to efficiently compute the optimal poisoning attack. Our work sheds light on the structure of data poisoning attacks on offline MARL, a necessary step before one can design more robust MARL algorithms.

Reward Poisoning Attacks on Offline Multi-Agent Reinforcement Learning

We expose the danger of reward poisoning in offline multi-agent reinforcement learning (MARL), whereby an attacker can modify the reward vectors to different learners in an offline data set while incurring a poisoning cost. Based on the poisoned data set, all rational learners using some confidence-bound-based MARL algorithm will infer that a target policy - chosen by the attacker and not necessarily a solution concept originally - is the Markov perfect dominant strategy equilibrium for the underlying Markov Game, hence they will adopt this potentially damaging target policy in the future. We characterize the exact conditions under which the attacker can install a target policy. We further show how the attacker can formulate a linear program to minimize its poisoning cost. Our work shows the need for robust MARL against adversarial attacks.

Game Redesign in No-regret Game Playing

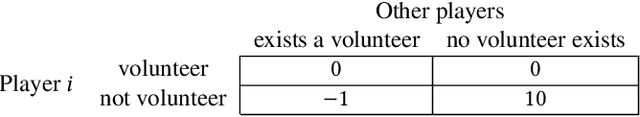
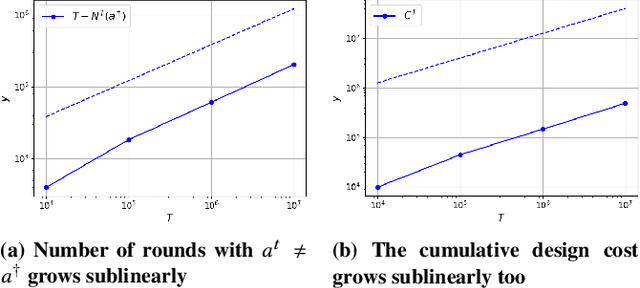
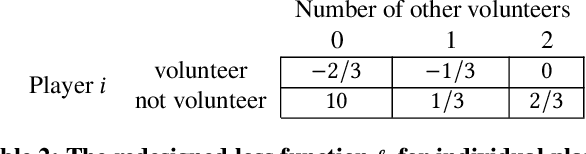
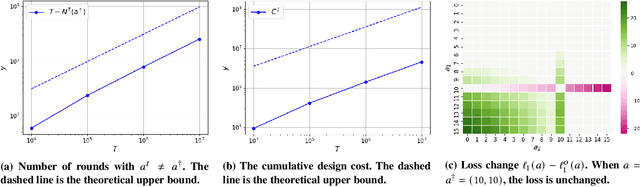
We study the game redesign problem in which an external designer has the ability to change the payoff function in each round, but incurs a design cost for deviating from the original game. The players apply no-regret learning algorithms to repeatedly play the changed games with limited feedback. The goals of the designer are to (i) incentivize all players to take a specific target action profile frequently; and (ii) incur small cumulative design cost. We present game redesign algorithms with the guarantee that the target action profile is played in T-o(T) rounds while incurring only o(T) cumulative design cost. Game redesign describes both positive and negative applications: a benevolent designer who incentivizes players to take a target action profile with better social welfare compared to the solution of the original game, or a malicious attacker whose target action profile benefits themselves but not the players. Simulations on four classic games confirm the effectiveness of our proposed redesign algorithms.