Bernstein-von Mises for Adaptively Collected Data

Uncertainty quantification (UQ) for adaptively collected data, such as that coming from adaptive experiments, bandits, or reinforcement learning, is necessary for critical elements of data collection such as ensuring safety and conducting after-study inference. The data's adaptivity creates significant challenges for frequentist UQ, yet Bayesian UQ remains the same as if the data were independent and identically distributed (i.i.d.), making it an appealing and commonly used approach. Bayesian UQ requires the (correct) specification of a prior distribution while frequentist UQ does not, but for i.i.d. data the celebrated Bernstein-von Mises theorem shows that as the sample size grows, the prior 'washes out' and Bayesian UQ becomes frequentist-valid, implying that the choice of prior need not be a major impediment to Bayesian UQ as it makes no difference asymptotically. This paper for the first time extends the Bernstein-von Mises theorem to adaptively collected data, proving asymptotic equivalence between Bayesian UQ and Wald-type frequentist UQ in this challenging setting. Our result showing this asymptotic agreement does not require the standard stability condition required by works studying validity of Wald-type frequentist UQ; in cases where stability is satisfied, our results combined with these prior studies of frequentist UQ imply frequentist validity of Bayesian UQ. Counterintuitively however, they also provide a negative result that Bayesian UQ is not asymptotically frequentist valid when stability fails, despite the fact that the prior washes out and Bayesian UQ asymptotically matches standard Wald-type frequentist UQ. We empirically validate our theory (positive and negative) via a range of simulations.

Evaluating the Effectiveness of Index-Based Treatment Allocation

When resources are scarce, an allocation policy is needed to decide who receives a resource. This problem occurs, for instance, when allocating scarce medical resources and is often solved using modern ML methods. This paper introduces methods to evaluate index-based allocation policies -- that allocate a fixed number of resources to those who need them the most -- by using data from a randomized control trial. Such policies create dependencies between agents, which render the assumptions behind standard statistical tests invalid and limit the effectiveness of estimators. Addressing these challenges, we translate and extend recent ideas from the statistics literature to present an efficient estimator and methods for computing asymptotically correct confidence intervals. This enables us to effectively draw valid statistical conclusions, a critical gap in previous work. Our extensive experiments validate our methodology in practical settings, while also showcasing its statistical power. We conclude by proposing and empirically verifying extensions of our methodology that enable us to reevaluate a past randomized control trial to evaluate different ML allocation policies in the context of a mHealth program, drawing previously invisible conclusions.

A Spectral Approach to Off-Policy Evaluation for POMDPs

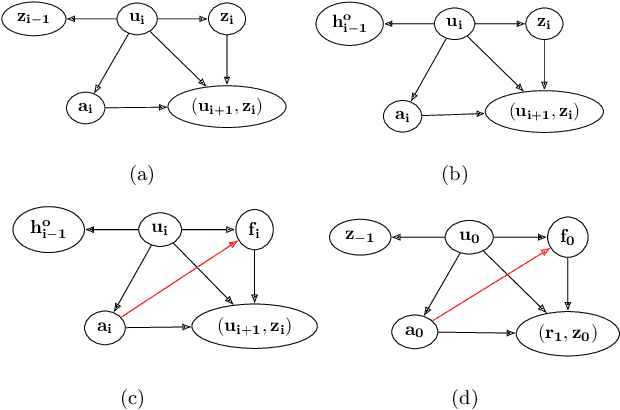
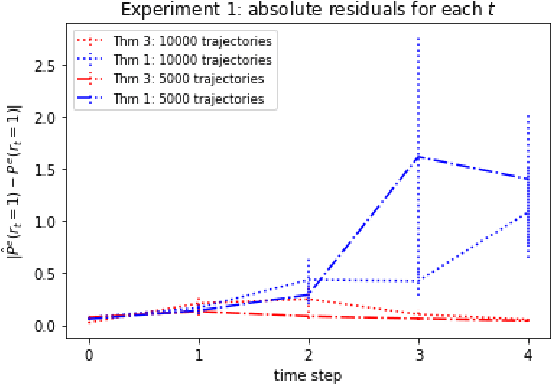
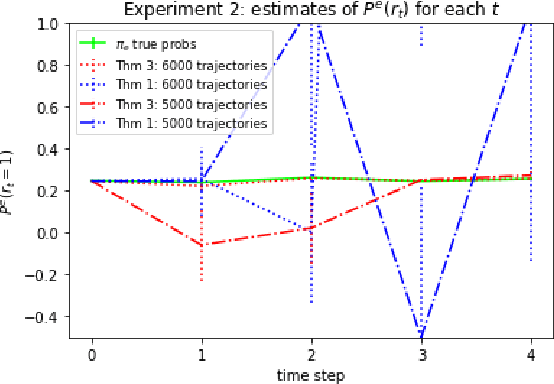
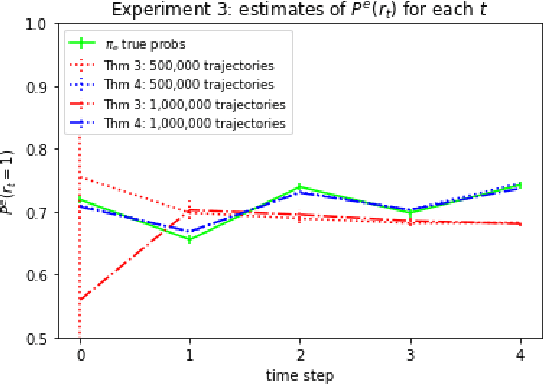
We consider off-policy evaluation (OPE) in Partially Observable Markov Decision Processes, where the evaluation policy depends only on observable variables but the behavior policy depends on latent states (Tennenholtz et al. (2020a)). Prior work on this problem uses a causal identification strategy based on one-step observable proxies of the hidden state, which relies on the invertibility of certain one-step moment matrices. In this work, we relax this requirement by using spectral methods and extending one-step proxies both into the past and future. We empirically compare our OPE methods to existing ones and demonstrate their improved prediction accuracy and greater generality. Lastly, we derive a separate Importance Sampling (IS) algorithm which relies on rank, distinctness, and positivity conditions, and not on the strict sufficiency conditions of observable trajectories with respect to the reward and hidden-state structure required by Tennenholtz et al. (2020a).

PAC Bounds for Imitation and Model-based Batch Learning of Contextual Markov Decision Processes

We consider the problem of batch multi-task reinforcement learning with observed context descriptors, motivated by its application to personalized medical treatment. In particular, we study two general classes of learning algorithms: direct policy learning (DPL), an imitation-learning based approach which learns from expert trajectories, and model-based learning. First, we derive sample complexity bounds for DPL, and then show that model-based learning from expert actions can, even with a finite model class, be impossible. After relaxing the conditions under which the model-based approach is expected to learn by allowing for greater coverage of state-action space, we provide sample complexity bounds for model-based learning with finite model classes, showing that there exist model classes with sample complexity exponential in their statistical complexity. We then derive a sample complexity upper bound for model-based learning based on a measure of concentration of the data distribution. Our results give formal justification for imitation learning over model-based learning in this setting.