Learning to Wait: Synchronizing Agents with the Physical World

Real-world agentic tasks, unlike synchronous Markov Decision Processes (MDPs), often involve non-blocking actions with variable latencies, creating a fundamental \textit{Temporal Gap} between action initiation and completion. Existing environment-side solutions, such as blocking wrappers or frequent polling, either limit scalability or dilute the agent's context window with redundant observations. In this work, we propose an \textbf{Agent-side Approach} that empowers Large Language Models (LLMs) to actively align their \textit{Cognitive Timeline} with the physical world. By extending the Code-as-Action paradigm to the temporal domain, agents utilize semantic priors and In-Context Learning (ICL) to predict precise waiting durations (\texttt{time.sleep(t)}), effectively synchronizing with asynchronous environment without exhaustive checking. Experiments in a simulated Kubernetes cluster demonstrate that agents can precisely calibrate their internal clocks to minimize both query overhead and execution latency, validating that temporal awareness is a learnable capability essential for autonomous evolution in open-ended environments.

Convergence analysis of OT-Flow for sample generation

Deep generative models aim to learn the underlying distribution of data and generate new ones. Despite the diversity of generative models and their high-quality generation performance in practice, most of them lack rigorous theoretical convergence proofs. In this work, we aim to establish some convergence results for OT-Flow, one of the deep generative models. First, by reformulating the framework of OT-Flow model, we establish the $\Gamma$-convergence of the formulation of OT-flow to the corresponding optimal transport (OT) problem as the regularization term parameter $\alpha$ goes to infinity. Second, since the loss function will be approximated by Monte Carlo method in training, we established the convergence between the discrete loss function and the continuous one when the sample number $N$ goes to infinity as well. Meanwhile, the approximation capability of the neural network provides an upper bound for the discrete loss function of the minimizers. The proofs in both aspects provide convincing assurances for OT-Flow.

A deep learning framework for geodesics under spherical Wasserstein-Fisher-Rao metric and its application for weighted sample generation

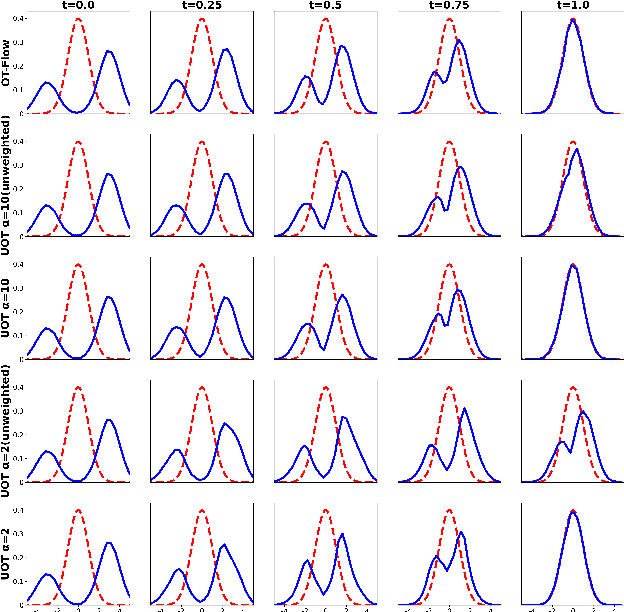
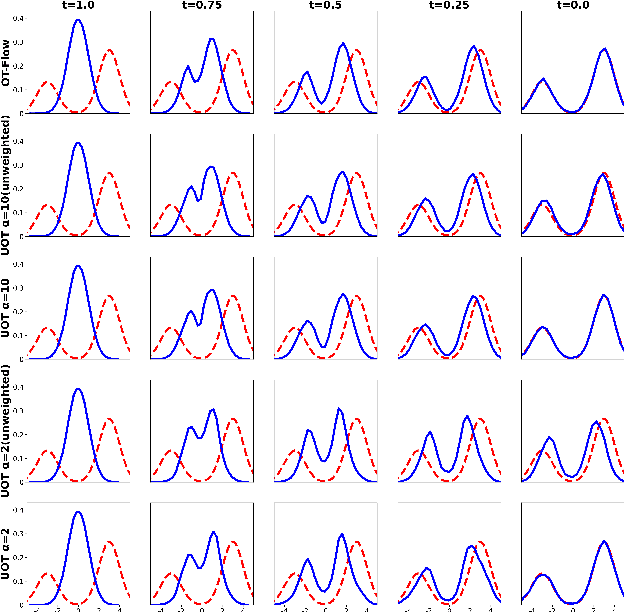
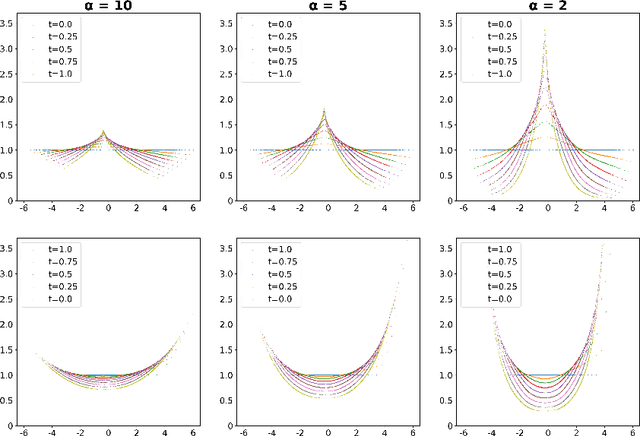
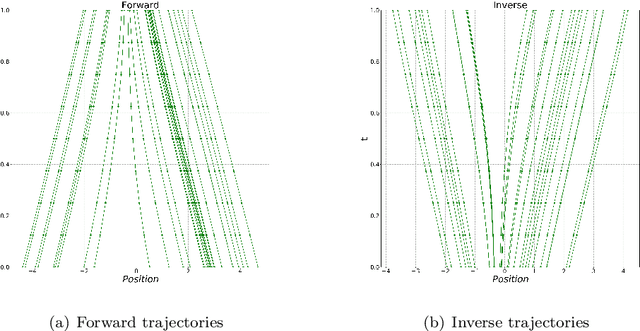
Wasserstein-Fisher-Rao (WFR) distance is a family of metrics to gauge the discrepancy of two Radon measures, which takes into account both transportation and weight change. Spherical WFR distance is a projected version of WFR distance for probability measures so that the space of Radon measures equipped with WFR can be viewed as metric cone over the space of probability measures with spherical WFR. Compared to the case for Wasserstein distance, the understanding of geodesics under the spherical WFR is less clear and still an ongoing research focus. In this paper, we develop a deep learning framework to compute the geodesics under the spherical WFR metric, and the learned geodesics can be adopted to generate weighted samples. Our approach is based on a Benamou-Brenier type dynamic formulation for spherical WFR. To overcome the difficulty in enforcing the boundary constraint brought by the weight change, a Kullback-Leibler (KL) divergence term based on the inverse map is introduced into the cost function. Moreover, a new regularization term using the particle velocity is introduced as a substitute for the Hamilton-Jacobi equation for the potential in dynamic formula. When used for sample generation, our framework can be beneficial for applications with given weighted samples, especially in the Bayesian inference, compared to sample generation with previous flow models.