Optimal and Private Learning from Human Response Data

Item response theory (IRT) is the study of how people make probabilistic decisions, with diverse applications in education testing, recommendation systems, among others. The Rasch model of binary response data, one of the most fundamental models in IRT, remains an active area of research with important practical significance. Recently, Nguyen and Zhang (2022) proposed a new spectral estimation algorithm that is efficient and accurate. In this work, we extend their results in two important ways. Firstly, we obtain a refined entrywise error bound for the spectral algorithm, complementing the `average error' $\ell_2$ bound in their work. Notably, under mild sampling conditions, the spectral algorithm achieves the minimax optimal error bound (modulo a log factor). Building on the refined analysis, we also show that the spectral algorithm enjoys optimal sample complexity for top-$K$ recovery (e.g., identifying the best $K$ items from approval/disapproval response data), explaining the empirical findings in the previous work. Our second contribution addresses an important but understudied topic in IRT: privacy. Despite the human-centric applications of IRT, there has not been any proposed privacy-preserving mechanism in the literature. We develop a private extension of the spectral algorithm, leveraging its unique Markov chain formulation and the discrete Gaussian mechanism (Canonne et al., 2020). Experiments show that our approach is significantly more accurate than the baselines in the low-to-moderate privacy regime.

Efficient and Accurate Learning of Mixtures of Plackett-Luce Models

Mixture models of Plackett-Luce (PL) -- one of the most fundamental ranking models -- are an active research area of both theoretical and practical significance. Most previously proposed parameter estimation algorithms instantiate the EM algorithm, often with random initialization. However, such an initialization scheme may not yield a good initial estimate and the algorithms require multiple restarts, incurring a large time complexity. As for the EM procedure, while the E-step can be performed efficiently, maximizing the log-likelihood in the M-step is difficult due to the combinatorial nature of the PL likelihood function (Gormley and Murphy 2008). Therefore, previous authors favor algorithms that maximize surrogate likelihood functions (Zhao et al. 2018, 2020). However, the final estimate may deviate from the true maximum likelihood estimate as a consequence. In this paper, we address these known limitations. We propose an initialization algorithm that can provide a provably accurate initial estimate and an EM algorithm that maximizes the true log-likelihood function efficiently. Experiments on both synthetic and real datasets show that our algorithm is competitive in terms of accuracy and speed to baseline algorithms, especially on datasets with a large number of items.

Leave-one-out Singular Subspace Perturbation Analysis for Spectral Clustering

The singular subspaces perturbation theory is of fundamental importance in probability and statistics. It has various applications across different fields. We consider two arbitrary matrices where one is a leave-one-column-out submatrix of the other one and establish a novel perturbation upper bound for the distance between two corresponding singular subspaces. It is well-suited for mixture models and results in a sharper and finer statistical analysis than classical perturbation bounds such as Wedin's Theorem. Powered by this leave-one-out perturbation theory, we provide a deterministic entrywise analysis for the performance of the spectral clustering under mixture models. Our analysis leads to an explicit exponential error rate for the clustering of sub-Gaussian mixture models. For the mixture of isotropic Gaussians, the rate is optimal under a weaker signal-to-noise condition than that of L\"offler et al. (2021).

Uncertainty quantification in the Bradley-Terry-Luce model

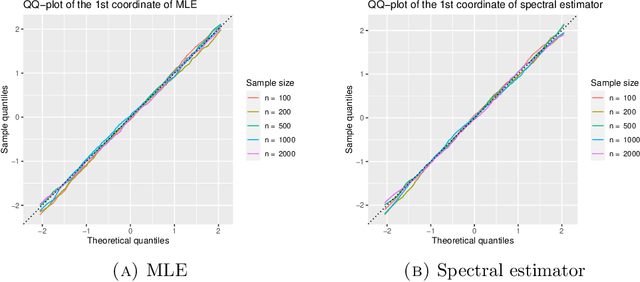
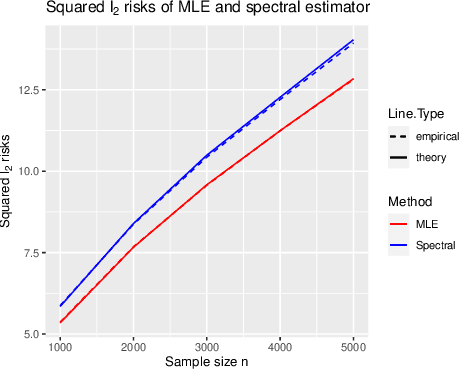
The Bradley-Terry-Luce (BTL) model is a benchmark model for pairwise comparisons between individuals. Despite recent progress on the first-order asymptotics of several popular procedures, the understanding of uncertainty quantification in the BTL model remains largely incomplete, especially when the underlying comparison graph is sparse. In this paper, we fill this gap by focusing on two estimators that have received much recent attention: the maximum likelihood estimator (MLE) and the spectral estimator. Using a unified proof strategy, we derive sharp and uniform non-asymptotic expansions for both estimators in the sparsest possible regime (up to some poly-logarithmic factors) of the underlying comparison graph. These expansions allow us to obtain: (i) finite-dimensional central limit theorems for both estimators; (ii) construction of confidence intervals for individual ranks; (iii) optimal constant of $\ell_2$ estimation, which is achieved by the MLE but not by the spectral estimator. Our proof is based on a self-consistent equation of the second-order remainder vector and a novel leave-two-out analysis.

Optimal Orthogonal Group Synchronization and Rotation Group Synchronization

We study the statistical estimation problem of orthogonal group synchronization and rotation group synchronization. The model is $Y_{ij} = Z_i^* Z_j^{*T} + \sigma W_{ij}\in\mathbb{R}^{d\times d}$ where $W_{ij}$ is a Gaussian random matrix and $Z_i^*$ is either an orthogonal matrix or a rotation matrix, and each $Y_{ij}$ is observed independently with probability $p$. We analyze an iterative polar decomposition algorithm for the estimation of $Z^*$ and show it has an error of $(1+o(1))\frac{\sigma^2 d(d-1)}{2np}$ when initialized by spectral methods. A matching minimax lower bound is further established which leads to the optimality of the proposed algorithm as it achieves the exact minimax risk.

Optimal Full Ranking from Pairwise Comparisons

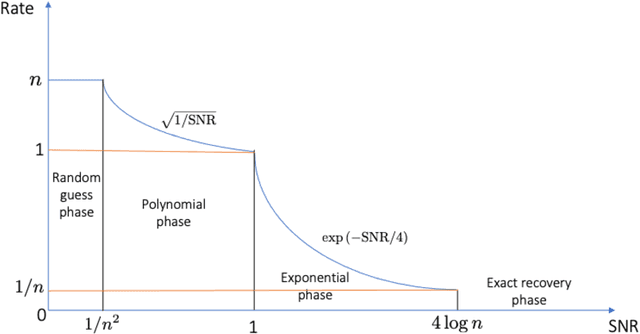
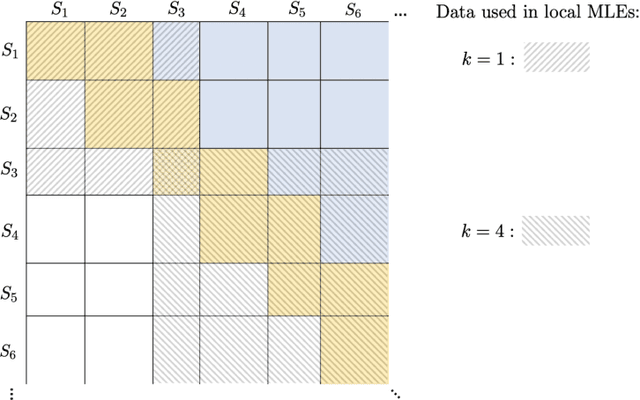
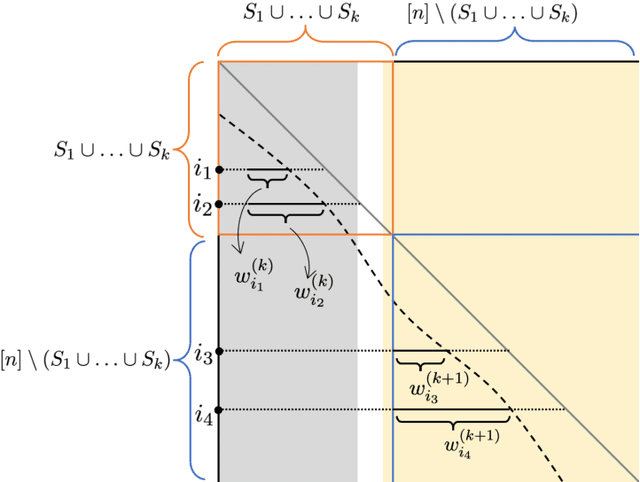
We consider the problem of ranking $n$ players from partial pairwise comparison data under the Bradley-Terry-Luce model. For the first time in the literature, the minimax rate of this ranking problem is derived with respect to the Kendall's tau distance that measures the difference between two rank vectors by counting the number of inversions. The minimax rate of ranking exhibits a transition between an exponential rate and a polynomial rate depending on the magnitude of the signal-to-noise ratio of the problem. To the best of our knowledge, this phenomenon is unique to full ranking and has not been seen in any other statistical estimation problem. To achieve the minimax rate, we propose a divide-and-conquer ranking algorithm that first divides the $n$ players into groups of similar skills and then computes local MLE within each group. The optimality of the proposed algorithm is established by a careful approximate independence argument between the two steps.

Optimal Clustering in Anisotropic Gaussian Mixture Models

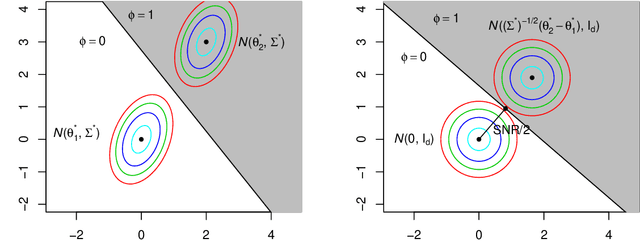
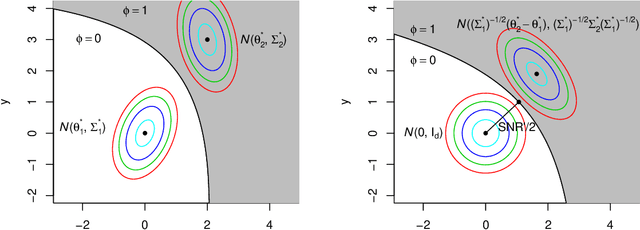
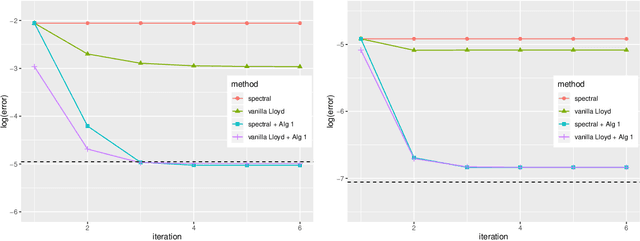
We study the clustering task under anisotropic Gaussian Mixture Models where the covariance matrices from different clusters are unknown and are not necessarily the identical matrix. We characterize the dependence of signal-to-noise ratios on the cluster centers and covariance matrices and obtain the minimax lower bound for the clustering problem. In addition, we propose a computationally feasible procedure and prove it achieves the optimal rate within a few iterations. The proposed procedure is a hard EM type algorithm, and it can also be seen as a variant of the Lloyd's algorithm that is adjusted to the anisotropic covariance matrices.

SDP Achieves Exact Minimax Optimality in Phase Synchronization

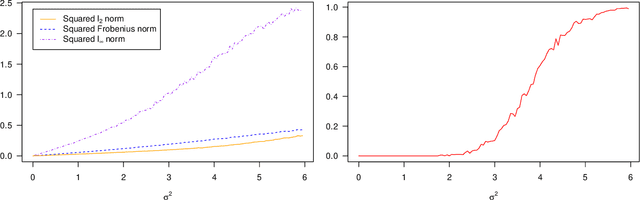
We study the phase synchronization problem with noisy measurements $Y=z^*z^{*H}+\sigma W\in\mathbb{C}^{n\times n}$, where $z^*$ is an $n$-dimensional complex unit-modulus vector and $W$ is a complex-valued Gaussian random matrix. It is assumed that each entry $Y_{jk}$ is observed with probability $p$. We prove that an SDP relaxation of the MLE achieves the error bound $(1+o(1))\frac{\sigma^2}{2np}$ under a normalized squared $\ell_2$ loss. This result matches the minimax lower bound of the problem, and even the leading constant is sharp. The analysis of the SDP is based on an equivalent non-convex programming whose solution can be characterized as a fixed point of the generalized power iteration lifted to a higher dimensional space. This viewpoint unifies the proofs of the statistical optimality of three different methods: MLE, SDP, and generalized power method. The technique is also applied to the analysis of the SDP for $\mathbb{Z}_2$ synchronization, and we achieve the minimax optimal error $\exp\left(-(1-o(1))\frac{np}{2\sigma^2}\right)$ with a sharp constant in the exponent.

Partial Recovery for Top-$k$ Ranking: Optimality of MLE and Sub-Optimality of Spectral Method

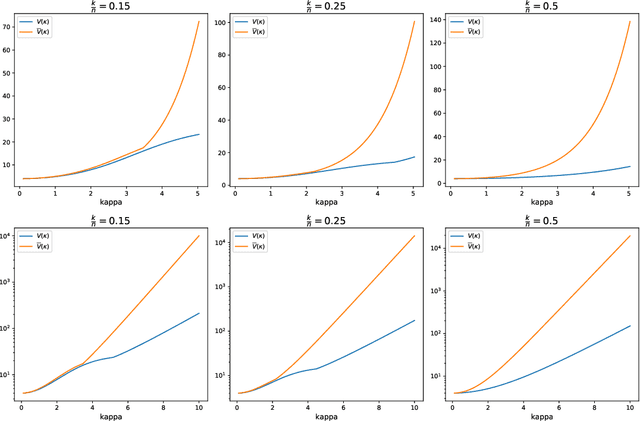
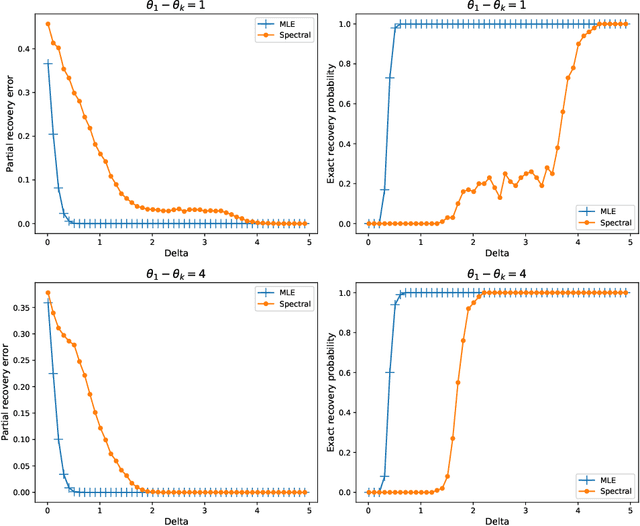
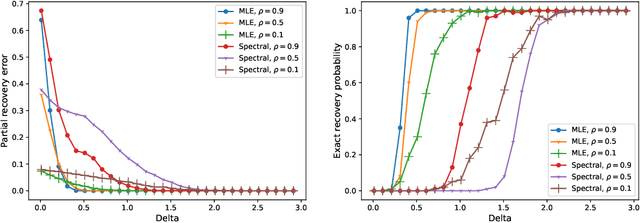
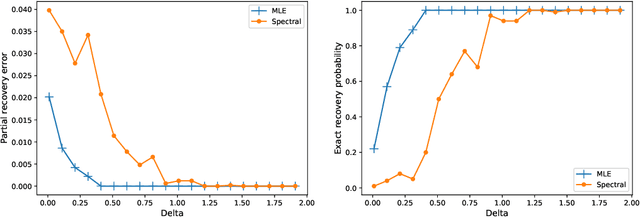
Given partially observed pairwise comparison data generated by the Bradley-Terry-Luce (BTL) model, we study the problem of top-$k$ ranking. That is, to optimally identify the set of top-$k$ players. We derive the minimax rate with respect to a normalized Hamming loss. This provides the first result in the literature that characterizes the partial recovery error in terms of the proportion of mistakes for top-$k$ ranking. We also derive the optimal signal to noise ratio condition for the exact recovery of the top-$k$ set. The maximum likelihood estimator (MLE) is shown to achieve both optimal partial recovery and optimal exact recovery. On the other hand, we show another popular algorithm, the spectral method, is in general sub-optimal. Our results complement the recent work by Chen et al. (2019) that shows both the MLE and the spectral method achieve the optimal sample complexity for exact recovery. It turns out the leading constants of the sample complexity are different for the two algorithms. Another contribution that may be of independent interest is the analysis of the MLE without any penalty or regularization for the BTL model. This closes an important gap between theory and practice in the literature of ranking.

Iterative Algorithm for Discrete Structure Recovery

We propose a general modeling and algorithmic framework for discrete structure recovery that can be applied to a wide range of problems. Under this framework, we are able to study the recovery of clustering labels, ranks of players, and signs of regression coefficients from a unified perspective. A simple iterative algorithm is proposed for discrete structure recovery, which generalizes methods including Lloyd's algorithm and the iterative feature matching algorithm. A linear convergence result for the proposed algorithm is established in this paper under appropriate abstract conditions on stochastic errors and initialization. We illustrate our general theory by applying it on three representative problems: clustering in Gaussian mixture model, approximate ranking, and sign recovery in compressed sensing, and show that minimax rate is achieved in each case.