Beyond Accuracy: A Geometric Stability Analysis of Large Language Models in Chess Evaluation

The evaluation of Large Language Models (LLMs) in complex reasoning domains typically relies on performance alignment with ground-truth oracles. In the domain of chess, this standard manifests as accuracy benchmarks against strong engines like Stockfish. However, high scalar accuracy does not necessarily imply robust conceptual understanding. This paper argues that standard accuracy metrics fail to distinguish between genuine geometric reasoning and the superficial memorization of canonical board states. To address this gap, we propose a Geometric Stability Framework, a novel evaluation methodology that rigorously tests model consistency under invariant transformations-including board rotation, mirror symmetry, color inversion, and format conversion. We applied this framework to a comparative analysis of six state-of-the-art LLMs including GPT-5.1, Claude Sonnet 4.5, and Kimi K2 Turbo, utilizing a dataset of approximately 3,000 positions. Our results reveal a significant Accuracy-Stability Paradox. While models such as GPT-5.1 achieve near-optimal accuracy on standard positions, they exhibit catastrophic degradation under geometric perturbation, specifically in rotation tasks where error rates surge by over 600%. This disparity suggests a reliance on pattern matching over abstract spatial logic. Conversely, Claude Sonnet 4.5 and Kimi K2 Turbo demonstrate superior dual robustness, maintaining high consistency across all transformation axes. Furthermore, we analyze the trade-off between helpfulness and safety, identifying Gemini 2.5 Flash as the leader in illegal state rejection (96.0%). We conclude that geometric stability provides an orthogonal and essential metric for AI evaluation, offering a necessary proxy for disentangling reasoning capabilities from data contamination and overfitting in large-scale models.

QNNRepair: Quantized Neural Network Repair

We present QNNRepair, the first method in the literature for repairing quantized neural networks (QNNs). QNNRepair aims to improve the accuracy of a neural network model after quantization. It accepts the full-precision and weight-quantized neural networks and a repair dataset of passing and failing tests. At first, QNNRepair applies a software fault localization method to identify the neurons that cause performance degradation during neural network quantization. Then, it formulates the repair problem into a linear programming problem of solving neuron weights parameters, which corrects the QNN's performance on failing tests while not compromising its performance on passing tests. We evaluate QNNRepair with widely used neural network architectures such as MobileNetV2, ResNet, and VGGNet on popular datasets, including high-resolution images. We also compare QNNRepair with the state-of-the-art data-free quantization method SQuant. According to the experiment results, we conclude that QNNRepair is effective in improving the quantized model's performance in most cases. Its repaired models have 24% higher accuracy than SQuant's in the independent validation set, especially for the ImageNet dataset.

AIREPAIR: A Repair Platform for Neural Networks

We present AIREPAIR, a platform for repairing neural networks. It features the integration of existing network repair tools. Based on AIREPAIR, one can run different repair methods on the same model, thus enabling the fair comparison of different repair techniques. We evaluate AIREPAIR with three state-of-the-art repair tools on popular deep-learning datasets and models. Our evaluation confirms the utility of AIREPAIR, by comparing and analyzing the results from different repair techniques. A demonstration is available at https://youtu.be/UkKw5neeWhw.

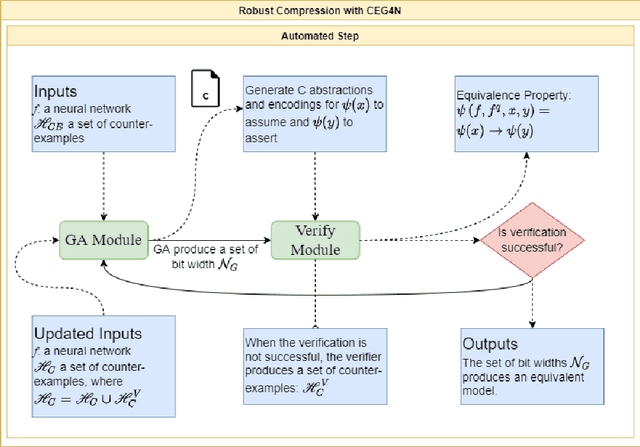
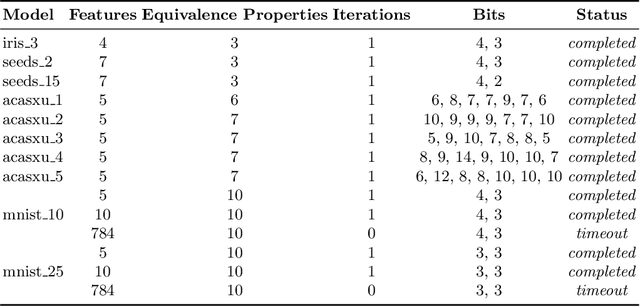
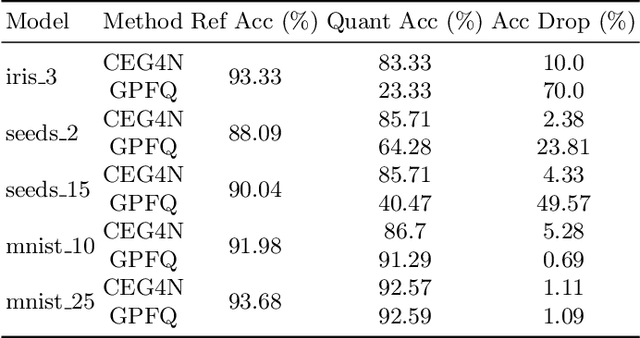
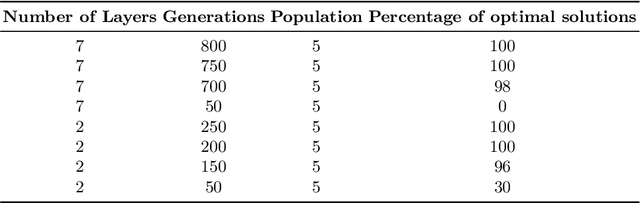
CEG4N: Counter-Example Guided Neural Network Quantization Refinement

Neural networks are essential components of learning-based software systems. However, their high compute, memory, and power requirements make using them in low resources domains challenging. For this reason, neural networks are often quantized before deployment. Existing quantization techniques tend to degrade the network accuracy. We propose Counter-Example Guided Neural Network Quantization Refinement (CEG4N). This technique combines search-based quantization and equivalence verification: the former minimizes the computational requirements, while the latter guarantees that the network's output does not change after quantization. We evaluate CEG4N~on a diverse set of benchmarks, including large and small networks. Our technique successfully quantizes the networks in our evaluation while producing models with up to 72% better accuracy than state-of-the-art techniques.

QNNVerifier: A Tool for Verifying Neural Networks using SMT-Based Model Checking

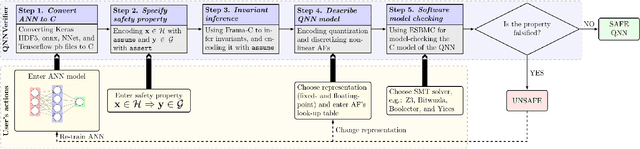
QNNVerifier is the first open-source tool for verifying implementations of neural networks that takes into account the finite word-length (i.e. quantization) of their operands. The novel support for quantization is achieved by employing state-of-the-art software model checking (SMC) techniques. It translates the implementation of neural networks to a decidable fragment of first-order logic based on satisfiability modulo theories (SMT). The effects of fixed- and floating-point operations are represented through direct implementations given a hardware-determined precision. Furthermore, QNNVerifier allows to specify bespoke safety properties and verify the resulting model with different verification strategies (incremental and k-induction) and SMT solvers. Finally, QNNVerifier is the first tool that combines invariant inference via interval analysis and discretization of non-linear activation functions to speed up the verification of neural networks by orders of magnitude. A video presentation of QNNVerifier is available at https://youtu.be/7jMgOL41zTY

Verifying Quantized Neural Networks using SMT-Based Model Checking

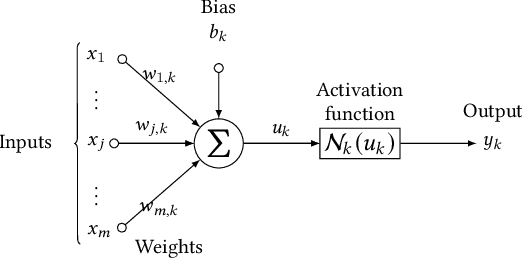
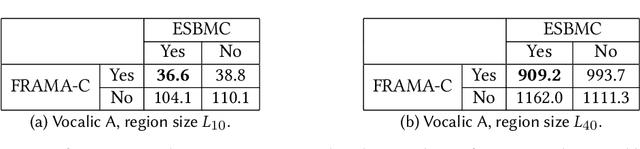
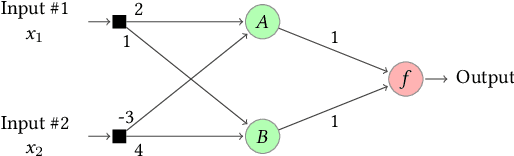
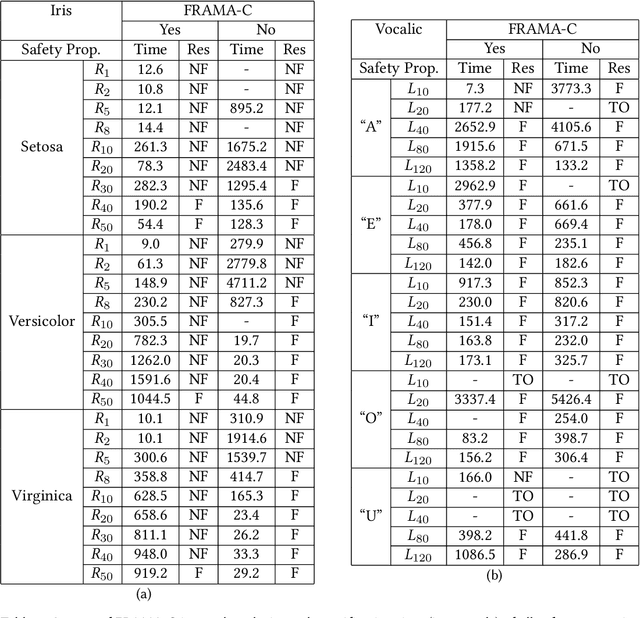
Artificial Neural Networks (ANNs) are being deployed on an increasing number of safety-critical applications, including autonomous cars and medical diagnosis. However, concerns about their reliability have been raised due to their black-box nature and apparent fragility to adversarial attacks. Here, we develop and evaluate a symbolic verification framework using incremental model checking (IMC) and satisfiability modulo theories (SMT) to check for vulnerabilities in ANNs. More specifically, we propose several ANN-related optimizations for IMC, including invariant inference via interval analysis and the discretization of non-linear activation functions. With this, we can provide guarantees on the safe behavior of ANNs implemented both in floating-point and fixed-point (quantized) arithmetic. In this regard, our verification approach was able to verify and produce adversarial examples for 52 test cases spanning image classification and general machine learning applications. For small- to medium-sized ANN, our approach completes most of its verification runs in minutes. Moreover, in contrast to most state-of-the-art methods, our approach is not restricted to specific choices of activation functions or non-quantized representations.