Graph Neural Networks for Forecasting Multivariate Realized Volatility with Spillover Effects

We present a novel methodology for modeling and forecasting multivariate realized volatilities using customized graph neural networks to incorporate spillover effects across stocks. The proposed model offers the benefits of incorporating spillover effects from multi-hop neighbors, capturing nonlinear relationships, and flexible training with different loss functions. Our empirical findings provide compelling evidence that incorporating spillover effects from multi-hop neighbors alone does not yield a clear advantage in terms of predictive accuracy. However, modeling nonlinear spillover effects enhances the forecasting accuracy of realized volatilities, particularly for short-term horizons of up to one week. Moreover, our results consistently indicate that training with the Quasi-likelihood loss leads to substantial improvements in model performance compared to the commonly-used mean squared error. A comprehensive series of empirical evaluations in alternative settings confirm the robustness of our results.

On the Impact of Sample Size in Reconstructing Graph Signals

Reconstructing a signal on a graph from observations on a subset of the vertices is a fundamental problem in the field of graph signal processing. It is often assumed that adding additional observations to an observation set will reduce the expected reconstruction error. We show that under the setting of noisy observation and least-squares reconstruction this is not always the case, characterising the behaviour both theoretically and experimentally.

Structure-Aware Robustness Certificates for Graph Classification

Certifying the robustness of a graph-based machine learning model poses a critical challenge for safety. Current robustness certificates for graph classifiers guarantee output invariance with respect to the total number of node pair flips (edge addition or edge deletion), which amounts to an $l_{0}$ ball centred on the adjacency matrix. Although theoretically attractive, this type of isotropic structural noise can be too restrictive in practical scenarios where some node pairs are more critical than others in determining the classifier's output. The certificate, in this case, gives a pessimistic depiction of the robustness of the graph model. To tackle this issue, we develop a randomised smoothing method based on adding an anisotropic noise distribution to the input graph structure. We show that our process generates structural-aware certificates for our classifiers, whereby the magnitude of robustness certificates can vary across different pre-defined structures of the graph. We demonstrate the benefits of these certificates in both synthetic and real-world experiments.

Bayesian Optimisation of Functions on Graphs

The increasing availability of graph-structured data motivates the task of optimising over functions defined on the node set of graphs. Traditional graph search algorithms can be applied in this case, but they may be sample-inefficient and do not make use of information about the function values; on the other hand, Bayesian optimisation is a class of promising black-box solvers with superior sample efficiency, but it has been scarcely been applied to such novel setups. To fill this gap, we propose a novel Bayesian optimisation framework that optimises over functions defined on generic, large-scale and potentially unknown graphs. Through the learning of suitable kernels on graphs, our framework has the advantage of adapting to the behaviour of the target function. The local modelling approach further guarantees the efficiency of our method. Extensive experiments on both synthetic and real-world graphs demonstrate the effectiveness of the proposed optimisation framework.

Graph Classification Gaussian Processes via Spectral Features

Graph classification aims to categorise graphs based on their structure and node attributes. In this work, we propose to tackle this task using tools from graph signal processing by deriving spectral features, which we then use to design two variants of Gaussian process models for graph classification. The first variant uses spectral features based on the distribution of energy of a node feature signal over the spectrum of the graph. We show that even such a simple approach, having no learned parameters, can yield competitive performance compared to strong neural network and graph kernel baselines. A second, more sophisticated variant is designed to capture multi-scale and localised patterns in the graph by learning spectral graph wavelet filters, obtaining improved performance on synthetic and real-world data sets. Finally, we show that both models produce well calibrated uncertainty estimates, enabling reliable decision making based on the model predictions.

DRew: Dynamically Rewired Message Passing with Delay

Message passing neural networks (MPNNs) have been shown to suffer from the phenomenon of over-squashing that causes poor performance for tasks relying on long-range interactions. This can be largely attributed to message passing only occurring locally, over a node's immediate neighbours. Rewiring approaches attempting to make graphs 'more connected', and supposedly better suited to long-range tasks, often lose the inductive bias provided by distance on the graph since they make distant nodes communicate instantly at every layer. In this paper we propose a framework, applicable to any MPNN architecture, that performs a layer-dependent rewiring to ensure gradual densification of the graph. We also propose a delay mechanism that permits skip connections between nodes depending on the layer and their mutual distance. We validate our approach on several long-range tasks and show that it outperforms graph Transformers and multi-hop MPNNs.

Transductive Kernels for Gaussian Processes on Graphs

Kernels on graphs have had limited options for node-level problems. To address this, we present a novel, generalized kernel for graphs with node feature data for semi-supervised learning. The kernel is derived from a regularization framework by treating the graph and feature data as two Hilbert spaces. We also show how numerous kernel-based models on graphs are instances of our design. A kernel defined this way has transductive properties, and this leads to improved ability to learn on fewer training points, as well as better handling of highly non-Euclidean data. We demonstrate these advantages using synthetic data where the distribution of the whole graph can inform the pattern of the labels. Finally, by utilizing a flexible polynomial of the graph Laplacian within the kernel, the model also performed effectively in semi-supervised classification on graphs of various levels of homophily.

Learning Hypergraphs From Signals With Dual Smoothness Prior

The construction of a meaningful hypergraph topology is the key to processing signals with high-order relationships that involve more than two entities. Learning the hypergraph structure from the observed signals to capture the intrinsic relationships among the entities becomes crucial when a hypergraph topology is not readily available in the datasets. There are two challenges that lie at the heart of this problem: 1) how to handle the huge search space of potential hyperedges, and 2) how to define meaningful criteria to measure the relationship between the signals observed on nodes and the hypergraph structure. In this paper, to address the first challenge, we adopt the assumption that the ideal hypergraph structure can be derived from a learnable graph structure that captures the pairwise relations within signals. Further, we propose a hypergraph learning framework with a novel dual smoothness prior that reveals a mapping between the observed node signals and the hypergraph structure, whereby each hyperedge corresponds to a subgraph with both node signal smoothness and edge signal smoothness in the learnable graph structure. Finally, we conduct extensive experiments to evaluate the proposed framework on both synthetic and real world datasets. Experiments show that our proposed framework can efficiently infer meaningful hypergraph topologies from observed signals.

Unrolled Graph Learning for Multi-Agent Collaboration

Multi-agent learning has gained increasing attention to tackle distributed machine learning scenarios under constrictions of data exchanging. However, existing multi-agent learning models usually consider data fusion under fixed and compulsory collaborative relations among agents, which is not as flexible and autonomous as human collaboration. To fill this gap, we propose a distributed multi-agent learning model inspired by human collaboration, in which the agents can autonomously detect suitable collaborators and refer to collaborators' model for better performance. To implement such adaptive collaboration, we use a collaboration graph to indicate the pairwise collaborative relation. The collaboration graph can be obtained by graph learning techniques based on model similarity between different agents. Since model similarity can not be formulated by a fixed graphical optimization, we design a graph learning network by unrolling, which can learn underlying similar features among potential collaborators. By testing on both regression and classification tasks, we validate that our proposed collaboration model can figure out accurate collaborative relationship and greatly improve agents' learning performance.

Learning to Infer Structures of Network Games

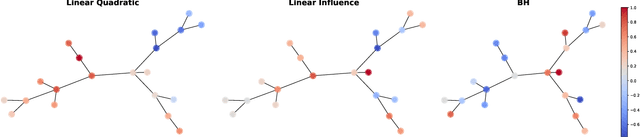
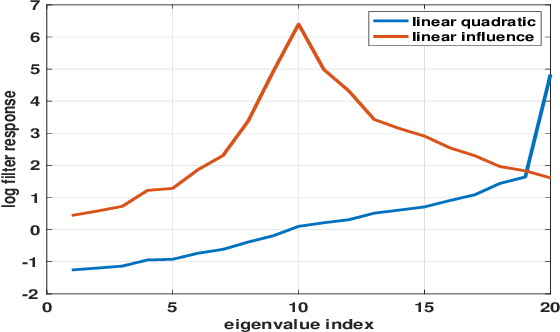
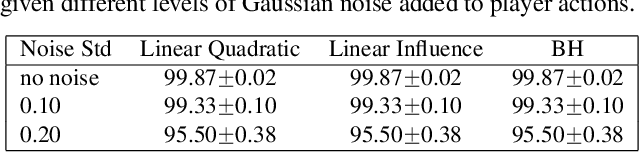
Strategic interactions between a group of individuals or organisations can be modelled as games played on networks, where a player's payoff depends not only on their actions but also on those of their neighbours. Inferring the network structure from observed game outcomes (equilibrium actions) is an important problem with numerous potential applications in economics and social sciences. Existing methods mostly require the knowledge of the utility function associated with the game, which is often unrealistic to obtain in real-world scenarios. We adopt a transformer-like architecture which correctly accounts for the symmetries of the problem and learns a mapping from the equilibrium actions to the network structure of the game without explicit knowledge of the utility function. We test our method on three different types of network games using both synthetic and real-world data, and demonstrate its effectiveness in network structure inference and superior performance over existing methods.