A Spatial Sigma-Delta Approach to Mitigation of Power Amplifier Distortions in Massive MIMO Downlink

In massive multiple-input multiple-output (MIMO) downlink systems, the physical implementation of the base stations (BSs) requires the use of cheap and power-efficient power amplifiers (PAs) to avoid high hardware cost and high power consumption. However, such PAs usually have limited linear amplification ranges. Nonlinear distortions arising from operation beyond the linear amplification ranges can significantly degrade system performance. Existing approaches to handle the nonlinear distortions, such as digital predistortion (DPD), typically require accurate knowledge, or acquisition, of the PA transfer function. In this paper, we present a new concept for mitigation of the PA distortions. Assuming a uniform linear array (ULA) at the BS, the idea is to apply a Sigma-Delta ($\Sigma \Delta$) modulator to spatially shape the PA distortions to the high-angle region. By having the system operating in the low-angle region, the received signals are less affected by the PA distortions. To demonstrate the potential of this spatial $\Sigma \Delta$ approach, we study the application of our approach to the multi-user MIMO-orthogonal frequency division modulation (OFDM) downlink scenario. A symbol-level precoding (SLP) scheme and a zero-forcing (ZF) precoding scheme, with the new design requirement by the spatial $\Sigma \Delta$ approach being taken into account, are developed. Numerical simulations are performed to show the effectiveness of the developed $\Sigma \Delta$ precoding schemes.

An Efficient Global Algorithm for One-Bit Maximum-Likelihood MIMO Detection

There has been growing interest in implementing massive MIMO systems by one-bit analog-to-digital converters (ADCs), which have the benefit of reducing the power consumption and hardware complexity. One-bit MIMO detection arises in such a scenario. It aims to detect the multiuser signals from the one-bit quantized received signals in an uplink channel. In this paper, we consider one-bit maximum-likelihood (ML) MIMO detection in massive MIMO systems, which amounts to solving a large-scale nonlinear integer programming problem. We propose an efficient global algorithm for solving the one-bit ML MIMO detection problem. We first reformulate the problem as a mixed integer linear programming (MILP) problem that has a massive number of linear constraints. The massive number of linear constraints raises computational challenges. To solve the MILP problem efficiently, we custom build a light-weight branch-and-bound tree search algorithm, where the linear constraints are incrementally added during the tree search procedure and only small-size linear programming subproblems need to be solved at each iteration. We provide simulation results to demonstrate the efficiency of the proposed method.

Accelerated and Deep Expectation Maximization for One-Bit MIMO-OFDM Detection

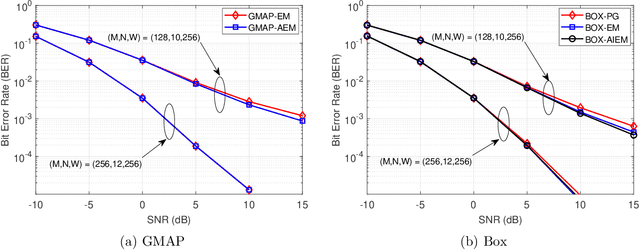
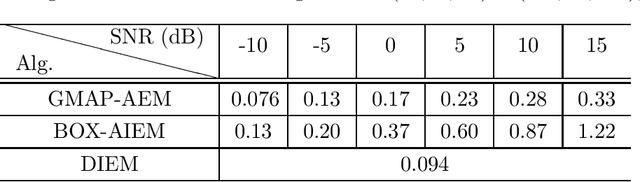
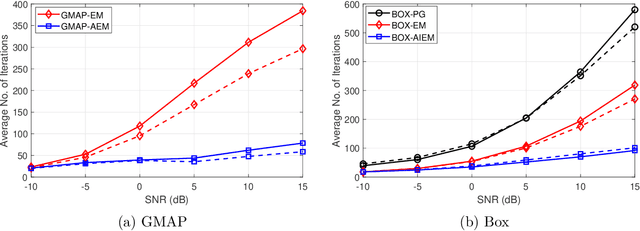
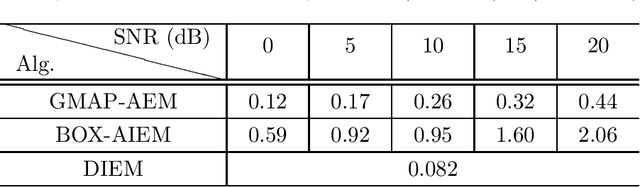
In this paper we study the expectation maximization (EM) technique for one-bit MIMO-OFDM detection (OMOD). Arising from the recent interest in massive MIMO with one-bit analog-to-digital converters, OMOD is a massive-scale problem. EM is an iterative method that can exploit the OFDM structure to process the problem in a per-iteration efficient fashion. In this study we analyze the convergence rate of EM for a class of approximate maximum-likelihood OMOD formulations, or, in a broader sense, a class of problems involving regression from quantized data. We show how the SNR and channel conditions can have an impact on the convergence rate. We do so by making a connection between the EM and the proximal gradient methods in the context of OMOD. This connection also gives us insight to build new accelerated and/or inexact EM schemes. The accelerated scheme has faster convergence in theory, and the inexact scheme provides us with the flexibility to implement EM more efficiently, with convergence guarantee. Furthermore we develop a deep EM algorithm, wherein we take the structure of our inexact EM algorithm and apply deep unfolding to train an efficient structured deep net. Simulation results show that our accelerated exact/inexact EM algorithms run much faster than their standard EM counterparts, and that the deep EM algorithm gives promising detection and runtime performances.

SISAL Revisited

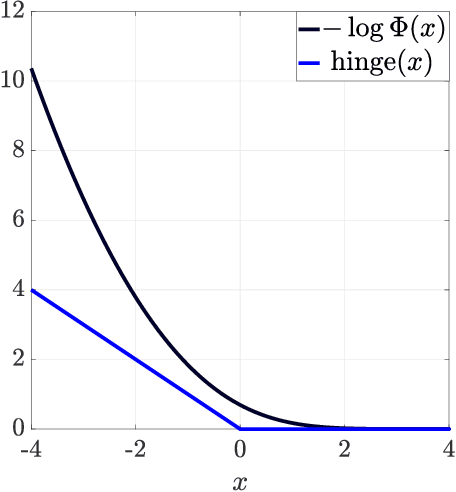
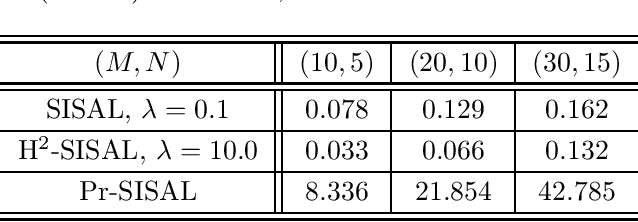
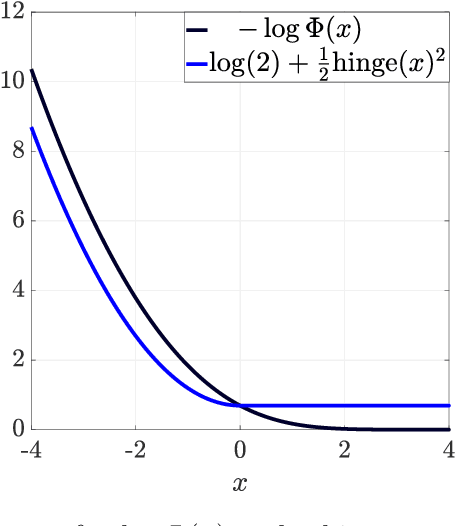
Simplex identification via split augmented Lagrangian (SISAL) is a popularly-used algorithm in blind unmixing of hyperspectral images. Developed by Jos\'{e} M. Bioucas-Dias in 2009, the algorithm is fundamentally relevant to tackling simplex-structured matrix factorization, and by extension, non-negative matrix factorization, which have many applications under their umbrellas. In this article, we revisit SISAL and provide new meanings to this quintessential algorithm. The formulation of SISAL was motivated from a geometric perspective, with no noise. We show that SISAL can be explained as a heuristic from a probabilistic simplex component analysis framework, which is statistical and is, by principle, more powerful in accommodating the presence of noise. The algorithm for SISAL was designed based on a successive convex approximation method, with a focus on practical utility. It was not known, by analyses, whether the SISAL algorithm has any kind of guarantee of convergence to a stationary point. By establishing associations between the SISAL algorithm and a line-search-based proximal gradient method, we confirm that SISAL can indeed guarantee convergence to a stationary point. Our re-explanation of SISAL also reveals new formulations and algorithms. The performance of these new possibilities is demonstrated by numerical experiments.

On Hyperspectral Unmixing

In this article the author reviews Jos\'e Bioucas-Dias' key contributions to hyperspectral unmixing (HU), in memory of him as an influential scholar and for his many beautiful ideas introduced to the hyperspectral community. Our story will start with vertex component analysis (VCA) -- one of the most celebrated HU algorithms, with more than 2,000 Google Scholar citations. VCA was pioneering, invented at a time when HU research just began to emerge, and it shows sharp insights on a then less-understood subject. Then we will turn to SISAL, another widely-used algorithm. SISAL is not only a highly successful algorithm, it is also a demonstration of its inventor's ingenuity on applied optimization and on smart formulation for practical noisy cases. Our tour will end with dependent component analysis (DECA), perhaps a less well-known contribution. DECA adopts a statistical inference framework, and the author's latest research indicates that such framework has great potential for further development, e.g., there are hidden connections between SISAL and DECA. The development of DECA shows foresight years ahead, in that regard.

Symbol-Level Precoding Through the Lens of Zero Forcing and Vector Perturbation

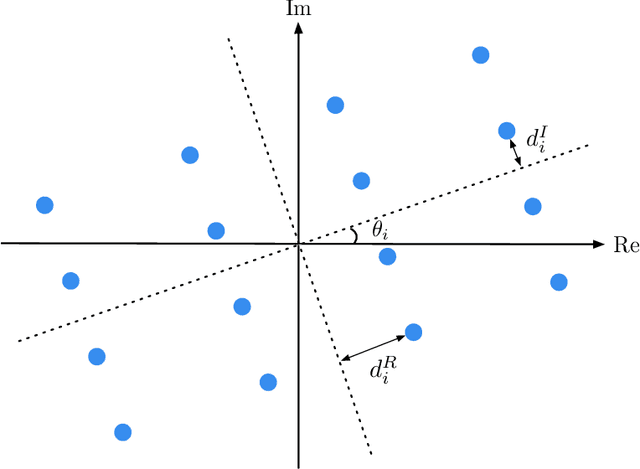
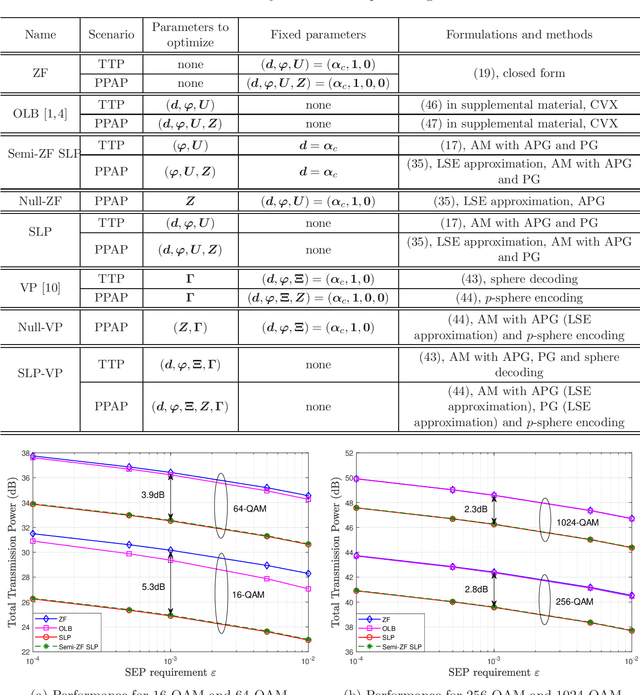
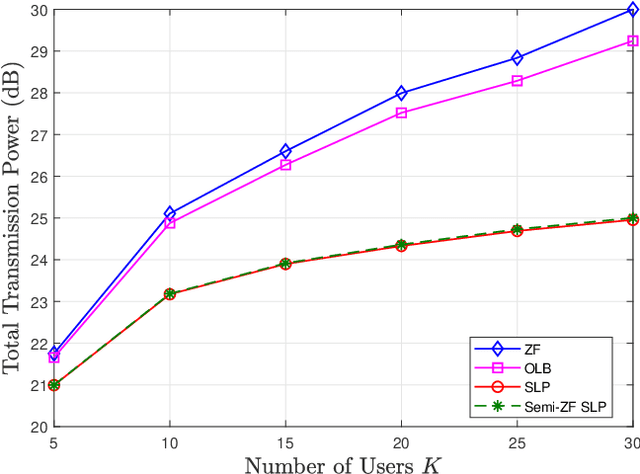
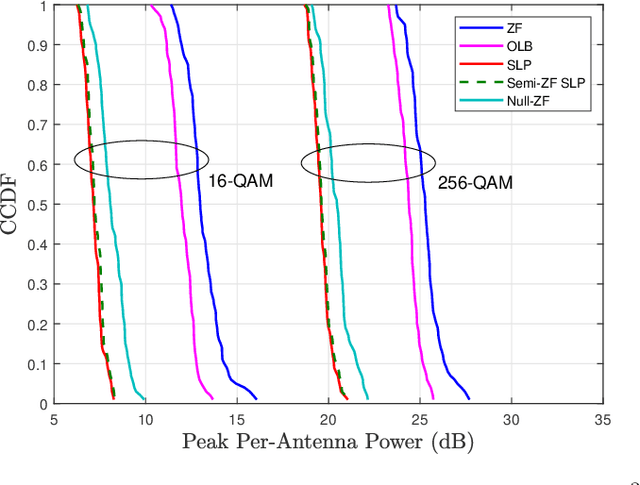
Symbol-level precoding (SLP) has recently emerged as a new paradigm for physical-layer transmit precoding in multiuser multi-input-multi-output (MIMO) channels. It exploits the underlying symbol constellation structure, which the conventional paradigm of linear precoding does not, to enhance symbol-level performance such as symbol error probability (SEP). It allows the precoder to take a more general form than linear precoding. This paper aims to better understand the relationships between SLP and linear precoding, subsequent design implications, and further connections beyond the existing SLP scope. Our study is built on a basic signal observation, namely, that SLP can be equivalently represented by a zero-forcing (ZF) linear precoding scheme augmented with some appropriately chosen symbol-dependent perturbation terms, and that some extended form of SLP is equivalent to a vector perturbation (VP) nonlinear precoding scheme augmented with the above-noted perturbation terms. We examine how insights arising from this perturbed ZF and VP interpretations can be leveraged to i) substantially simplify the optimization of certain SLP design criteria, namely, total or peak power minimization subject to SEP quality guarantees and under quadrature amplitude modulation (QAM) constellations; and ii) derive heuristic but computationally cheaper SLP designs. We also touch on the analysis side by showing that, under the total power minimization criterion, the basic ZF scheme is a near-optimal SLP scheme when the QAM order is very high--which gives a vital implication that SLP is more useful for lower-order QAM cases. Numerical results further indicate the merits and limitations of the different SLP designs derived from the perturbed ZF and VP interpretations.

Probabilistic Simplex Component Analysis

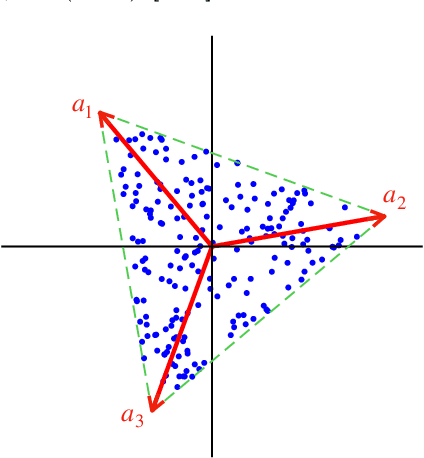
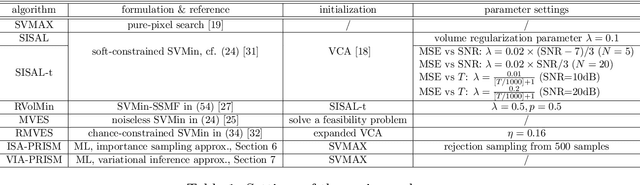
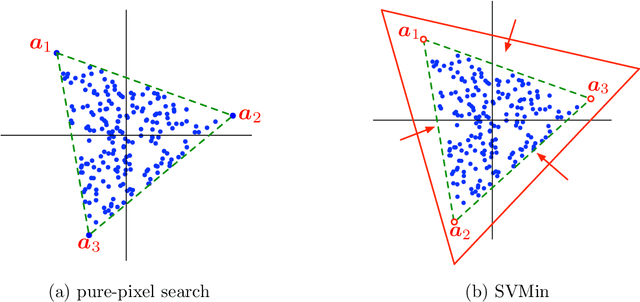
This study presents PRISM, a probabilistic simplex component analysis approach to identifying the vertices of a data-circumscribing simplex from data. The problem has a rich variety of applications, the most notable being hyperspectral unmixing in remote sensing and non-negative matrix factorization in machine learning. PRISM uses a simple probabilistic model, namely, uniform simplex data distribution and additive Gaussian noise, and it carries out inference by maximum likelihood. The inference model is sound in the sense that the vertices are provably identifiable under some assumptions, and it suggests that PRISM can be effective in combating noise when the number of data points is large. PRISM has strong, but hidden, relationships with simplex volume minimization, a powerful geometric approach for the same problem. We study these fundamental aspects, and we also consider algorithmic schemes based on importance sampling and variational inference. In particular, the variational inference scheme is shown to resemble a matrix factorization problem with a special regularizer, which draws an interesting connection to the matrix factorization approach. Numerical results are provided to demonstrate the potential of PRISM.

Understanding Notions of Stationarity in Non-Smooth Optimization

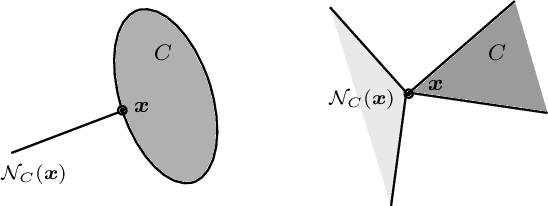
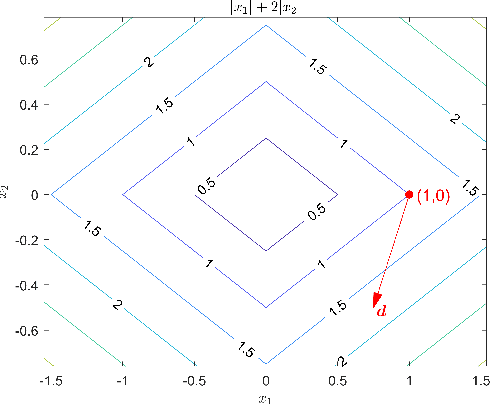
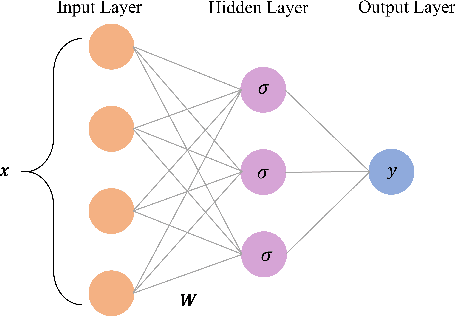
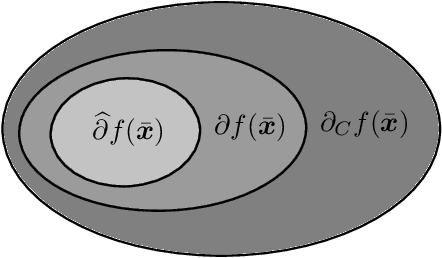
Many contemporary applications in signal processing and machine learning give rise to structured non-convex non-smooth optimization problems that can often be tackled by simple iterative methods quite effectively. One of the keys to understanding such a phenomenon---and, in fact, one of the very difficult conundrums even for experts---lie in the study of "stationary points" of the problem in question. Unlike smooth optimization, for which the definition of a stationary point is rather standard, there is a myriad of definitions of stationarity in non-smooth optimization. In this article, we give an introduction to different stationarity concepts for several important classes of non-convex non-smooth functions and discuss the geometric interpretations and further clarify the relationship among these different concepts. We then demonstrate the relevance of these constructions in some representative applications and how they could affect the performance of iterative methods for tackling these applications.

Hyperspectral Super-Resolution via Global-Local Low-Rank Matrix Estimation

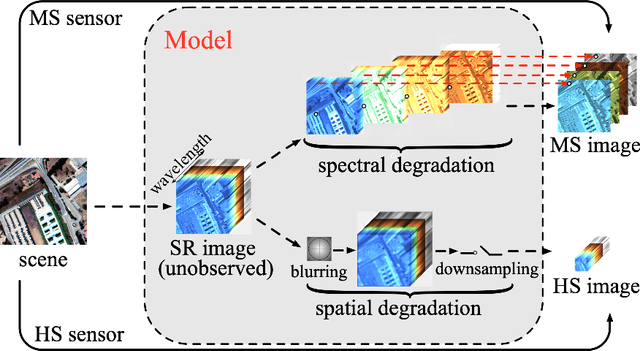
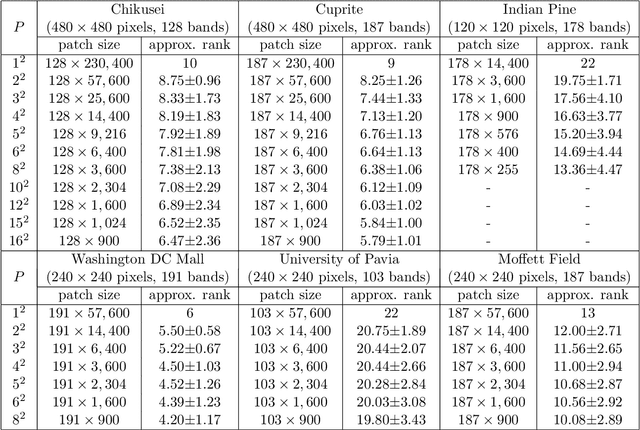
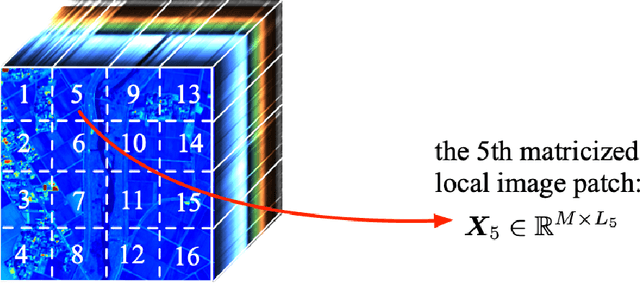
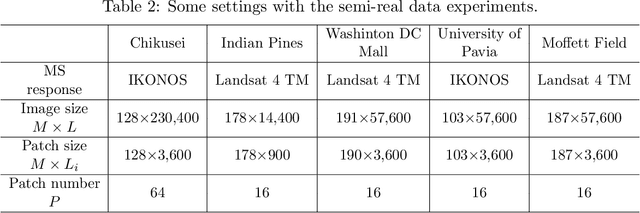
Hyperspectral super-resolution (HSR) is a problem that aims to estimate an image of high spectral and spatial resolutions from a pair of co-registered multispectral (MS) and hyperspectral (HS) images, which have coarser spectral and spatial resolutions, respectively. In this paper we pursue a low-rank matrix estimation approach for HSR. We assume that the spectral-spatial matrices associated with the whole image and the local areas of the image have low rank structures. The local low-rank assumption, in particular, has the aim of providing a more flexible model for accounting for local variation effects due to endmember variability. We formulate the HSR problem as a global-local rank-regularized least-squares problem. By leveraging on the recent advances in non-convex large-scale optimization, namely, the smooth Schatten-p approximation and the accelerated majorization-minimization method, we developed an efficient algorithm for the global-local low-rank problem. Numerical experiments on synthetic and semi-real data show that the proposed algorithm outperforms a number of benchmark algorithms in terms of recovery performance.

Nonnegative Matrix Factorization for Signal and Data Analytics: Identifiability, Algorithms, and Applications

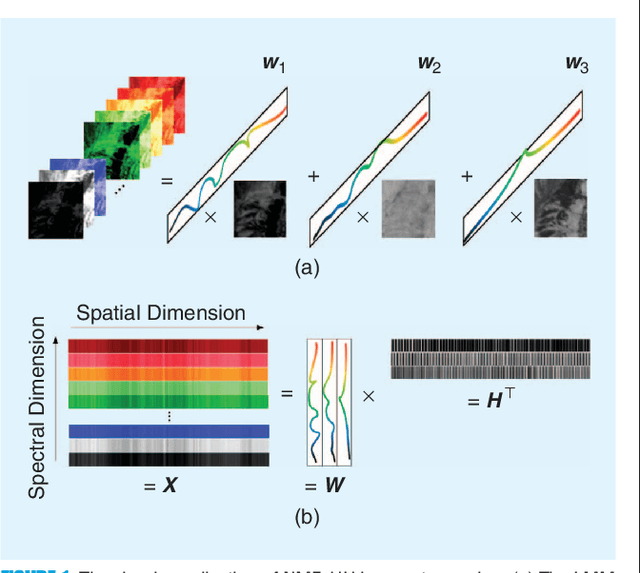
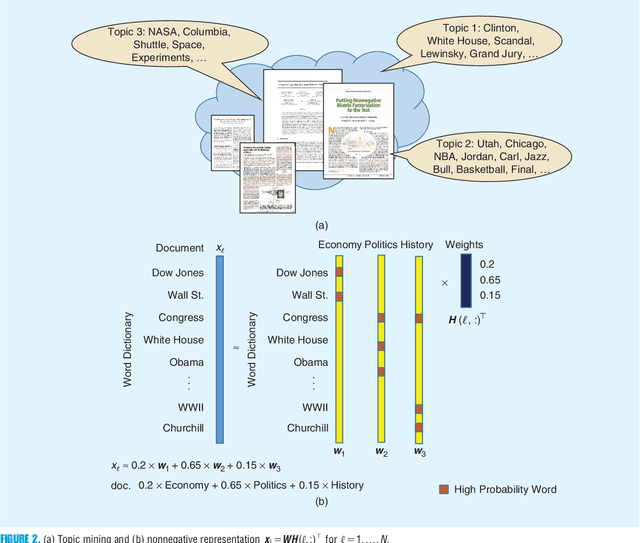
Nonnegative matrix factorization (NMF) has become a workhorse for signal and data analytics, triggered by its model parsimony and interpretability. Perhaps a bit surprisingly, the understanding to its model identifiability---the major reason behind the interpretability in many applications such as topic mining and hyperspectral imaging---had been rather limited until recent years. Beginning from the 2010s, the identifiability research of NMF has progressed considerably: Many interesting and important results have been discovered by the signal processing (SP) and machine learning (ML) communities. NMF identifiability has a great impact on many aspects in practice, such as ill-posed formulation avoidance and performance-guaranteed algorithm design. On the other hand, there is no tutorial paper that introduces NMF from an identifiability viewpoint. In this paper, we aim at filling this gap by offering a comprehensive and deep tutorial on model identifiability of NMF as well as the connections to algorithms and applications. This tutorial will help researchers and graduate students grasp the essence and insights of NMF, thereby avoiding typical `pitfalls' that are often times due to unidentifiable NMF formulations. This paper will also help practitioners pick/design suitable factorization tools for their own problems.