Why Machine Learning Models Fail to Fully Capture Epistemic Uncertainty

In recent years various supervised learning methods that disentangle aleatoric and epistemic uncertainty based on second-order distributions have been proposed. We argue that these methods fail to capture critical components of epistemic uncertainty, particularly due to the often-neglected component of model bias. To show this, we make use of a more fine-grained taxonomy of epistemic uncertainty sources in machine learning models, and analyse how the classical bias-variance decomposition of the expected prediction error can be decomposed into different parts reflecting these uncertainties. By using a simulation-based evaluation protocol which encompasses epistemic uncertainty due to both procedural- and data-driven uncertainty components, we illustrate that current methods rarely capture the full spectrum of epistemic uncertainty. Through theoretical insights and synthetic experiments, we show that high model bias can lead to misleadingly low estimates of epistemic uncertainty, and common second-order uncertainty quantification methods systematically blur bias-induced errors into aleatoric estimates, thereby underrepresenting epistemic uncertainty. Our findings underscore that meaningful aleatoric estimates are feasible only if all relevant sources of epistemic uncertainty are properly represented.

Optimal Conformal Prediction under Epistemic Uncertainty

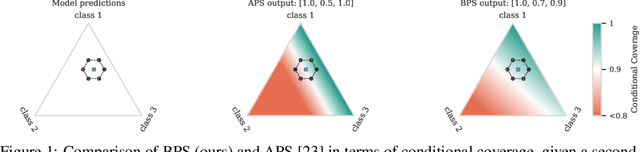
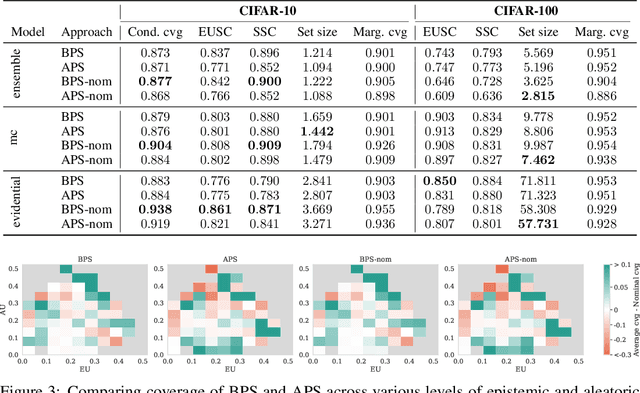
Conformal prediction (CP) is a popular frequentist framework for representing uncertainty by providing prediction sets that guarantee coverage of the true label with a user-adjustable probability. In most applications, CP operates on confidence scores coming from a standard (first-order) probabilistic predictor (e.g., softmax outputs). Second-order predictors, such as credal set predictors or Bayesian models, are also widely used for uncertainty quantification and are known for their ability to represent both aleatoric and epistemic uncertainty. Despite their popularity, there is still an open question on ``how they can be incorporated into CP''. In this paper, we discuss the desiderata for CP when valid second-order predictions are available. We then introduce Bernoulli prediction sets (BPS), which produce the smallest prediction sets that ensure conditional coverage in this setting. When given first-order predictions, BPS reduces to the well-known adaptive prediction sets (APS). Furthermore, when the validity assumption on the second-order predictions is compromised, we apply conformal risk control to obtain a marginal coverage guarantee while still accounting for epistemic uncertainty.

Conformal Prediction for Uncertainty Estimation in Drug-Target Interaction Prediction

Accurate drug-target interaction (DTI) prediction with machine learning models is essential for drug discovery. Such models should also provide a credible representation of their uncertainty, but applying classical marginal conformal prediction (CP) in DTI prediction often overlooks variability across drug and protein subgroups. In this work, we analyze three cluster-conditioned CP methods for DTI prediction, and compare them with marginal and group-conditioned CP. Clusterings are obtained via nonconformity scores, feature similarity, and nearest neighbors, respectively. Experiments on the KIBA dataset using four data-splitting strategies show that nonconformity-based clustering yields the tightest intervals and most reliable subgroup coverage, especially in random and fully unseen drug-protein splits. Group-conditioned CP works well when one entity is familiar, but residual-driven clustering provides robust uncertainty estimates even in sparse or novel scenarios. These results highlight the potential of cluster-based CP for improving DTI prediction under uncertainty.

A calibration test for evaluating set-based epistemic uncertainty representations

The accurate representation of epistemic uncertainty is a challenging yet essential task in machine learning. A widely used representation corresponds to convex sets of probabilistic predictors, also known as credal sets. One popular way of constructing these credal sets is via ensembling or specialized supervised learning methods, where the epistemic uncertainty can be quantified through measures such as the set size or the disagreement among members. In principle, these sets should contain the true data-generating distribution. As a necessary condition for this validity, we adopt the strongest notion of calibration as a proxy. Concretely, we propose a novel statistical test to determine whether there is a convex combination of the set's predictions that is calibrated in distribution. In contrast to previous methods, our framework allows the convex combination to be instance dependent, recognizing that different ensemble members may be better calibrated in different regions of the input space. Moreover, we learn this combination via proper scoring rules, which inherently optimize for calibration. Building on differentiable, kernel-based estimators of calibration errors, we introduce a nonparametric testing procedure and demonstrate the benefits of capturing instance-level variability on of synthetic and real-world experiments.

Conformal Prediction in Hierarchical Classification

Conformal prediction has emerged as a widely used framework for constructing valid prediction sets in classification and regression tasks. In this work, we extend the split conformal prediction framework to hierarchical classification, where prediction sets are commonly restricted to internal nodes of a predefined hierarchy, and propose two computationally efficient inference algorithms. The first algorithm returns internal nodes as prediction sets, while the second relaxes this restriction, using the notion of representation complexity, yielding a more general and combinatorial inference problem, but smaller set sizes. Empirical evaluations on several benchmark datasets demonstrate the effectiveness of the proposed algorithms in achieving nominal coverage.

Reducing Aleatoric and Epistemic Uncertainty through Multi-modal Data Acquisition

To generate accurate and reliable predictions, modern AI systems need to combine data from multiple modalities, such as text, images, audio, spreadsheets, and time series. Multi-modal data introduces new opportunities and challenges for disentangling uncertainty: it is commonly assumed in the machine learning community that epistemic uncertainty can be reduced by collecting more data, while aleatoric uncertainty is irreducible. However, this assumption is challenged in modern AI systems when information is obtained from different modalities. This paper introduces an innovative data acquisition framework where uncertainty disentanglement leads to actionable decisions, allowing sampling in two directions: sample size and data modality. The main hypothesis is that aleatoric uncertainty decreases as the number of modalities increases, while epistemic uncertainty decreases by collecting more observations. We provide proof-of-concept implementations on two multi-modal datasets to showcase our data acquisition framework, which combines ideas from active learning, active feature acquisition and uncertainty quantification.

Assessment of Uncertainty Quantification in Universal Differential Equations

Scientific Machine Learning is a new class of approaches that integrate physical knowledge and mechanistic models with data-driven techniques for uncovering governing equations of complex processes. Among the available approaches, Universal Differential Equations (UDEs) are used to combine prior knowledge in the form of mechanistic formulations with universal function approximators, like neural networks. Integral to the efficacy of UDEs is the joint estimation of parameters within mechanistic formulations and the universal function approximators using empirical data. The robustness and applicability of resultant models, however, hinge upon the rigorous quantification of uncertainties associated with these parameters, as well as the predictive capabilities of the overall model or its constituent components. With this work, we provide a formalisation of uncertainty quantification (UQ) for UDEs and investigate important frequentist and Bayesian methods. By analysing three synthetic examples of varying complexity, we evaluate the validity and efficiency of ensembles, variational inference and Markov chain Monte Carlo sampling as epistemic UQ methods for UDEs.

Is Epistemic Uncertainty Faithfully Represented by Evidential Deep Learning Methods?

Trustworthy ML systems should not only return accurate predictions, but also a reliable representation of their uncertainty. Bayesian methods are commonly used to quantify both aleatoric and epistemic uncertainty, but alternative approaches, such as evidential deep learning methods, have become popular in recent years. The latter group of methods in essence extends empirical risk minimization (ERM) for predicting second-order probability distributions over outcomes, from which measures of epistemic (and aleatoric) uncertainty can be extracted. This paper presents novel theoretical insights of evidential deep learning, highlighting the difficulties in optimizing second-order loss functions and interpreting the resulting epistemic uncertainty measures. With a systematic setup that covers a wide range of approaches for classification, regression and counts, it provides novel insights into issues of identifiability and convergence in second-order loss minimization, and the relative (rather than absolute) nature of epistemic uncertainty measures.

Heteroskedastic conformal regression

Conformal prediction, and split conformal prediction as a specific implementation, offer a distribution-free approach to estimating prediction intervals with statistical guarantees. Recent work has shown that split conformal prediction can produce state-of-the-art prediction intervals when focusing on marginal coverage, i.e., on a calibration dataset the method produces on average prediction intervals that contain the ground truth with a predefined coverage level. However, such intervals are often not adaptive, which can be problematic for regression problems with heteroskedastic noise. This paper tries to shed new light on how adaptive prediction intervals can be constructed using methods such as normalized and Mondrian conformal prediction. We present theoretical and experimental results in which these methods are investigated in a systematic way.

The out-of-sample $R^2$: estimation and inference

Out-of-sample prediction is the acid test of predictive models, yet an independent test dataset is often not available for assessment of the prediction error. For this reason, out-of-sample performance is commonly estimated using data splitting algorithms such as cross-validation or the bootstrap. For quantitative outcomes, the ratio of variance explained to total variance can be summarized by the coefficient of determination or in-sample $R^2$, which is easy to interpret and to compare across different outcome variables. As opposed to the in-sample $R^2$, the out-of-sample $R^2$ has not been well defined and the variability on the out-of-sample $\hat{R}^2$ has been largely ignored. Usually only its point estimate is reported, hampering formal comparison of predictability of different outcome variables. Here we explicitly define the out-of-sample $R^2$ as a comparison of two predictive models, provide an unbiased estimator and exploit recent theoretical advances on uncertainty of data splitting estimates to provide a standard error for the $\hat{R}^2$. The performance of the estimators for the $R^2$ and its standard error are investigated in a simulation study. We demonstrate our new method by constructing confidence intervals and comparing models for prediction of quantitative $\text{Brassica napus}$ and $\text{Zea mays}$ phenotypes based on gene expression data.