Learning to Defer in Content Moderation: The Human-AI Interplay

Successful content moderation in online platforms relies on a human-AI collaboration approach. A typical heuristic estimates the expected harmfulness of a post and uses fixed thresholds to decide whether to remove it and whether to send it for human review. This disregards the prediction uncertainty, the time-varying element of human review capacity and post arrivals, and the selective sampling in the dataset (humans only review posts filtered by the admission algorithm). In this paper, we introduce a model to capture the human-AI interplay in content moderation. The algorithm observes contextual information for incoming posts, makes classification and admission decisions, and schedules posts for human review. Only admitted posts receive human reviews on their harmfulness. These reviews help educate the machine-learning algorithms but are delayed due to congestion in the human review system. The classical learning-theoretic way to capture this human-AI interplay is via the framework of learning to defer, where the algorithm has the option to defer a classification task to humans for a fixed cost and immediately receive feedback. Our model contributes to this literature by introducing congestion in the human review system. Moreover, unlike work on online learning with delayed feedback where the delay in the feedback is exogenous to the algorithm's decisions, the delay in our model is endogenous to both the admission and the scheduling decisions. We propose a near-optimal learning algorithm that carefully balances the classification loss from a selectively sampled dataset, the idiosyncratic loss of non-reviewed posts, and the delay loss of having congestion in the human review system. To the best of our knowledge, this is the first result for online learning in contextual queueing systems and hence our analytical framework may be of independent interest.

Quantifying the Cost of Learning in Queueing Systems

Queueing systems are widely applicable stochastic models with use cases in communication networks, healthcare, service systems, etc. Although their optimal control has been extensively studied, most existing approaches assume perfect knowledge of system parameters. Of course, this assumption rarely holds in practice where there is parameter uncertainty, thus motivating a recent line of work on bandit learning for queueing systems. This nascent stream of research focuses on the asymptotic performance of the proposed algorithms. In this paper, we argue that an asymptotic metric, which focuses on late-stage performance, is insufficient to capture the intrinsic statistical complexity of learning in queueing systems which typically occurs in the early stage. Instead, we propose the Cost of Learning in Queueing (CLQ), a new metric that quantifies the maximum increase in time-averaged queue length caused by parameter uncertainty. We characterize the CLQ of a single-queue multi-server system, and then extend these results to multi-queue multi-server systems and networks of queues. In establishing our results, we propose a unified analysis framework for CLQ that bridges Lyapunov and bandit analysis, which could be of independent interest.

Efficient decentralized multi-agent learning in asymmetric queuing systems

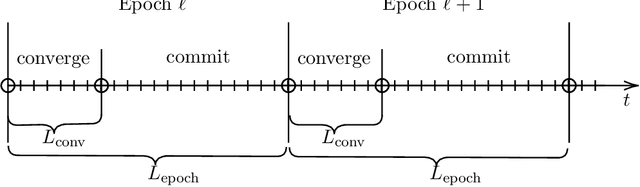
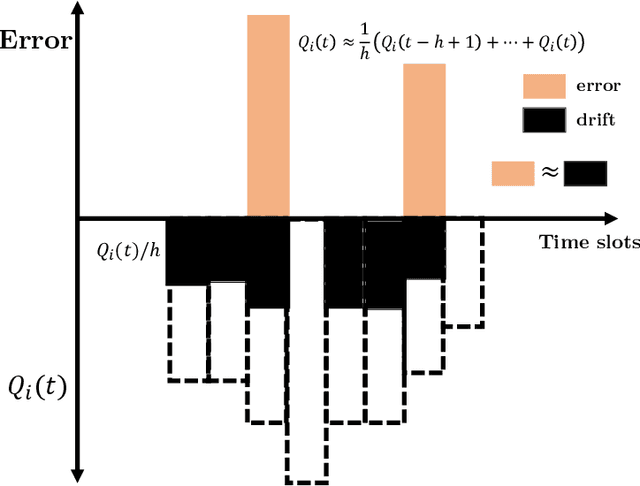
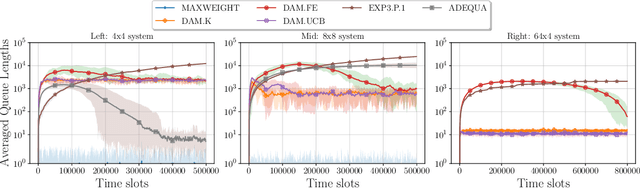
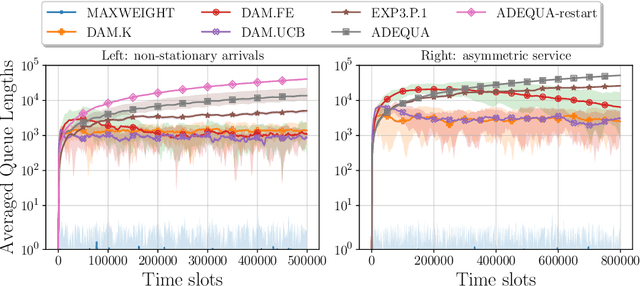
We study decentralized multi-agent learning in bipartite queuing systems, a standard model for service systems. In particular, $N$ agents request service from $K$ servers in a fully decentralized way, i.e, by running the same algorithm without communication. Previous decentralized algorithms are restricted to symmetric systems, have performance that is degrading exponentially in the number of servers, require communication through shared randomness and unique agent identities, and are computationally demanding. In contrast, we provide a simple learning algorithm that, when run decentrally by each agent, leads the queuing system to have efficient performance in general asymmetric bipartite queuing systems while also having additional robustness properties. Along the way, we provide the first UCB-based algorithm for the centralized case of the problem, which resolves an open question by Krishnasamy et al. (2016,2021).

Provably-Efficient Double Q-Learning

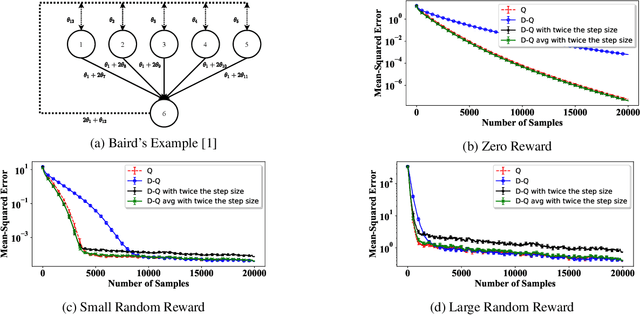
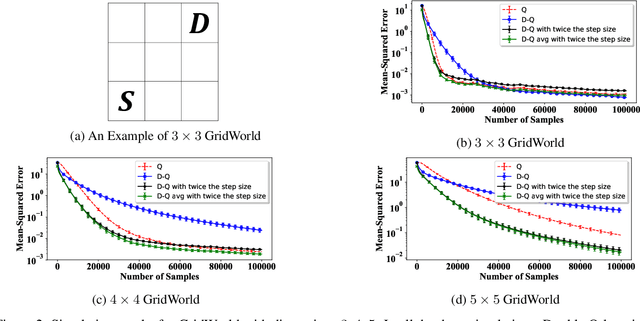
In this paper, we establish a theoretical comparison between the asymptotic mean-squared error of Double Q-learning and Q-learning. Our result builds upon an analysis for linear stochastic approximation based on Lyapunov equations and applies to both tabular setting and with linear function approximation, provided that the optimal policy is unique and the algorithms converge. We show that the asymptotic mean-squared error of Double Q-learning is exactly equal to that of Q-learning if Double Q-learning uses twice the learning rate of Q-learning and outputs the average of its two estimators. We also present some practical implications of this theoretical observation using simulations.