Design of experiments for the calibration of history-dependent models via deep reinforcement learning and an enhanced Kalman filter

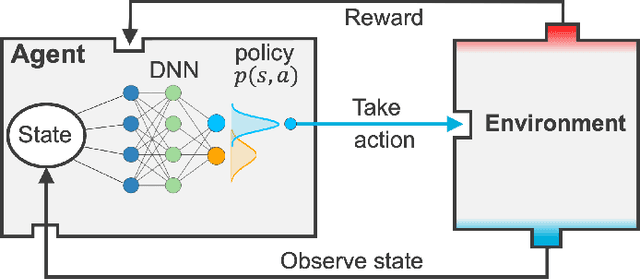
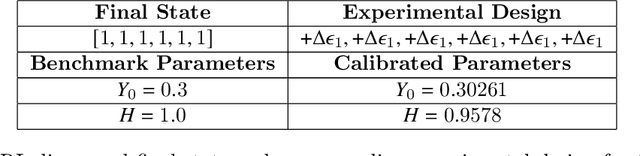
Experimental data is costly to obtain, which makes it difficult to calibrate complex models. For many models an experimental design that produces the best calibration given a limited experimental budget is not obvious. This paper introduces a deep reinforcement learning (RL) algorithm for design of experiments that maximizes the information gain measured by Kullback-Leibler (KL) divergence obtained via the Kalman filter (KF). This combination enables experimental design for rapid online experiments where traditional methods are too costly. We formulate possible configurations of experiments as a decision tree and a Markov decision process (MDP), where a finite choice of actions is available at each incremental step. Once an action is taken, a variety of measurements are used to update the state of the experiment. This new data leads to a Bayesian update of the parameters by the KF, which is used to enhance the state representation. In contrast to the Nash-Sutcliffe efficiency (NSE) index, which requires additional sampling to test hypotheses for forward predictions, the KF can lower the cost of experiments by directly estimating the values of new data acquired through additional actions. In this work our applications focus on mechanical testing of materials. Numerical experiments with complex, history-dependent models are used to verify the implementation and benchmark the performance of the RL-designed experiments.

Machine learning structure preserving brackets for forecasting irreversible processes

Forecasting of time-series data requires imposition of inductive biases to obtain predictive extrapolation, and recent works have imposed Hamiltonian/Lagrangian form to preserve structure for systems with reversible dynamics. In this work we present a novel parameterization of dissipative brackets from metriplectic dynamical systems appropriate for learning irreversible dynamics with unknown a priori model form. The process learns generalized Casimirs for energy and entropy guaranteed to be conserved and nondecreasing, respectively. Furthermore, for the case of added thermal noise, we guarantee exact preservation of a fluctuation-dissipation theorem, ensuring thermodynamic consistency. We provide benchmarks for dissipative systems demonstrating learned dynamics are more robust and generalize better than either "black-box" or penalty-based approaches.

Partition of unity networks: deep hp-approximation

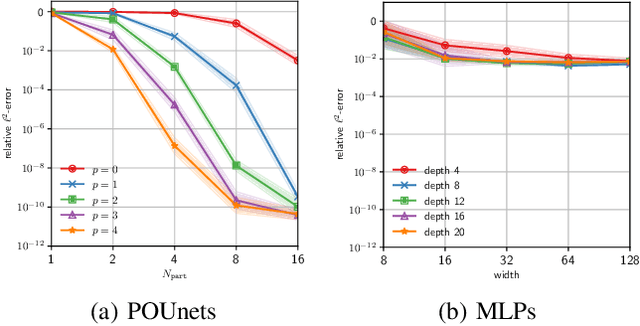
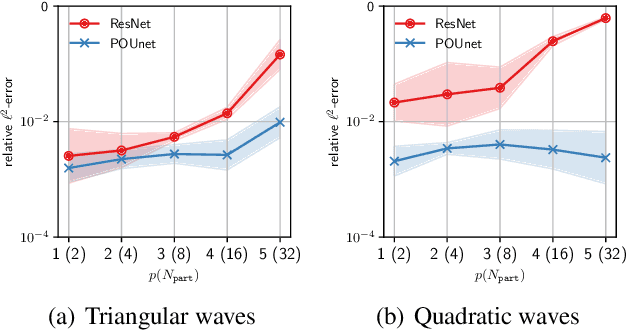
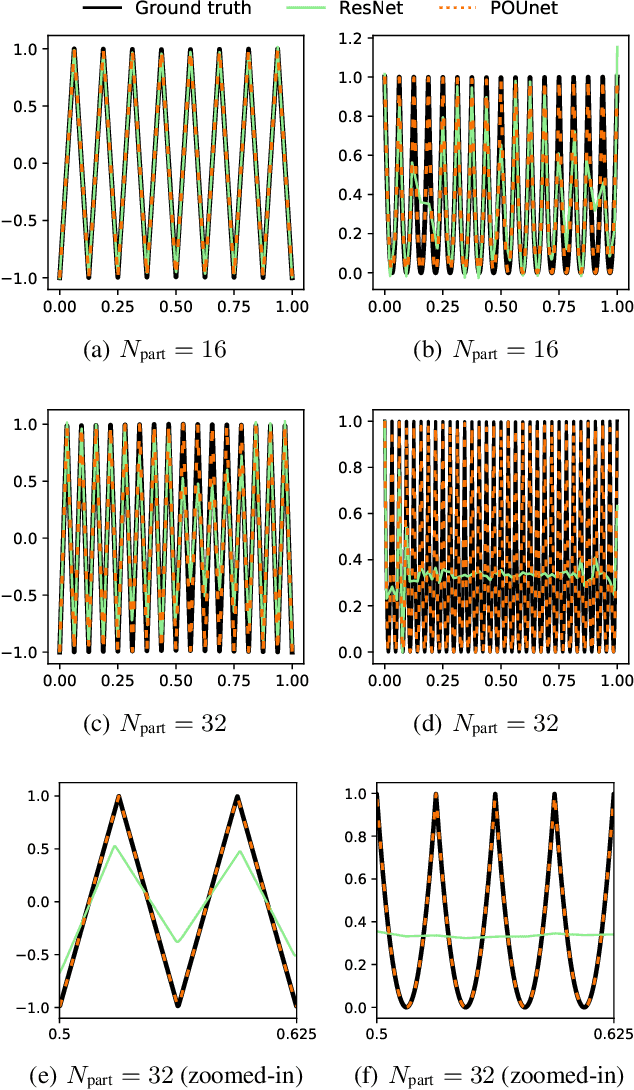
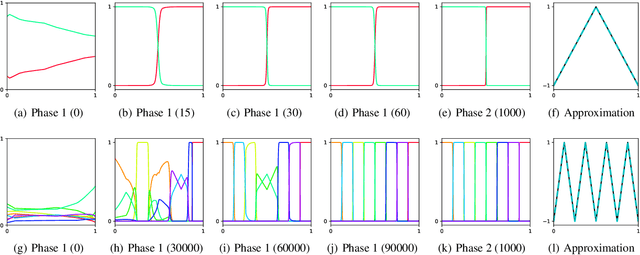
Approximation theorists have established best-in-class optimal approximation rates of deep neural networks by utilizing their ability to simultaneously emulate partitions of unity and monomials. Motivated by this, we propose partition of unity networks (POUnets) which incorporate these elements directly into the architecture. Classification architectures of the type used to learn probability measures are used to build a meshfree partition of space, while polynomial spaces with learnable coefficients are associated to each partition. The resulting hp-element-like approximation allows use of a fast least-squares optimizer, and the resulting architecture size need not scale exponentially with spatial dimension, breaking the curse of dimensionality. An abstract approximation result establishes desirable properties to guide network design. Numerical results for two choices of architecture demonstrate that POUnets yield hp-convergence for smooth functions and consistently outperform MLPs for piecewise polynomial functions with large numbers of discontinuities.

A physics-informed operator regression framework for extracting data-driven continuum models

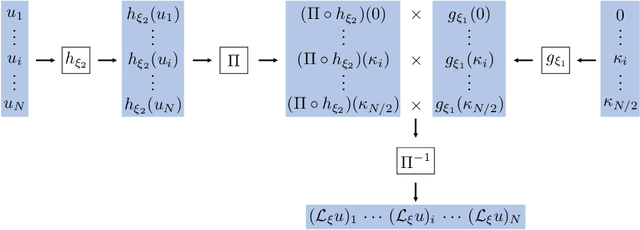
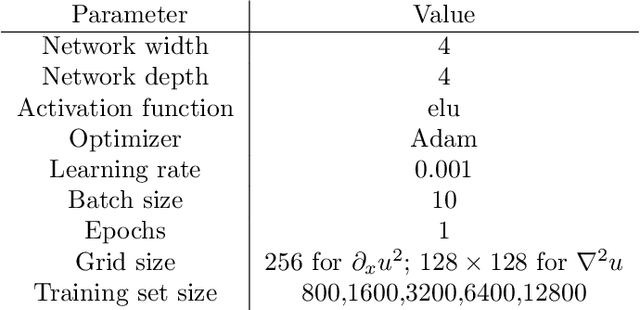
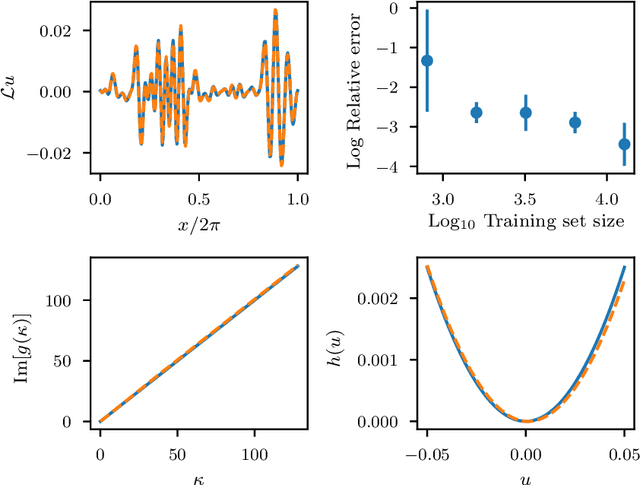
The application of deep learning toward discovery of data-driven models requires careful application of inductive biases to obtain a description of physics which is both accurate and robust. We present here a framework for discovering continuum models from high fidelity molecular simulation data. Our approach applies a neural network parameterization of governing physics in modal space, allowing a characterization of differential operators while providing structure which may be used to impose biases related to symmetry, isotropy, and conservation form. We demonstrate the effectiveness of our framework for a variety of physics, including local and nonlocal diffusion processes and single and multiphase flows. For the flow physics we demonstrate this approach leads to a learned operator that generalizes to system characteristics not included in the training sets, such as variable particle sizes, densities, and concentration.

A block coordinate descent optimizer for classification problems exploiting convexity

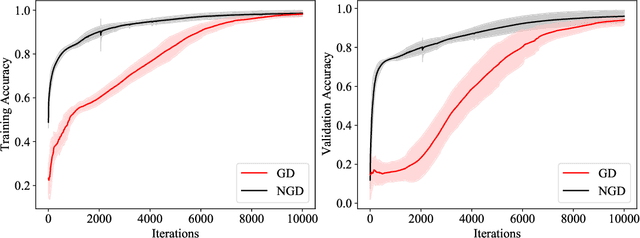
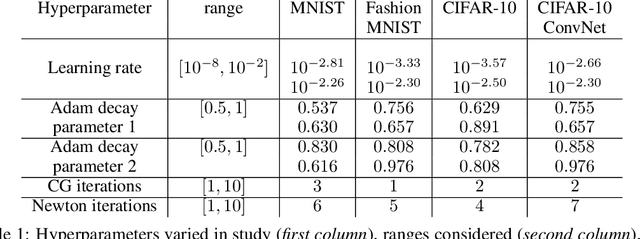
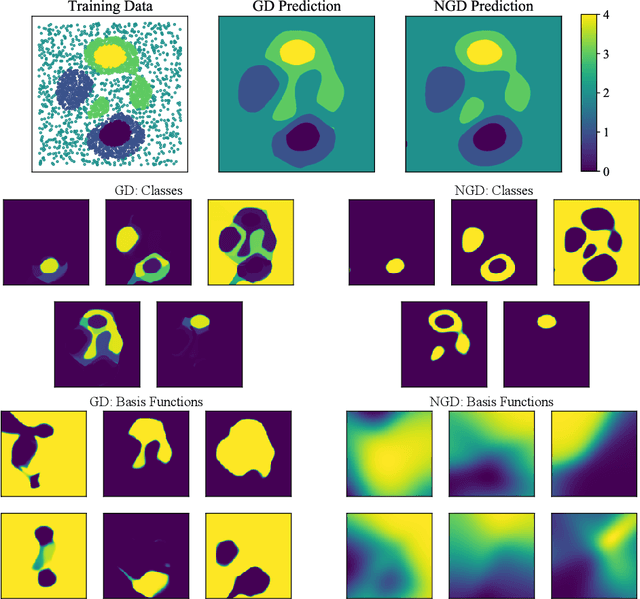
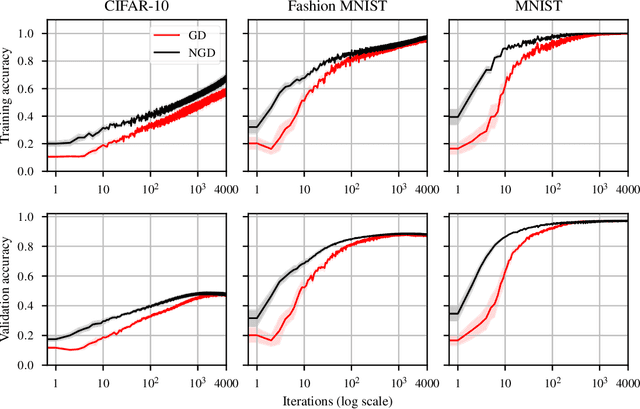
Second-order optimizers hold intriguing potential for deep learning, but suffer from increased cost and sensitivity to the non-convexity of the loss surface as compared to gradient-based approaches. We introduce a coordinate descent method to train deep neural networks for classification tasks that exploits global convexity of the cross-entropy loss in the weights of the linear layer. Our hybrid Newton/Gradient Descent (NGD) method is consistent with the interpretation of hidden layers as providing an adaptive basis and the linear layer as providing an optimal fit of the basis to data. By alternating between a second-order method to find globally optimal parameters for the linear layer and gradient descent to train the hidden layers, we ensure an optimal fit of the adaptive basis to data throughout training. The size of the Hessian in the second-order step scales only with the number weights in the linear layer and not the depth and width of the hidden layers; furthermore, the approach is applicable to arbitrary hidden layer architecture. Previous work applying this adaptive basis perspective to regression problems demonstrated significant improvements in accuracy at reduced training cost, and this work can be viewed as an extension of this approach to classification problems. We first prove that the resulting Hessian matrix is symmetric semi-definite, and that the Newton step realizes a global minimizer. By studying classification of manufactured two-dimensional point cloud data, we demonstrate both an improvement in validation error and a striking qualitative difference in the basis functions encoded in the hidden layer when trained using NGD. Application to image classification benchmarks for both dense and convolutional architectures reveals improved training accuracy, suggesting possible gains of second-order methods over gradient descent.

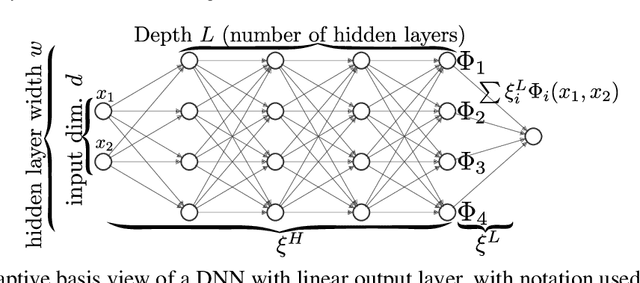
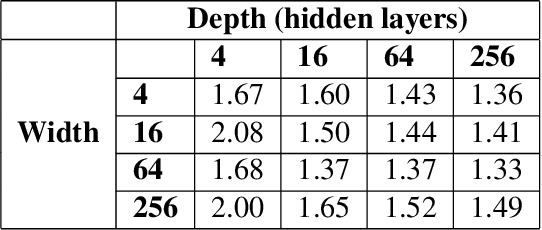
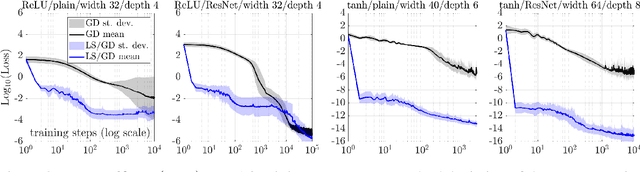
Robust Training and Initialization of Deep Neural Networks: An Adaptive Basis Viewpoint

Motivated by the gap between theoretical optimal approximation rates of deep neural networks (DNNs) and the accuracy realized in practice, we seek to improve the training of DNNs. The adoption of an adaptive basis viewpoint of DNNs leads to novel initializations and a hybrid least squares/gradient descent optimizer. We provide analysis of these techniques and illustrate via numerical examples dramatic increases in accuracy and convergence rate for benchmarks characterizing scientific applications where DNNs are currently used, including regression problems and physics-informed neural networks for the solution of partial differential equations.