Graph Persistence goes Spectral

Including intricate topological information (e.g., cycles) provably enhances the expressivity of message-passing graph neural networks (GNNs) beyond the Weisfeiler-Leman (WL) hierarchy. Consequently, Persistent Homology (PH) methods are increasingly employed for graph representation learning. In this context, recent works have proposed decorating classical PH diagrams with vertex and edge features for improved expressivity. However, due to their dependence on features, these methods still fail to capture basic graph structural information. In this paper, we propose SpectRe -- a new topological descriptor for graphs that integrates spectral information into PH diagrams. Notably, SpectRe is strictly more expressive than existing descriptors on graphs. We also introduce notions of global and local stability to analyze existing descriptors and establish that SpectRe is locally stable. Finally, experiments on synthetic and real-world datasets demonstrate the effectiveness of SpectRe and its potential to enhance the capabilities of graph models in relevant learning tasks.

Positional Encoding meets Persistent Homology on Graphs

The local inductive bias of message-passing graph neural networks (GNNs) hampers their ability to exploit key structural information (e.g., connectivity and cycles). Positional encoding (PE) and Persistent Homology (PH) have emerged as two promising approaches to mitigate this issue. PE schemes endow GNNs with location-aware features, while PH methods enhance GNNs with multiresolution topological features. However, a rigorous theoretical characterization of the relative merits and shortcomings of PE and PH has remained elusive. We bridge this gap by establishing that neither paradigm is more expressive than the other, providing novel constructions where one approach fails but the other succeeds. Our insights inform the design of a novel learnable method, PiPE (Persistence-informed Positional Encoding), which is provably more expressive than both PH and PE. PiPE demonstrates strong performance across a variety of tasks (e.g., molecule property prediction, graph classification, and out-of-distribution generalization), thereby advancing the frontiers of graph representation learning. Code is available at https://github.com/Aalto-QuML/PIPE.

Going beyond persistent homology using persistent homology

Representational limits of message-passing graph neural networks (MP-GNNs), e.g., in terms of the Weisfeiler-Leman (WL) test for isomorphism, are well understood. Augmenting these graph models with topological features via persistent homology (PH) has gained prominence, but identifying the class of attributed graphs that PH can recognize remains open. We introduce a novel concept of color-separating sets to provide a complete resolution to this important problem. Specifically, we establish the necessary and sufficient conditions for distinguishing graphs based on the persistence of their connected components, obtained from filter functions on vertex and edge colors. Our constructions expose the limits of vertex- and edge-level PH, proving that neither category subsumes the other. Leveraging these theoretical insights, we propose RePHINE for learning topological features on graphs. RePHINE efficiently combines vertex- and edge-level PH, achieving a scheme that is provably more powerful than both. Integrating RePHINE into MP-GNNs boosts their expressive power, resulting in gains over standard PH on several benchmarks for graph classification.

Provably expressive temporal graph networks

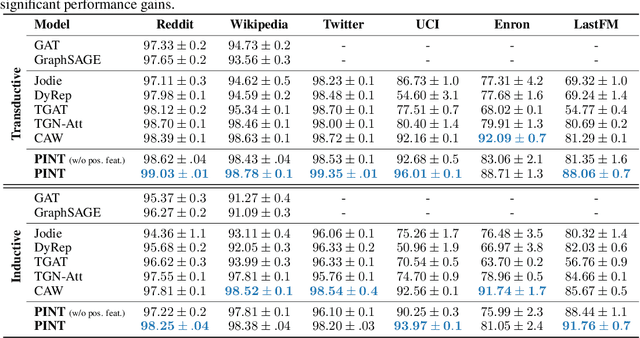
Temporal graph networks (TGNs) have gained prominence as models for embedding dynamic interactions, but little is known about their theoretical underpinnings. We establish fundamental results about the representational power and limits of the two main categories of TGNs: those that aggregate temporal walks (WA-TGNs), and those that augment local message passing with recurrent memory modules (MP-TGNs). Specifically, novel constructions reveal the inadequacy of MP-TGNs and WA-TGNs, proving that neither category subsumes the other. We extend the 1-WL (Weisfeiler-Leman) test to temporal graphs, and show that the most powerful MP-TGNs should use injective updates, as in this case they become as expressive as the temporal WL. Also, we show that sufficiently deep MP-TGNs cannot benefit from memory, and MP/WA-TGNs fail to compute graph properties such as girth. These theoretical insights lead us to PINT -- a novel architecture that leverages injective temporal message passing and relative positional features. Importantly, PINT is provably more expressive than both MP-TGNs and WA-TGNs. PINT significantly outperforms existing TGNs on several real-world benchmarks.

Rethinking pooling in graph neural networks

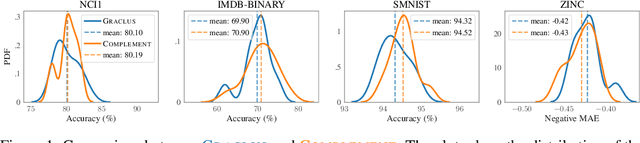
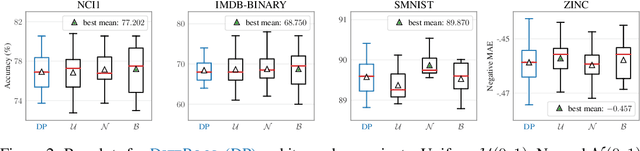
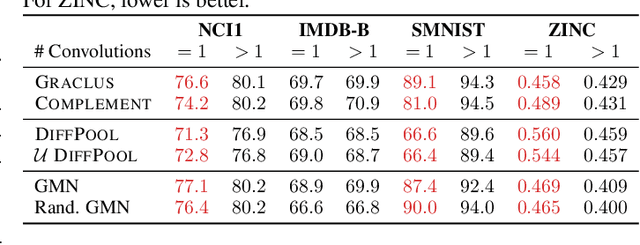
Graph pooling is a central component of a myriad of graph neural network (GNN) architectures. As an inheritance from traditional CNNs, most approaches formulate graph pooling as a cluster assignment problem, extending the idea of local patches in regular grids to graphs. Despite the wide adherence to this design choice, no work has rigorously evaluated its influence on the success of GNNs. In this paper, we build upon representative GNNs and introduce variants that challenge the need for locality-preserving representations, either using randomization or clustering on the complement graph. Strikingly, our experiments demonstrate that using these variants does not result in any decrease in performance. To understand this phenomenon, we study the interplay between convolutional layers and the subsequent pooling ones. We show that the convolutions play a leading role in the learned representations. In contrast to the common belief, local pooling is not responsible for the success of GNNs on relevant and widely-used benchmarks.