Are Deep Learning Based Hybrid PDE Solvers Reliable? Why Training Paradigms and Update Strategies Matter

Deep learning-based hybrid iterative methods (DL-HIMs) integrate classical numerical solvers with neural operators, utilizing their complementary spectral biases to accelerate convergence. Despite this promise, many DL-HIMs stagnate at false fixed points where neural updates vanish while the physical residual remains large, raising questions about reliability in scientific computing. In this paper, we provide evidence that performance is highly sensitive to training paradigms and update strategies, even when the neural architecture is fixed. Through a detailed study of a DeepONet-based hybrid iterative numerical transferable solver (HINTS) and an FFT-based Fourier neural solver (FNS), we show that significant physical residuals can persist when training objectives are not aligned with solver dynamics and problem physics. We further examine Anderson acceleration (AA) and demonstrate that its classical form is ill-suited for nonlinear neural operators. To overcome this, we introduce physics-aware Anderson acceleration (PA-AA), which minimizes the physical residual rather than the fixed-point update. Numerical experiments confirm that PA-AA restores reliable convergence in substantially fewer iterations. These findings provide a concrete answer to ongoing controversies surrounding AI-based PDE solvers: reliability hinges not only on architectures but on physically informed training and iteration design.

Neural network-driven domain decomposition for efficient solutions to the Helmholtz equation

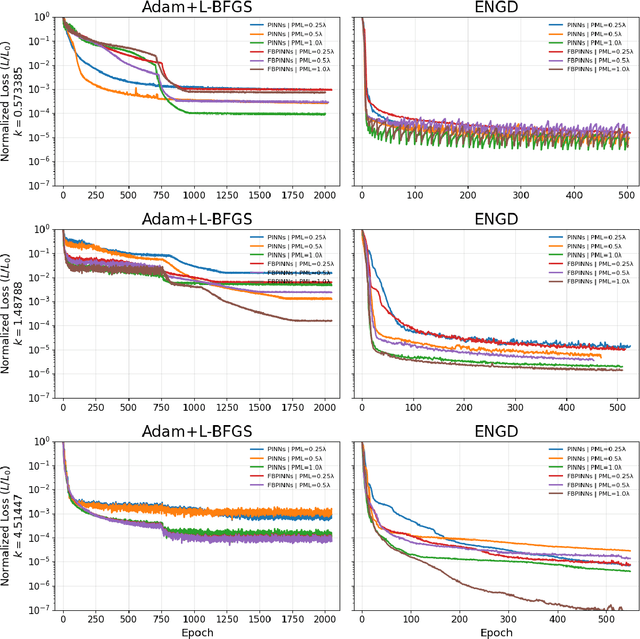
Accurately simulating wave propagation is crucial in fields such as acoustics, electromagnetism, and seismic analysis. Traditional numerical methods, like finite difference and finite element approaches, are widely used to solve governing partial differential equations (PDEs) such as the Helmholtz equation. However, these methods face significant computational challenges when applied to high-frequency wave problems in complex two-dimensional domains. This work investigates Finite Basis Physics-Informed Neural Networks (FBPINNs) and their multilevel extensions as a promising alternative. These methods leverage domain decomposition, partitioning the computational domain into overlapping sub-domains, each governed by a local neural network. We assess their accuracy and computational efficiency in solving the Helmholtz equation for the homogeneous case, demonstrating their potential to mitigate the limitations of traditional approaches.

Two-level deep domain decomposition method

This study presents a two-level Deep Domain Decomposition Method (Deep-DDM) augmented with a coarse-level network for solving boundary value problems using physics-informed neural networks (PINNs). The addition of the coarse level network improves scalability and convergence rates compared to the single level method. Tested on a Poisson equation with Dirichlet boundary conditions, the two-level deep DDM demonstrates superior performance, maintaining efficient convergence regardless of the number of subdomains. This advance provides a more scalable and effective approach to solving complex partial differential equations with machine learning.