Neural network-driven domain decomposition for efficient solutions to the Helmholtz equation

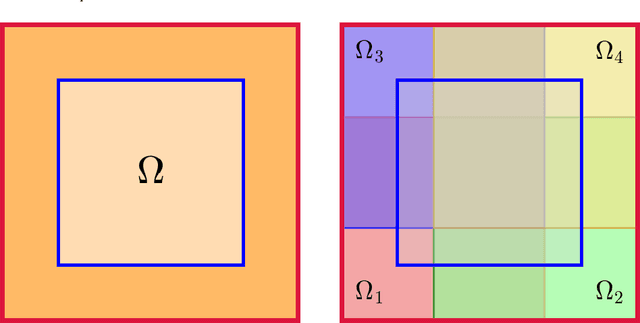
Accurately simulating wave propagation is crucial in fields such as acoustics, electromagnetism, and seismic analysis. Traditional numerical methods, like finite difference and finite element approaches, are widely used to solve governing partial differential equations (PDEs) such as the Helmholtz equation. However, these methods face significant computational challenges when applied to high-frequency wave problems in complex two-dimensional domains. This work investigates Finite Basis Physics-Informed Neural Networks (FBPINNs) and their multilevel extensions as a promising alternative. These methods leverage domain decomposition, partitioning the computational domain into overlapping sub-domains, each governed by a local neural network. We assess their accuracy and computational efficiency in solving the Helmholtz equation for the homogeneous case, demonstrating their potential to mitigate the limitations of traditional approaches.

BO-SA-PINNs: Self-adaptive physics-informed neural networks based on Bayesian optimization for automatically designing PDE solvers

Physics-informed neural networks (PINNs) is becoming a popular alternative method for solving partial differential equations (PDEs). However, they require dedicated manual modifications to the hyperparameters of the network, the sampling methods and loss function weights for different PDEs, which reduces the efficiency of the solvers. In this paper, we pro- pose a general multi-stage framework, i.e. BO-SA-PINNs to alleviate this issue. In the first stage, Bayesian optimization (BO) is used to select hyperparameters for the training process, and based on the results of the pre-training, the network architecture, learning rate, sampling points distribution and loss function weights suitable for the PDEs are automatically determined. The proposed hyperparameters search space based on experimental results can enhance the efficiency of BO in identifying optimal hyperparameters. After selecting the appropriate hyperparameters, we incorporate a global self-adaptive (SA) mechanism the second stage. Using the pre-trained model and loss information in the second-stage training, the exponential moving average (EMA) method is employed to optimize the loss function weights, and residual-based adaptive refinement with distribution (RAR-D) is used to optimize the sampling points distribution. In the third stage, L-BFGS is used for stable training. In addition, we introduce a new activation function that enables BO-SA-PINNs to achieve higher accuracy. In numerical experiments, we conduct comparative and ablation experiments to verify the performance of the model on Helmholtz, Maxwell, Burgers and high-dimensional Poisson equations. The comparative experiment results show that our model can achieve higher accuracy and fewer iterations in test cases, and the ablation experiments demonstrate the positive impact of every improvement.