Neural network-driven domain decomposition for efficient solutions to the Helmholtz equation

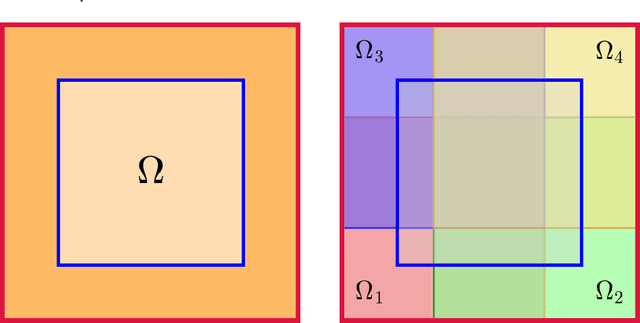
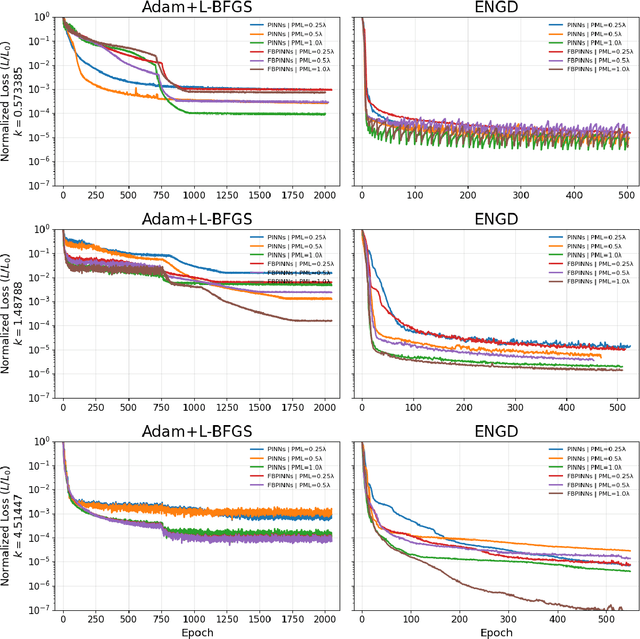
Accurately simulating wave propagation is crucial in fields such as acoustics, electromagnetism, and seismic analysis. Traditional numerical methods, like finite difference and finite element approaches, are widely used to solve governing partial differential equations (PDEs) such as the Helmholtz equation. However, these methods face significant computational challenges when applied to high-frequency wave problems in complex two-dimensional domains. This work investigates Finite Basis Physics-Informed Neural Networks (FBPINNs) and their multilevel extensions as a promising alternative. These methods leverage domain decomposition, partitioning the computational domain into overlapping sub-domains, each governed by a local neural network. We assess their accuracy and computational efficiency in solving the Helmholtz equation for the homogeneous case, demonstrating their potential to mitigate the limitations of traditional approaches.

Generalizing the SINDy approach with nested neural networks

Symbolic Regression (SR) is a widely studied field of research that aims to infer symbolic expressions from data. A popular approach for SR is the Sparse Identification of Nonlinear Dynamical Systems (\sindy) framework, which uses sparse regression to identify governing equations from data. This study introduces an enhanced method, Nested SINDy, that aims to increase the expressivity of the SINDy approach thanks to a nested structure. Indeed, traditional symbolic regression and system identification methods often fail with complex systems that cannot be easily described analytically. Nested SINDy builds on the SINDy framework by introducing additional layers before and after the core SINDy layer. This allows the method to identify symbolic representations for a wider range of systems, including those with compositions and products of functions. We demonstrate the ability of the Nested SINDy approach to accurately find symbolic expressions for simple systems, such as basic trigonometric functions, and sparse (false but accurate) analytical representations for more complex systems. Our results highlight Nested SINDy's potential as a tool for symbolic regression, surpassing the traditional SINDy approach in terms of expressivity. However, we also note the challenges in the optimization process for Nested SINDy and suggest future research directions, including the designing of a more robust methodology for the optimization process. This study proves that Nested SINDy can effectively discover symbolic representations of dynamical systems from data, offering new opportunities for understanding complex systems through data-driven methods.