Towards quantum advantage for topological data analysis

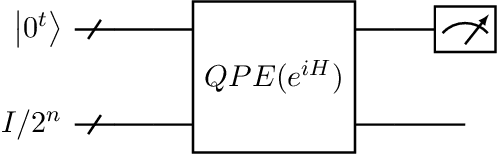
A particularly promising line of quantum machine leaning (QML) algorithms with the potential to exhibit exponential speedups over their classical counterparts has recently been set back by a series of "dequantization" results, that is, quantum-inspired classical algorithms which perform equally well in essence. This raises the important question whether other QML algorithms are susceptible to such dequantization, or whether it can be formally argued that they are out of reach of classical computers. In this paper, we study the quantum algorithm for topological data analysis by Lloyd, Garnerone and Zanardi (LGZ). We provide evidence that certain crucial steps in this algorithm solve problems that are classically intractable by closely relating them to the one clean qubit model, a restricted model of quantum computation whose power is strongly believed to lie beyond that of classical computation. While our results do not imply that the topological data analysis problem solved by the LGZ algorithm (i.e., Betti number estimation) is itself DQC1-hard, our work does provide the first steps towards answering the question of whether it is out of reach of classical computers. Additionally, we discuss how to extend the applicability of this algorithm beyond its original aim of estimating Betti numbers and demonstrate this by looking into quantum algorithms for spectral entropy estimation. Finally, we briefly consider the suitability of the LGZ algorithm for near-term implementations.

A framework for deep energy-based reinforcement learning with quantum speed-up

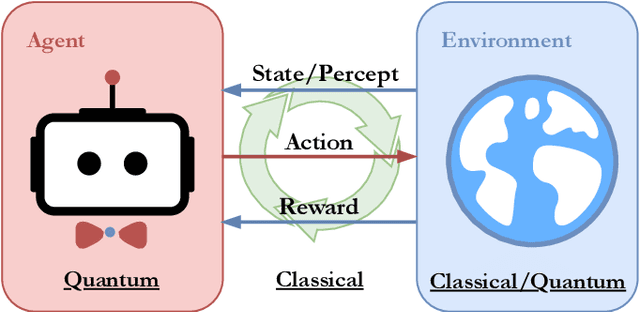
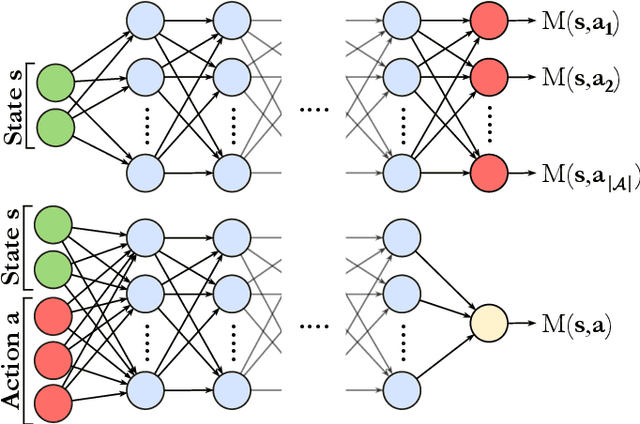
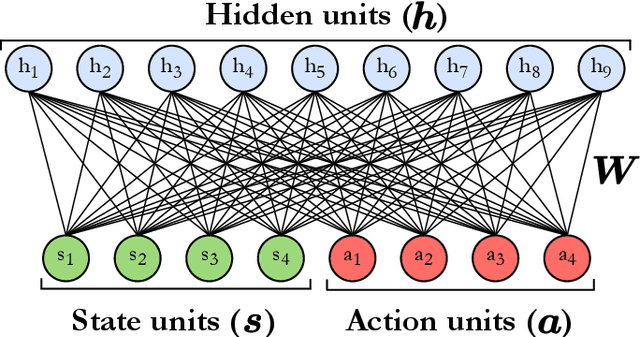
In the past decade, deep learning methods have seen tremendous success in various supervised and unsupervised learning tasks such as classification and generative modeling. More recently, deep neural networks have emerged in the domain of reinforcement learning as a tool to solve decision-making problems of unprecedented complexity, e.g., navigation problems or game-playing AI. Despite the successful combinations of ideas from quantum computing with machine learning methods, there have been relatively few attempts to design quantum algorithms that would enhance deep reinforcement learning. This is partly due to the fact that quantum enhancements of deep neural networks, in general, have not been as extensively investigated as other quantum machine learning methods. In contrast, projective simulation is a reinforcement learning model inspired by the stochastic evolution of physical systems that enables a quantum speed-up in decision making. In this paper, we develop a unifying framework that connects deep learning and projective simulation, opening the route to quantum improvements in deep reinforcement learning. Our approach is based on so-called generative energy-based models to design reinforcement learning methods with a computational advantage in solving complex and large-scale decision-making problems.

On the convergence of projective-simulation-based reinforcement learning in Markov decision processes

In recent years, the interest in leveraging quantum effects for enhancing machine learning tasks has significantly increased. Many algorithms speeding up supervised and unsupervised learning were established. The first framework in which ways to exploit quantum resources specifically for the broader context of reinforcement learning were found is projective simulation. Projective simulation presents an agent-based reinforcement learning approach designed in a manner which may support quantum walk-based speed-ups. Although classical variants of projective simulation have been benchmarked against common reinforcement learning algorithms, very few formal theoretical analyses have been provided for its performance in standard learning scenarios. In this paper, we provide a detailed formal discussion of the properties of this model. Specifically, we prove that one version of the projective simulation model, understood as a reinforcement learning approach, converges to optimal behavior in a large class of Markov decision processes. This proof shows that a physically-inspired approach to reinforcement learning can guarantee to converge.

Optimizing Quantum Error Correction Codes with Reinforcement Learning

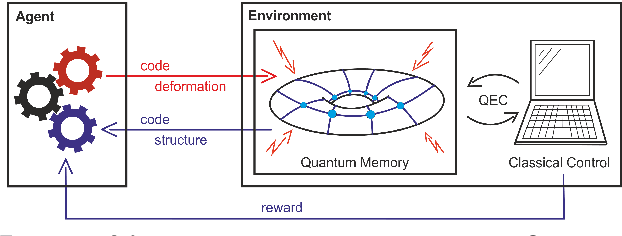
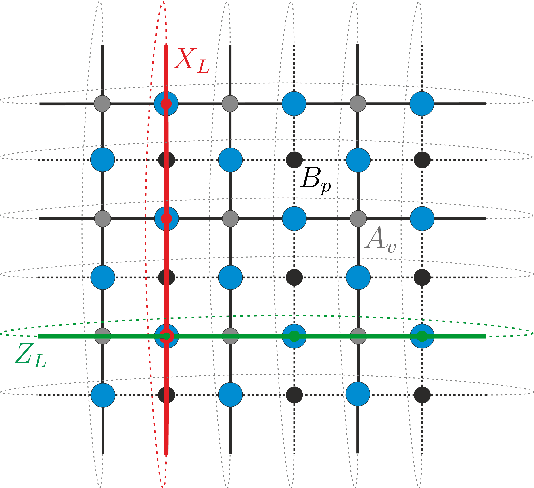
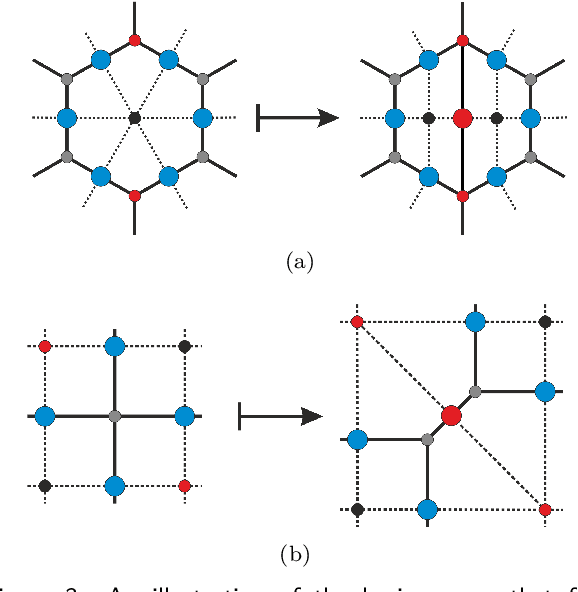
Quantum error correction is widely thought to be the key to fault-tolerant quantum computation. However, determining the most suited encoding for unknown error channels or specific laboratory setups is highly challenging. Here, we present a reinforcement learning framework for optimizing and fault-tolerantly adapting quantum error correction codes. We consider a reinforcement learning agent tasked with modifying a quantum memory until a desired logical error rate is reached. Using efficient simulations of a surface code quantum memory with about 70 physical qubits, we demonstrate that such a reinforcement learning agent can determine near-optimal solutions, in terms of the number of physical qubits, for various error models of interest. Moreover, we show that agents trained on one task are able to transfer their experience to similar tasks. This ability for transfer learning showcases the inherent strengths of reinforcement learning and the applicability of our approach for optimization both in off-line simulations and on-line under laboratory conditions.

Faster quantum mixing for slowly evolving sequences of Markov chains

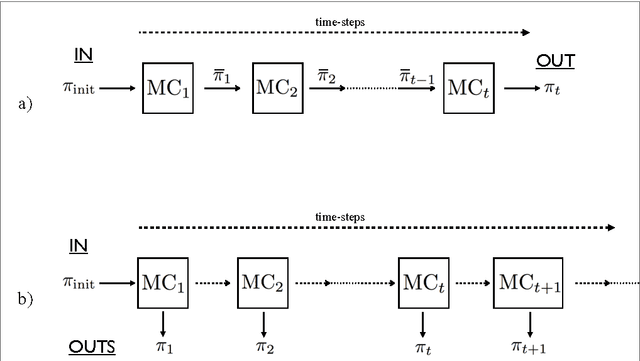
Markov chain methods are remarkably successful in computational physics, machine learning, and combinatorial optimization. The cost of such methods often reduces to the mixing time, i.e., the time required to reach the steady state of the Markov chain, which scales as $\delta^{-1}$, the inverse of the spectral gap. It has long been conjectured that quantum computers offer nearly generic quadratic improvements for mixing problems. However, except in special cases, quantum algorithms achieve a run-time of $\mathcal{O}(\sqrt{\delta^{-1}} \sqrt{N})$, which introduces a costly dependence on the Markov chain size $N,$ not present in the classical case. Here, we re-address the problem of mixing of Markov chains when these form a slowly evolving sequence. This setting is akin to the simulated annealing setting and is commonly encountered in physics, material sciences and machine learning. We provide a quantum memory-efficient algorithm with a run-time of $\mathcal{O}(\sqrt{\delta^{-1}} \sqrt[4]{N})$, neglecting logarithmic terms, which is an important improvement for large state spaces. Moreover, our algorithms output quantum encodings of distributions, which has advantages over classical outputs. Finally, we discuss the run-time bounds of mixing algorithms and show that, under certain assumptions, our algorithms are optimal.

Exponential improvements for quantum-accessible reinforcement learning

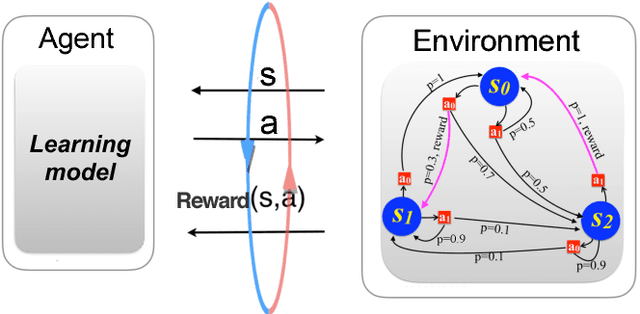
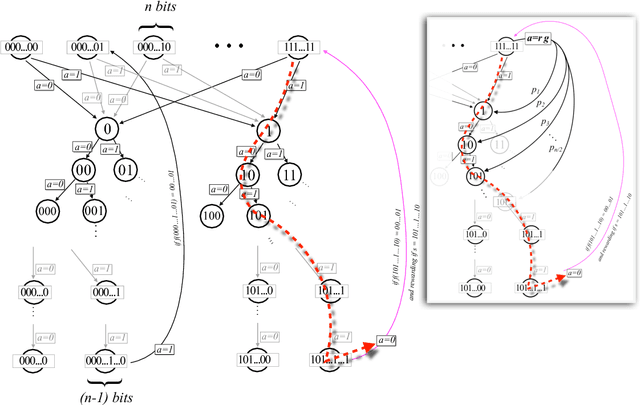
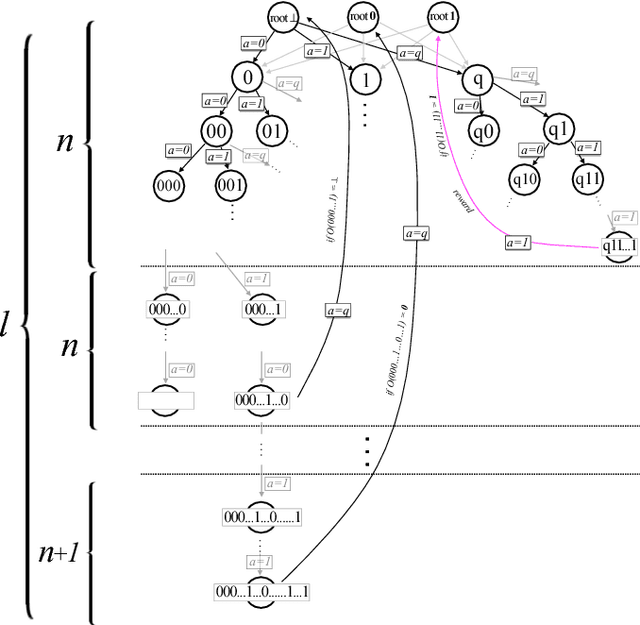
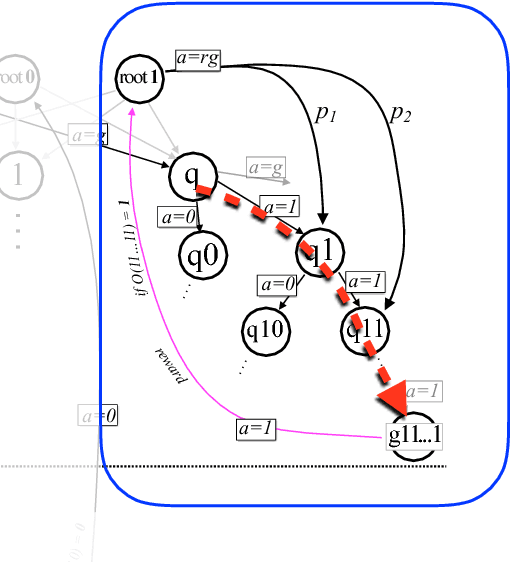
Quantum computers can offer dramatic improvements over classical devices for data analysis tasks such as prediction and classification. However, less is known about the advantages that quantum computers may bring in the setting of reinforcement learning, where learning is achieved via interaction with a task environment. Here, we consider a special case of reinforcement learning, where the task environment allows quantum access. In addition, we impose certain "naturalness" conditions on the task environment, which rule out the kinds of oracle problems that are studied in quantum query complexity (and for which quantum speedups are well-known). Within this framework of quantum-accessible reinforcement learning environments, we demonstrate that quantum agents can achieve exponential improvements in learning efficiency, surpassing previous results that showed only quadratic improvements. A key step in the proof is to construct task environments that encode well-known oracle problems, such as Simon's problem and Recursive Fourier Sampling, while satisfying the above "naturalness" conditions for reinforcement learning. Our results suggest that quantum agents may perform well in certain game-playing scenarios, where the game has recursive structure, and the agent can learn by playing against itself.

Computational speedups using small quantum devices

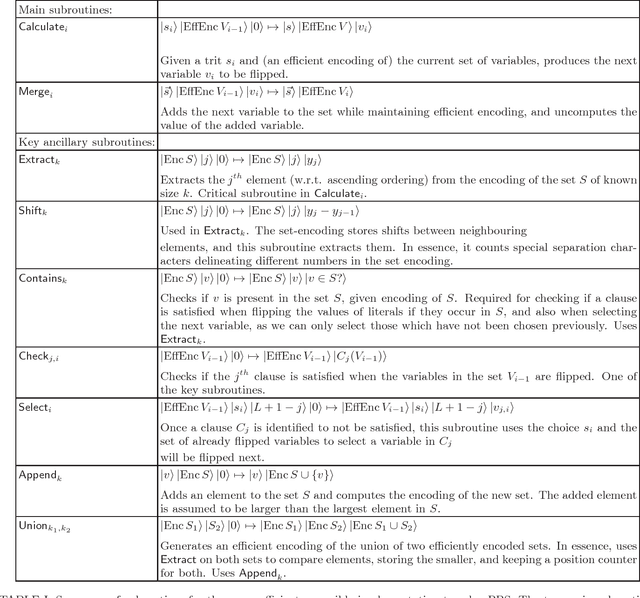
Suppose we have a small quantum computer with only M qubits. Can such a device genuinely speed up certain algorithms, even when the problem size is much larger than M? Here we answer this question to the affirmative. We present a hybrid quantum-classical algorithm to solve 3SAT problems involving n>>M variables that significantly speeds up its fully classical counterpart. This question may be relevant in view of the current quest to build small quantum computers.

A note on state preparation for quantum machine learning

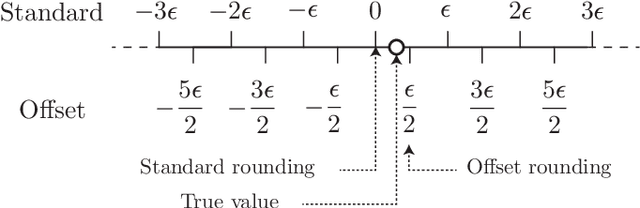
The intersection between the fields of machine learning and quantum information processing is proving to be a fruitful field for the discovery of new quantum algorithms, which potentially offer an exponential speed-up over their classical counterparts. However, many such algorithms require the ability to produce states proportional to vectors stored in quantum memory. Even given access to quantum databases which store exponentially long vectors, the construction of which is considered a one-off overhead, it has been argued that the cost of preparing such amplitude-encoded states may offset any exponential quantum advantage. Here we argue that specifically in the context of machine learning applications it suffices to prepare a state close to the ideal state only in the $\infty$-norm, and that this can be achieved with only a constant number of memory queries.

Active learning machine learns to create new quantum experiments

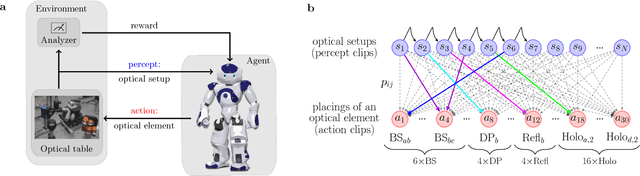
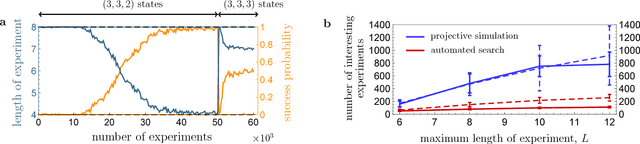
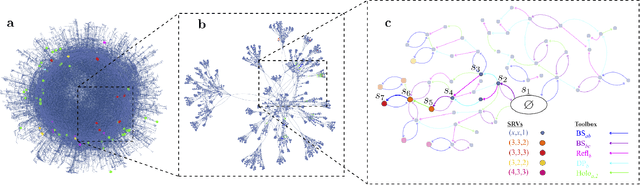
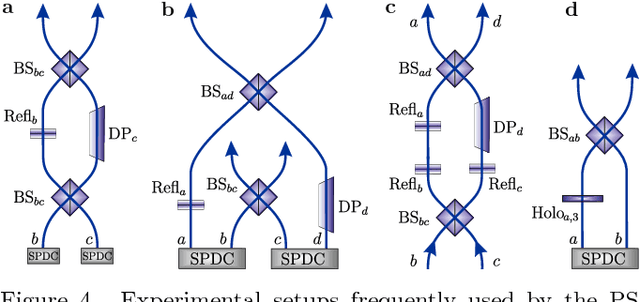
How useful can machine learning be in a quantum laboratory? Here we raise the question of the potential of intelligent machines in the context of scientific research. A major motivation for the present work is the unknown reachability of various entanglement classes in quantum experiments. We investigate this question by using the projective simulation model, a physics-oriented approach to artificial intelligence. In our approach, the projective simulation system is challenged to design complex photonic quantum experiments that produce high-dimensional entangled multiphoton states, which are of high interest in modern quantum experiments. The artificial intelligence system learns to create a variety of entangled states, and improves the efficiency of their realization. In the process, the system autonomously (re)discovers experimental techniques which are only now becoming standard in modern quantum optical experiments - a trait which was not explicitly demanded from the system but emerged through the process of learning. Such features highlight the possibility that machines could have a significantly more creative role in future research.

Projective simulation with generalization

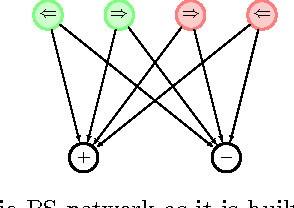
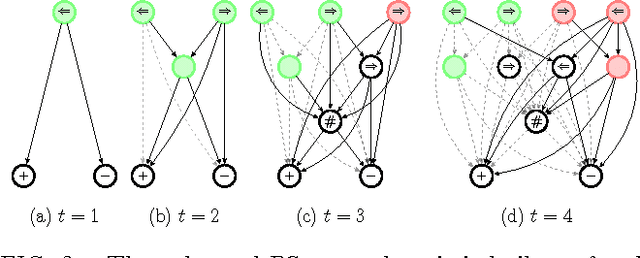
The ability to generalize is an important feature of any intelligent agent. Not only because it may allow the agent to cope with large amounts of data, but also because in some environments, an agent with no generalization capabilities cannot learn. In this work we outline several criteria for generalization, and present a dynamic and autonomous machinery that enables projective simulation agents to meaningfully generalize. Projective simulation, a novel, physical approach to artificial intelligence, was recently shown to perform well in standard reinforcement learning problems, with applications in advanced robotics as well as quantum experiments. Both the basic projective simulation model and the presented generalization machinery are based on very simple principles. This allows us to provide a full analytical analysis of the agent's performance and to illustrate the benefit the agent gains by generalizing. Specifically, we show that already in basic (but extreme) environments, learning without generalization may be impossible, and demonstrate how the presented generalization machinery enables the projective simulation agent to learn.