A Scalable Gradient-Based Optimization Framework for Sparse Minimum-Variance Portfolio Selection

Portfolio optimization involves selecting asset weights to minimize a risk-reward objective, such as the portfolio variance in the classical minimum-variance framework. Sparse portfolio selection extends this by imposing a cardinality constraint: only $k$ assets from a universe of $p$ may be included. The standard approach models this problem as a mixed-integer quadratic program and relies on commercial solvers to find the optimal solution. However, the computational costs of such methods increase exponentially with $k$ and $p$, making them too slow for problems of even moderate size. We propose a fast and scalable gradient-based approach that transforms the combinatorial sparse selection problem into a constrained continuous optimization task via Boolean relaxation, while preserving equivalence with the original problem on the set of binary points. Our algorithm employs a tunable parameter that transmutes the auxiliary objective from a convex to a concave function. This allows a stable convex starting point, followed by a controlled path toward a sparse binary solution as the tuning parameter increases and the objective moves toward concavity. In practice, our method matches commercial solvers in asset selection for most instances and, in rare instances, the solution differs by a few assets whilst showing a negligible error in portfolio variance.

Robust Classification via Support Vector Machines

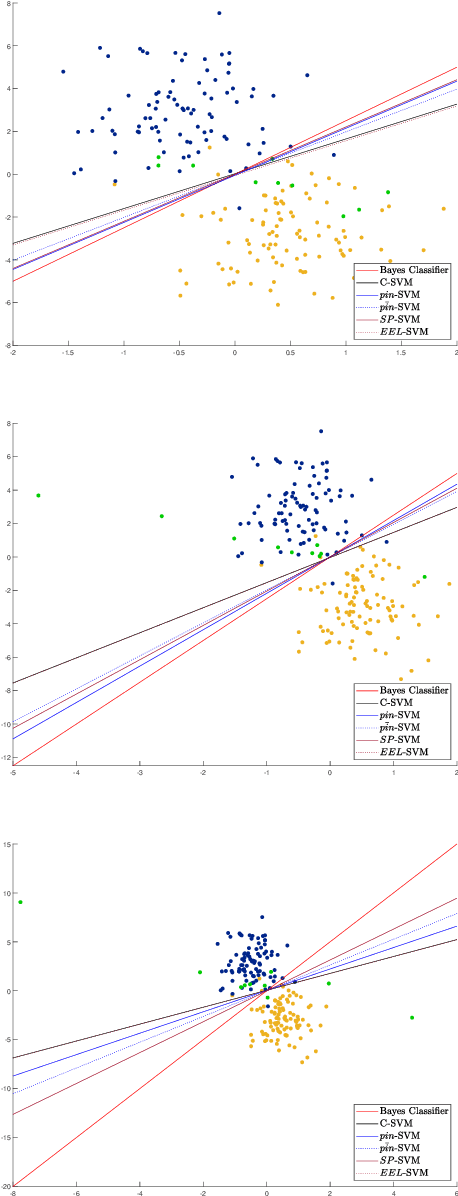
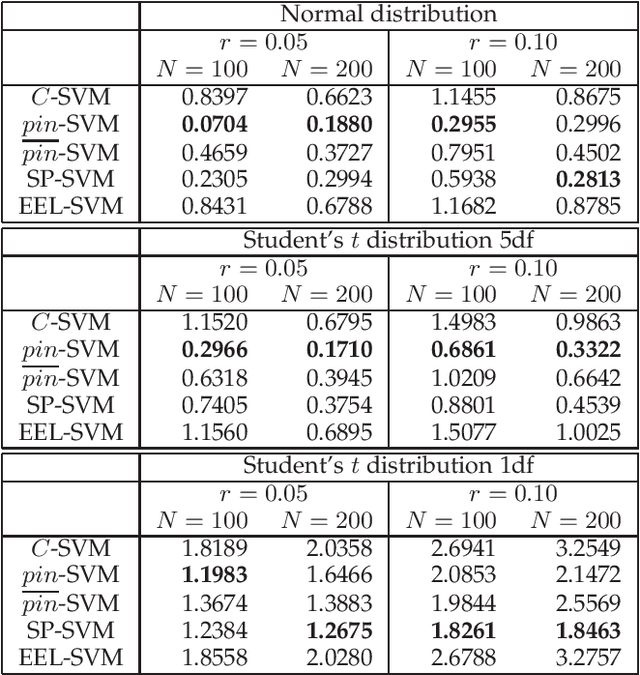
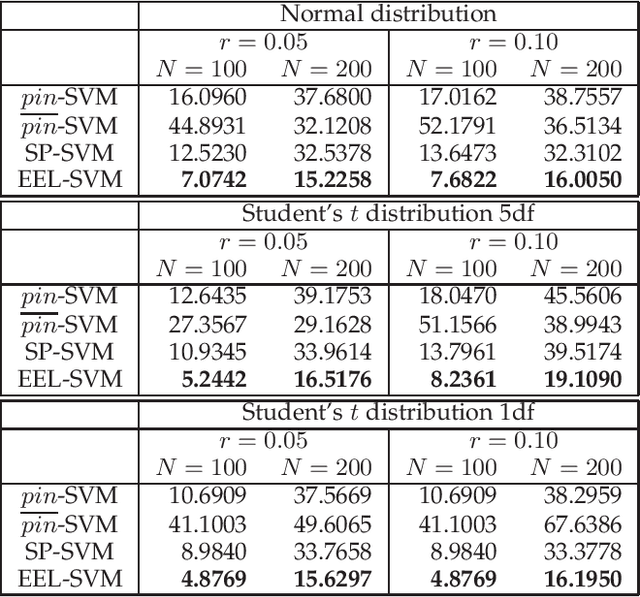
The loss function choice for any Support Vector Machine classifier has raised great interest in the literature due to the lack of robustness of the Hinge loss, which is the standard loss choice. In this paper, we plan to robustify the binary classifier by maintaining the overall advantages of the Hinge loss, rather than modifying this standard choice. We propose two robust classifiers under data uncertainty. The first is called Single Perturbation SVM (SP-SVM) and provides a constructive method by allowing a controlled perturbation to one feature of the data. The second method is called Extreme Empirical Loss SVM (EEL-SVM) and is based on a new empirical loss estimate, namely, the Extreme Empirical Loss (EEL), that puts more emphasis on extreme violations of the classification hyper-plane, rather than taking the usual sample average with equal importance for all hyper-plane violations. Extensive numerical investigation reveals the advantages of the two robust classifiers on simulated data and well-known real datasets.