A Scalable Gradient-Based Optimization Framework for Sparse Minimum-Variance Portfolio Selection

Portfolio optimization involves selecting asset weights to minimize a risk-reward objective, such as the portfolio variance in the classical minimum-variance framework. Sparse portfolio selection extends this by imposing a cardinality constraint: only $k$ assets from a universe of $p$ may be included. The standard approach models this problem as a mixed-integer quadratic program and relies on commercial solvers to find the optimal solution. However, the computational costs of such methods increase exponentially with $k$ and $p$, making them too slow for problems of even moderate size. We propose a fast and scalable gradient-based approach that transforms the combinatorial sparse selection problem into a constrained continuous optimization task via Boolean relaxation, while preserving equivalence with the original problem on the set of binary points. Our algorithm employs a tunable parameter that transmutes the auxiliary objective from a convex to a concave function. This allows a stable convex starting point, followed by a controlled path toward a sparse binary solution as the tuning parameter increases and the objective moves toward concavity. In practice, our method matches commercial solvers in asset selection for most instances and, in rare instances, the solution differs by a few assets whilst showing a negligible error in portfolio variance.

Continuous Optimization for Offline Change Point Detection and Estimation

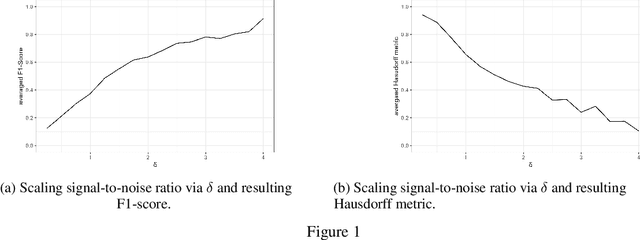
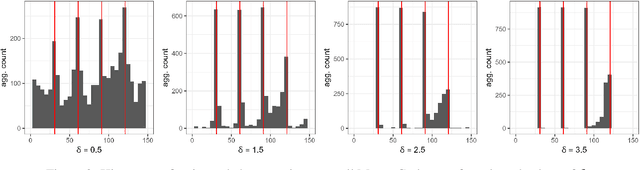
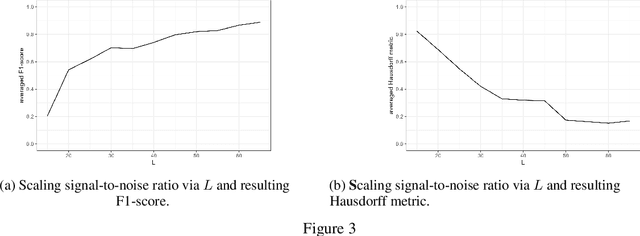
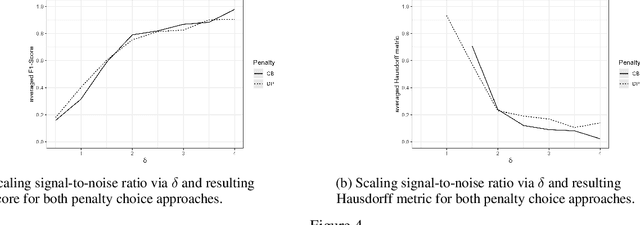
This work explores use of novel advances in best subset selection for regression modelling via continuous optimization for offline change point detection and estimation in univariate Gaussian data sequences. The approach exploits reformulating the normal mean multiple change point model into a regularized statistical inverse problem enforcing sparsity. After introducing the problem statement, criteria and previous investigations via Lasso-regularization, the recently developed framework of continuous optimization for best subset selection (COMBSS) is briefly introduced and related to the problem at hand. Supervised and unsupervised perspectives are explored with the latter testing different approaches for the choice of regularization penalty parameters via the discrepancy principle and a confidence bound. The main result is an adaptation and evaluation of the COMBSS approach for offline normal mean multiple change-point detection via experimental results on simulated data for different choices of regularisation parameters. Results and future directions are discussed.

Variance Reduction for Matrix Computations with Applications to Gaussian Processes

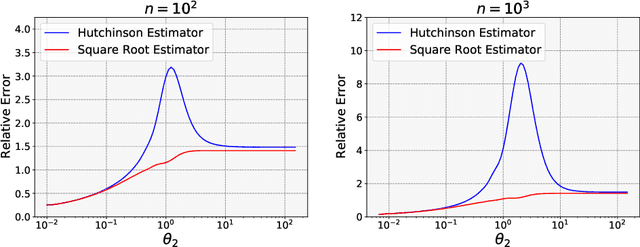
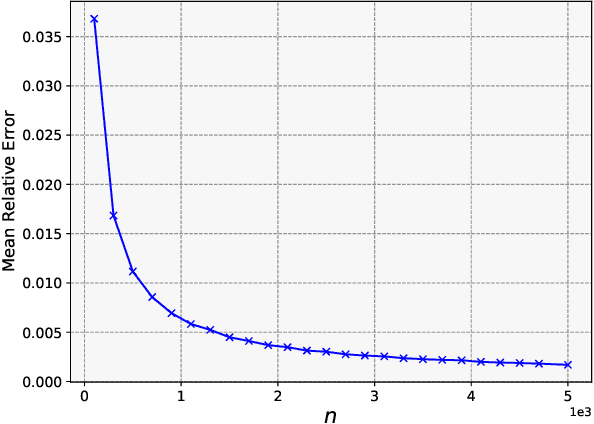
In addition to recent developments in computing speed and memory, methodological advances have contributed to significant gains in the performance of stochastic simulation. In this paper, we focus on variance reduction for matrix computations via matrix factorization. We provide insights into existing variance reduction methods for estimating the entries of large matrices. Popular methods do not exploit the reduction in variance that is possible when the matrix is factorized. We show how computing the square root factorization of the matrix can achieve in some important cases arbitrarily better stochastic performance. In addition, we propose a factorized estimator for the trace of a product of matrices and numerically demonstrate that the estimator can be up to 1,000 times more efficient on certain problems of estimating the log-likelihood of a Gaussian process. Additionally, we provide a new estimator of the log-determinant of a positive semi-definite matrix where the log-determinant is treated as a normalizing constant of a probability density.