Differentiable Interacting Multiple Model Particle Filtering

We propose a sequential Monte Carlo algorithm for parameter learning when the studied model exhibits random discontinuous jumps in behaviour. To facilitate the learning of high dimensional parameter sets, such as those associated to neural networks, we adopt the emerging framework of differentiable particle filtering, wherein parameters are trained by gradient descent. We design a new differentiable interacting multiple model particle filter to be capable of learning the individual behavioural regimes and the model which controls the jumping simultaneously. In contrast to previous approaches, our algorithm allows control of the computational effort assigned per regime whilst using the probability of being in a given regime to guide sampling. Furthermore, we develop a new gradient estimator that has a lower variance than established approaches and remains fast to compute, for which we prove consistency. We establish new theoretical results of the presented algorithms and demonstrate superior numerical performance compared to the previous state-of-the-art algorithms.

Efficient Mixture Learning in Black-Box Variational Inference

Mixture variational distributions in black box variational inference (BBVI) have demonstrated impressive results in challenging density estimation tasks. However, currently scaling the number of mixture components can lead to a linear increase in the number of learnable parameters and a quadratic increase in inference time due to the evaluation of the evidence lower bound (ELBO). Our two key contributions address these limitations. First, we introduce the novel Multiple Importance Sampling Variational Autoencoder (MISVAE), which amortizes the mapping from input to mixture-parameter space using one-hot encodings. Fortunately, with MISVAE, each additional mixture component incurs a negligible increase in network parameters. Second, we construct two new estimators of the ELBO for mixtures in BBVI, enabling a tremendous reduction in inference time with marginal or even improved impact on performance. Collectively, our contributions enable scalability to hundreds of mixture components and provide superior estimation performance in shorter time, with fewer network parameters compared to previous Mixture VAEs. Experimenting with MISVAE, we achieve astonishing, SOTA results on MNIST. Furthermore, we empirically validate our estimators in other BBVI settings, including Bayesian phylogenetic inference, where we improve inference times for the SOTA mixture model on eight data sets.

Adaptive importance sampling for heavy-tailed distributions via $α$-divergence minimization

Adaptive importance sampling (AIS) algorithms are widely used to approximate expectations with respect to complicated target probability distributions. When the target has heavy tails, existing AIS algorithms can provide inconsistent estimators or exhibit slow convergence, as they often neglect the target's tail behaviour. To avoid this pitfall, we propose an AIS algorithm that approximates the target by Student-t proposal distributions. We adapt location and scale parameters by matching the escort moments - which are defined even for heavy-tailed distributions - of the target and the proposal. These updates minimize the $\alpha$-divergence between the target and the proposal, thereby connecting with variational inference. We then show that the $\alpha$-divergence can be approximated by a generalized notion of effective sample size and leverage this new perspective to adapt the tail parameter with Bayesian optimization. We demonstrate the efficacy of our approach through applications to synthetic targets and a Bayesian Student-t regression task on a real example with clinical trial data.

Graphs in State-Space Models for Granger Causality in Climate Science

Granger causality (GC) is often considered not an actual form of causality. Still, it is arguably the most widely used method to assess the predictability of a time series from another one. Granger causality has been widely used in many applied disciplines, from neuroscience and econometrics to Earth sciences. We revisit GC under a graphical perspective of state-space models. For that, we use GraphEM, a recently presented expectation-maximisation algorithm for estimating the linear matrix operator in the state equation of a linear-Gaussian state-space model. Lasso regularisation is included in the M-step, which is solved using a proximal splitting Douglas-Rachford algorithm. Experiments in toy examples and challenging climate problems illustrate the benefits of the proposed model and inference technique over standard Granger causality methods.

Differentiable Bootstrap Particle Filters for Regime-Switching Models

Differentiable particle filters are an emerging class of particle filtering methods that use neural networks to construct and learn parametric state-space models. In real-world applications, both the state dynamics and measurements can switch between a set of candidate models. For instance, in target tracking, vehicles can idle, move through traffic, or cruise on motorways, and measurements are collected in different geographical or weather conditions. This paper proposes a new differentiable particle filter for regime-switching state-space models. The method can learn a set of unknown candidate dynamic and measurement models and track the state posteriors. We evaluate the performance of the novel algorithm in relevant models, showing its great performance compared to other competitive algorithms.

Learning with MISELBO: The Mixture Cookbook

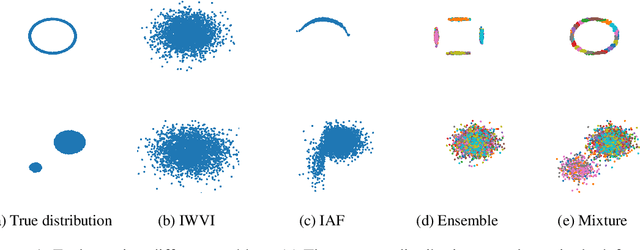
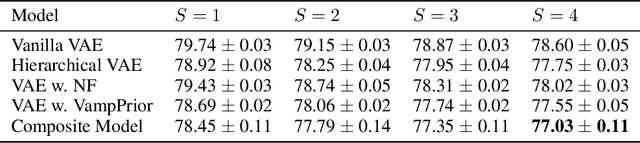
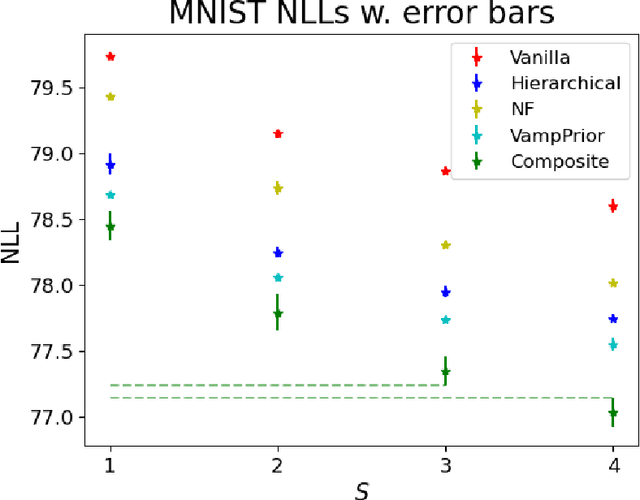
Mixture models in variational inference (VI) is an active field of research. Recent works have established their connection to multiple importance sampling (MIS) through the MISELBO and advanced the use of ensemble approximations for large-scale problems. However, as we show here, an independent learning of the ensemble components can lead to suboptimal diversity. Hence, we study the effect of instead using MISELBO as an objective function for learning mixtures, and we propose the first ever mixture of variational approximations for a normalizing flow-based hierarchical variational autoencoder (VAE) with VampPrior and a PixelCNN decoder network. Two major insights led to the construction of this novel composite model. First, mixture models have potential to be off-the-shelf tools for practitioners to obtain more flexible posterior approximations in VAEs. Therefore, we make them more accessible by demonstrating how to apply them to four popular architectures. Second, the mixture components cooperate in order to cover the target distribution while trying to maximize their diversity when MISELBO is the objective function. We explain this cooperative behavior by drawing a novel connection between VI and adaptive importance sampling. Finally, we demonstrate the superiority of the Mixture VAEs' learned feature representations on both image and single-cell transcriptome data, and obtain state-of-the-art results among VAE architectures in terms of negative log-likelihood on the MNIST and FashionMNIST datasets. Code available here: \url{https://github.com/Lagergren-Lab/MixtureVAEs}.

Hamiltonian Adaptive Importance Sampling

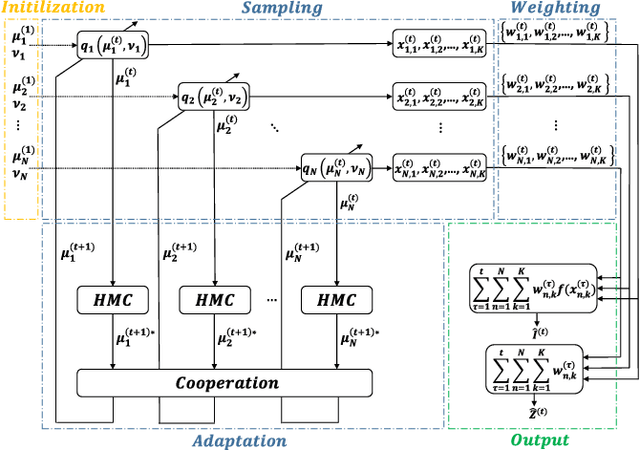
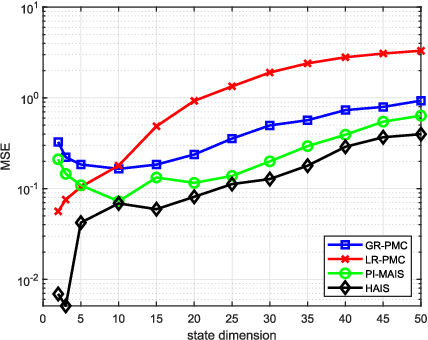
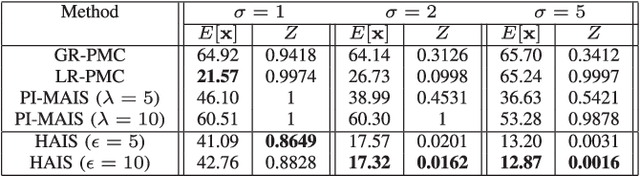
Importance sampling (IS) is a powerful Monte Carlo (MC) methodology for approximating integrals, for instance in the context of Bayesian inference. In IS, the samples are simulated from the so-called proposal distribution, and the choice of this proposal is key for achieving a high performance. In adaptive IS (AIS) methods, a set of proposals is iteratively improved. AIS is a relevant and timely methodology although many limitations remain yet to be overcome, e.g., the curse of dimensionality in high-dimensional and multi-modal problems. Moreover, the Hamiltonian Monte Carlo (HMC) algorithm has become increasingly popular in machine learning and statistics. HMC has several appealing features such as its exploratory behavior, especially in high-dimensional targets, when other methods suffer. In this paper, we introduce the novel Hamiltonian adaptive importance sampling (HAIS) method. HAIS implements a two-step adaptive process with parallel HMC chains that cooperate at each iteration. The proposed HAIS efficiently adapts a population of proposals, extracting the advantages of HMC. HAIS can be understood as a particular instance of the generic layered AIS family with an additional resampling step. HAIS achieves a significant performance improvement in high-dimensional problems w.r.t. state-of-the-art algorithms. We discuss the statistical properties of HAIS and show its high performance in two challenging examples.

Multiple Importance Sampling ELBO and Deep Ensembles of Variational Approximations

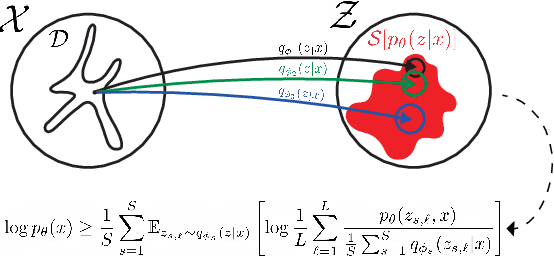
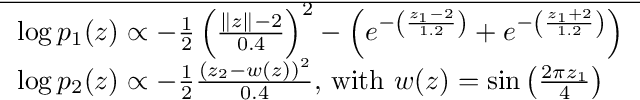
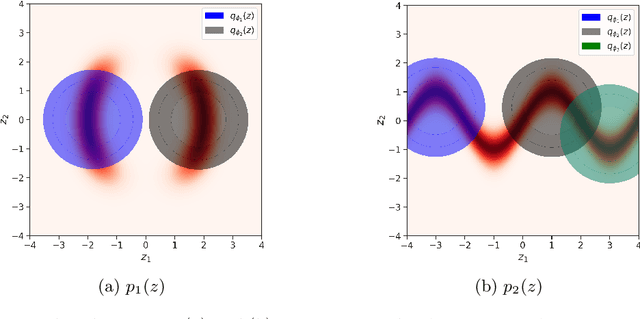
In variational inference (VI), the marginal log-likelihood is estimated using the standard evidence lower bound (ELBO), or improved versions as the importance weighted ELBO (IWELBO). We propose the multiple importance sampling ELBO (MISELBO), a \textit{versatile} yet \textit{simple} framework. MISELBO is applicable in both amortized and classical VI, and it uses ensembles, e.g., deep ensembles, of independently inferred variational approximations. As far as we are aware, the concept of deep ensembles in amortized VI has not previously been established. We prove that MISELBO provides a tighter bound than the average of standard ELBOs, and demonstrate empirically that it gives tighter bounds than the average of IWELBOs. MISELBO is evaluated in density-estimation experiments that include MNIST and several real-data phylogenetic tree inference problems. First, on the MNIST dataset, MISELBO boosts the density-estimation performances of a state-of-the-art model, nouveau VAE. Second, in the phylogenetic tree inference setting, our framework enhances a state-of-the-art VI algorithm that uses normalizing flows. On top of the technical benefits of MISELBO, it allows to unveil connections between VI and recent advances in the importance sampling literature, paving the way for further methodological advances. We provide our code at \url{https://github.com/Lagergren-Lab/MISELBO}.

Compressed particle methods for expensive models with application in Astronomy and Remote Sensing

In many inference problems, the evaluation of complex and costly models is often required. In this context, Bayesian methods have become very popular in several fields over the last years, in order to obtain parameter inversion, model selection or uncertainty quantification. Bayesian inference requires the approximation of complicated integrals involving (often costly) posterior distributions. Generally, this approximation is obtained by means of Monte Carlo (MC) methods. In order to reduce the computational cost of the corresponding technique, surrogate models (also called emulators) are often employed. Another alternative approach is the so-called Approximate Bayesian Computation (ABC) scheme. ABC does not require the evaluation of the costly model but the ability to simulate artificial data according to that model. Moreover, in ABC, the choice of a suitable distance between real and artificial data is also required. In this work, we introduce a novel approach where the expensive model is evaluated only in some well-chosen samples. The selection of these nodes is based on the so-called compressed Monte Carlo (CMC) scheme. We provide theoretical results supporting the novel algorithms and give empirical evidence of the performance of the proposed method in several numerical experiments. Two of them are real-world applications in astronomy and satellite remote sensing.

Compressed Monte Carlo with application in particle filtering

Bayesian models have become very popular over the last years in several fields such as signal processing, statistics, and machine learning. Bayesian inference requires the approximation of complicated integrals involving posterior distributions. For this purpose, Monte Carlo (MC) methods, such as Markov Chain Monte Carlo and importance sampling algorithms, are often employed. In this work, we introduce the theory and practice of a Compressed MC (C-MC) scheme to compress the statistical information contained in a set of random samples. In its basic version, C-MC is strictly related to the stratification technique, a well-known method used for variance reduction purposes. Deterministic C-MC schemes are also presented, which provide very good performance. The compression problem is strictly related to the moment matching approach applied in different filtering techniques, usually called as Gaussian quadrature rules or sigma-point methods. C-MC can be employed in a distributed Bayesian inference framework when cheap and fast communications with a central processor are required. Furthermore, C-MC is useful within particle filtering and adaptive IS algorithms, as shown by three novel schemes introduced in this work. Six numerical results confirm the benefits of the introduced schemes, outperforming the corresponding benchmark methods. A related code is also provided.