Harnessing physics-informed operators for high-dimensional reliability analysis problems

Reliability analysis is a formidable task, particularly in systems with a large number of stochastic parameters. Conventional methods for quantifying reliability often rely on extensive simulations or experimental data, which can be costly and time-consuming, especially when dealing with systems governed by complex physical laws which necessitates computationally intensive numerical methods such as finite element or finite volume techniques. On the other hand, surrogate-based methods offer an efficient alternative for computing reliability by approximating the underlying model from limited data. Neural operators have recently emerged as effective surrogates for modelling physical systems governed by partial differential equations. These operators can learn solutions to PDEs for varying inputs and parameters. Here, we investigate the efficacy of the recently developed physics-informed wavelet neural operator in solving reliability analysis problems. In particular, we investigate the possibility of using physics-informed operator for solving high-dimensional reliability analysis problems, while bypassing the need for any simulation. Through four numerical examples, we illustrate that physics-informed operator can seamlessly solve high-dimensional reliability analysis problems with reasonable accuracy, while eliminating the need for running expensive simulations.

DPA-WNO: A gray box model for a class of stochastic mechanics problem

The well-known governing physics in science and engineering is often based on certain assumptions and approximations. Therefore, analyses and designs carried out based on these equations are also approximate. The emergence of data-driven models has, to a certain degree, addressed this challenge; however, the purely data-driven models often (a) lack interpretability, (b) are data-hungry, and (c) do not generalize beyond the training window. Operator learning has recently been proposed as a potential alternative to address the aforementioned challenges; however, the challenges are still persistent. We here argue that one of the possible solutions resides in data-physics fusion, where the data-driven model is used to correct/identify the missing physics. To that end, we propose a novel Differentiable Physics Augmented Wavelet Neural Operator (DPA-WNO). The proposed DPA-WNO blends a differentiable physics solver with the Wavelet Neural Operator (WNO), where the role of WNO is to model the missing physics. This empowers the proposed framework to exploit the capability of WNO to learn from data while retaining the interpretability and generalizability associated with physics-based solvers. We illustrate the applicability of the proposed approach in solving time-dependent uncertainty quantification problems due to randomness in the initial condition. Four benchmark uncertainty quantification and reliability analysis examples from various fields of science and engineering are solved using the proposed approach. The results presented illustrate interesting features of the proposed approach.

Deep Physics Corrector: A physics enhanced deep learning architecture for solving stochastic differential equations

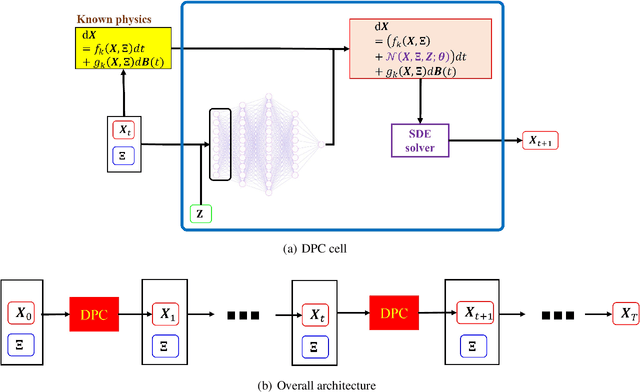
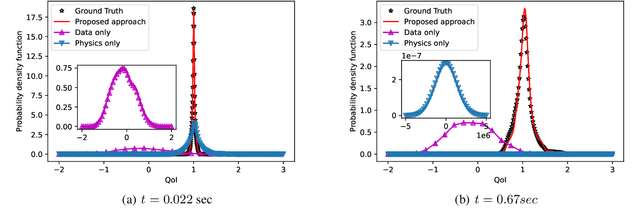
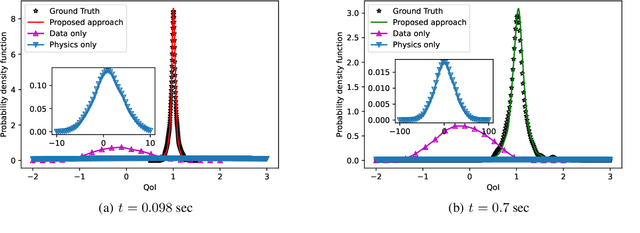
We propose a novel gray-box modeling algorithm for physical systems governed by stochastic differential equations (SDE). The proposed approach, referred to as the Deep Physics Corrector (DPC), blends approximate physics represented in terms of SDE with deep neural network (DNN). The primary idea here is to exploit DNN to model the missing physics. We hypothesize that combining incomplete physics with data will make the model interpretable and allow better generalization. The primary bottleneck associated with training surrogate models for stochastic simulators is often associated with selecting the suitable loss function. Among the different loss functions available in the literature, we use the conditional maximum mean discrepancy (CMMD) loss function in DPC because of its proven performance. Overall, physics-data fusion and CMMD allow DPC to learn from sparse data. We illustrate the performance of the proposed DPC on four benchmark examples from the literature. The results obtained are highly accurate, indicating its possible application as a surrogate model for stochastic simulators.

Persuasion Strategies in Advertisements: Dataset, Modeling, and Baselines

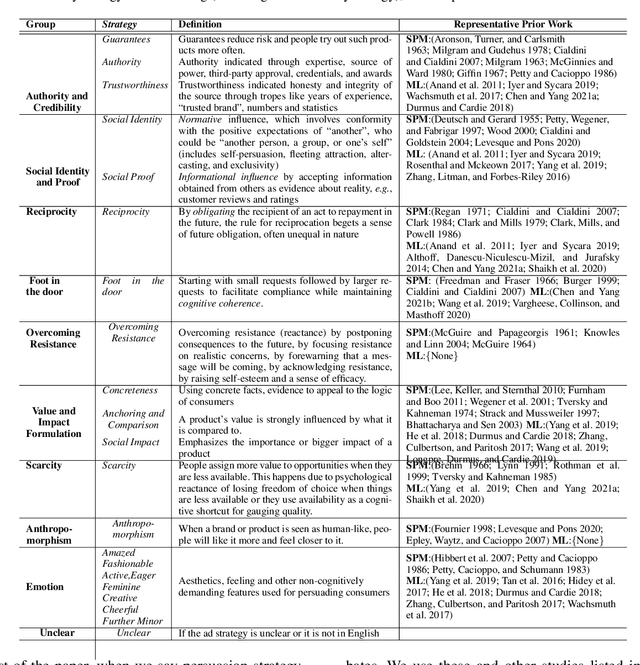
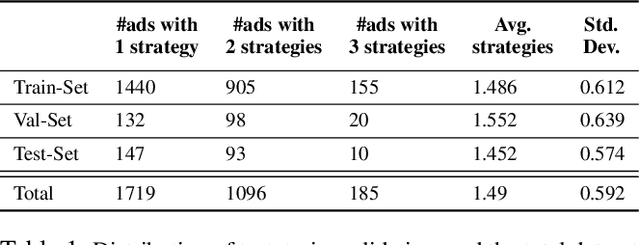
Modeling what makes an advertisement persuasive, i.e., eliciting the desired response from consumer, is critical to the study of propaganda, social psychology, and marketing. Despite its importance, computational modeling of persuasion in computer vision is still in its infancy, primarily due to the lack of benchmark datasets that can provide persuasion-strategy labels associated with ads. Motivated by persuasion literature in social psychology and marketing, we introduce an extensive vocabulary of persuasion strategies and build the first ad image corpus annotated with persuasion strategies. We then formulate the task of persuasion strategy prediction with multi-modal learning, where we design a multi-task attention fusion model that can leverage other ad-understanding tasks to predict persuasion strategies. Further, we conduct a real-world case study on 1600 advertising campaigns of 30 Fortune-500 companies where we use our model's predictions to analyze which strategies work with different demographics (age and gender). The dataset also provides image segmentation masks, which labels persuasion strategies in the corresponding ad images on the test split. We publicly release our code and dataset https://midas-research.github.io/persuasion-advertisements/.