Computational Performance Bounds Prediction in Quantum Computing with Unstable Noise

Quantum computing has significantly advanced in recent years, boasting devices with hundreds of quantum bits (qubits), hinting at its potential quantum advantage over classical computing. Yet, noise in quantum devices poses significant barriers to realizing this supremacy. Understanding noise's impact is crucial for reproducibility and application reuse; moreover, the next-generation quantum-centric supercomputing essentially requires efficient and accurate noise characterization to support system management (e.g., job scheduling), where ensuring correct functional performance (i.e., fidelity) of jobs on available quantum devices can even be higher-priority than traditional objectives. However, noise fluctuates over time, even on the same quantum device, which makes predicting the computational bounds for on-the-fly noise is vital. Noisy quantum simulation can offer insights but faces efficiency and scalability issues. In this work, we propose a data-driven workflow, namely QuBound, to predict computational performance bounds. It decomposes historical performance traces to isolate noise sources and devises a novel encoder to embed circuit and noise information processed by a Long Short-Term Memory (LSTM) network. For evaluation, we compare QuBound with a state-of-the-art learning-based predictor, which only generates a single performance value instead of a bound. Experimental results show that the result of the existing approach falls outside of performance bounds, while all predictions from our QuBound with the assistance of performance decomposition better fit the bounds. Moreover, QuBound can efficiently produce practical bounds for various circuits with over 106 speedup over simulation; in addition, the range from QuBound is over 10x narrower than the state-of-the-art analytical approach.

Adiabatic Quantum Support Vector Machines

Adiabatic quantum computers can solve difficult optimization problems (e.g., the quadratic unconstrained binary optimization problem), and they seem well suited to train machine learning models. In this paper, we describe an adiabatic quantum approach for training support vector machines. We show that the time complexity of our quantum approach is an order of magnitude better than the classical approach. Next, we compare the test accuracy of our quantum approach against a classical approach that uses the Scikit-learn library in Python across five benchmark datasets (Iris, Wisconsin Breast Cancer (WBC), Wine, Digits, and Lambeq). We show that our quantum approach obtains accuracies on par with the classical approach. Finally, we perform a scalability study in which we compute the total training times of the quantum approach and the classical approach with increasing number of features and number of data points in the training dataset. Our scalability results show that the quantum approach obtains a 3.5--4.5 times speedup over the classical approach on datasets with many (millions of) features.

Quantum Computing based Hybrid Solution Strategies for Large-scale Discrete-Continuous Optimization Problems

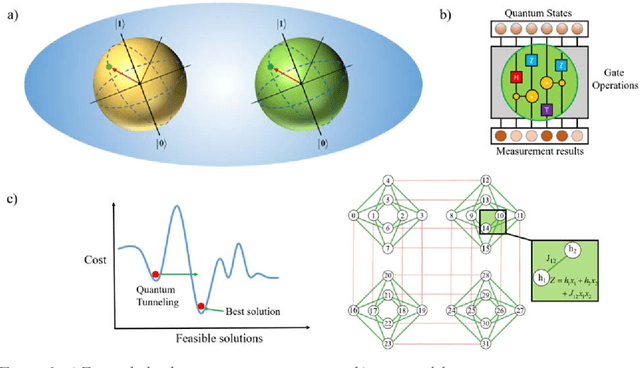
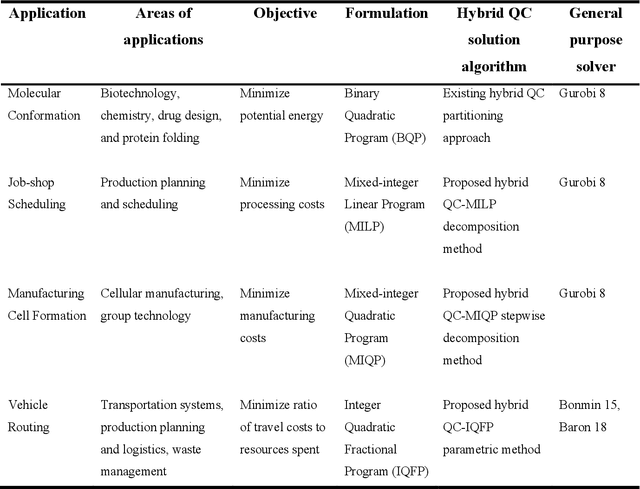
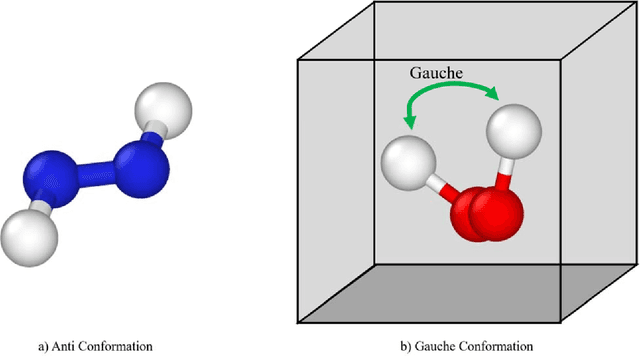
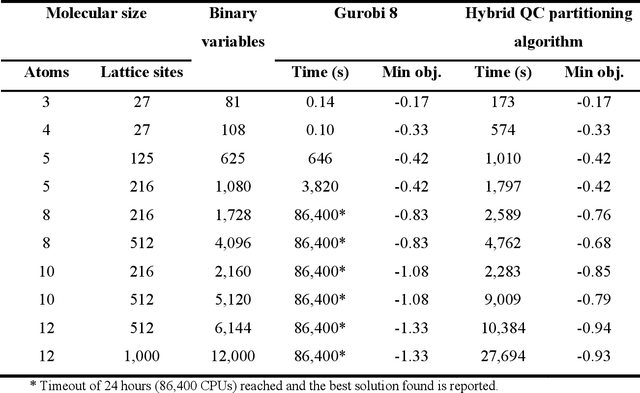
Quantum computing (QC) has gained popularity due to its unique capabilities that are quite different from that of classical computers in terms of speed and methods of operations. This paper proposes hybrid models and methods that effectively leverage the complementary strengths of deterministic algorithms and QC techniques to overcome combinatorial complexity for solving large-scale mixed-integer programming problems. Four applications, namely the molecular conformation problem, job-shop scheduling problem, manufacturing cell formation problem, and the vehicle routing problem, are specifically addressed. Large-scale instances of these application problems across multiple scales ranging from molecular design to logistics optimization are computationally challenging for deterministic optimization algorithms on classical computers. To address the computational challenges, hybrid QC-based algorithms are proposed and extensive computational experimental results are presented to demonstrate their applicability and efficiency. The proposed QC-based solution strategies enjoy high computational efficiency in terms of solution quality and computation time, by utilizing the unique features of both classical and quantum computers.