Bounded Regret for Finite-Armed Structured Bandits

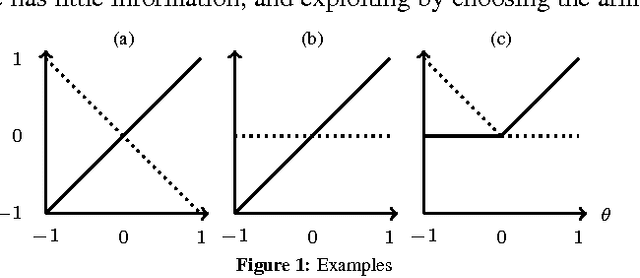
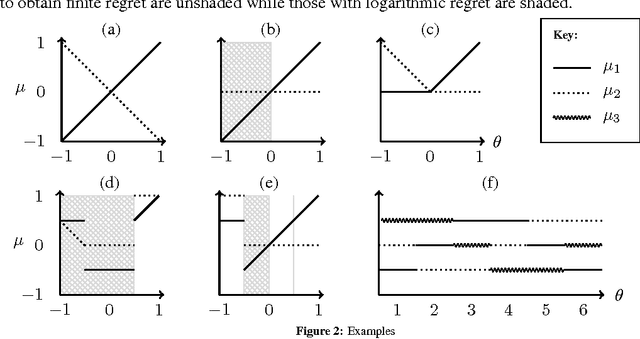
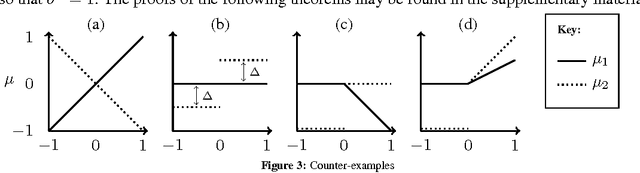
We study a new type of K-armed bandit problem where the expected return of one arm may depend on the returns of other arms. We present a new algorithm for this general class of problems and show that under certain circumstances it is possible to achieve finite expected cumulative regret. We also give problem-dependent lower bounds on the cumulative regret showing that at least in special cases the new algorithm is nearly optimal.

Optimal Resource Allocation with Semi-Bandit Feedback

We study a sequential resource allocation problem involving a fixed number of recurring jobs. At each time-step the manager should distribute available resources among the jobs in order to maximise the expected number of completed jobs. Allocating more resources to a given job increases the probability that it completes, but with a cut-off. Specifically, we assume a linear model where the probability increases linearly until it equals one, after which allocating additional resources is wasteful. We assume the difficulty of each job is unknown and present the first algorithm for this problem and prove upper and lower bounds on its regret. Despite its apparent simplicity, the problem has a rich structure: we show that an appropriate optimistic algorithm can improve its learning speed dramatically beyond the results one normally expects for similar problems as the problem becomes resource-laden.

The Sample-Complexity of General Reinforcement Learning

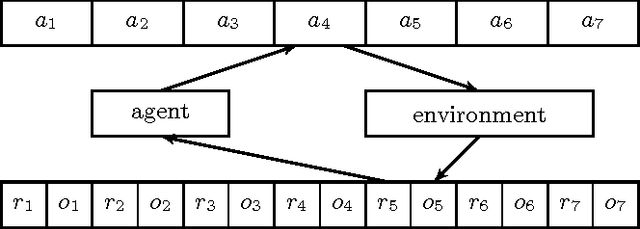
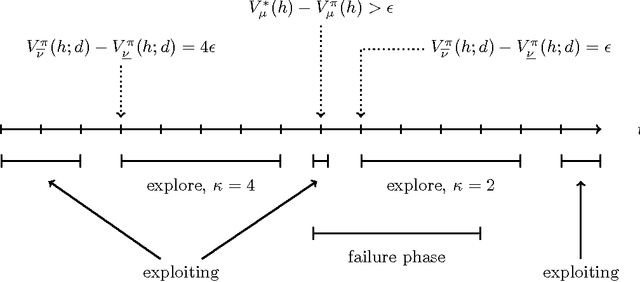
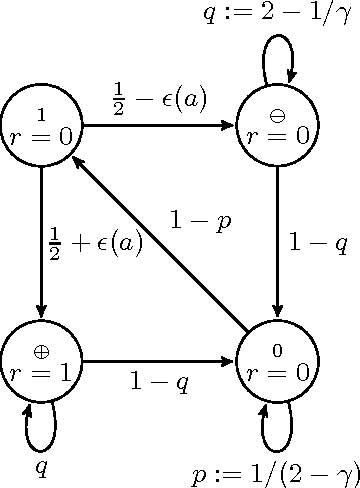
We present a new algorithm for general reinforcement learning where the true environment is known to belong to a finite class of N arbitrary models. The algorithm is shown to be near-optimal for all but O(N log^2 N) time-steps with high probability. Infinite classes are also considered where we show that compactness is a key criterion for determining the existence of uniform sample-complexity bounds. A matching lower bound is given for the finite case.

Concentration and Confidence for Discrete Bayesian Sequence Predictors

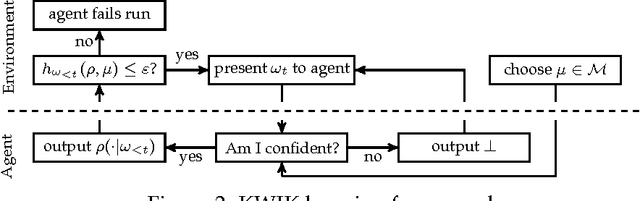
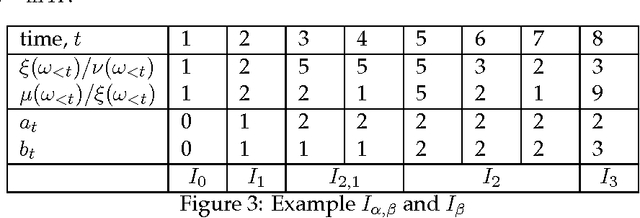
Bayesian sequence prediction is a simple technique for predicting future symbols sampled from an unknown measure on infinite sequences over a countable alphabet. While strong bounds on the expected cumulative error are known, there are only limited results on the distribution of this error. We prove tight high-probability bounds on the cumulative error, which is measured in terms of the Kullback-Leibler (KL) divergence. We also consider the problem of constructing upper confidence bounds on the KL and Hellinger errors similar to those constructed from Hoeffding-like bounds in the i.i.d. case. The new results are applied to show that Bayesian sequence prediction can be used in the Knows What It Knows (KWIK) framework with bounds that match the state-of-the-art.

PAC Bounds for Discounted MDPs

We study upper and lower bounds on the sample-complexity of learning near-optimal behaviour in finite-state discounted Markov Decision Processes (MDPs). For the upper bound we make the assumption that each action leads to at most two possible next-states and prove a new bound for a UCRL-style algorithm on the number of time-steps when it is not Probably Approximately Correct (PAC). The new lower bound strengthens previous work by being both more general (it applies to all policies) and tighter. The upper and lower bounds match up to logarithmic factors.

No Free Lunch versus Occam's Razor in Supervised Learning

The No Free Lunch theorems are often used to argue that domain specific knowledge is required to design successful algorithms. We use algorithmic information theory to argue the case for a universal bias allowing an algorithm to succeed in all interesting problem domains. Additionally, we give a new algorithm for off-line classification, inspired by Solomonoff induction, with good performance on all structured problems under reasonable assumptions. This includes a proof of the efficacy of the well-known heuristic of randomly selecting training data in the hope of reducing misclassification rates.

Asymptotically Optimal Agents

Artificial general intelligence aims to create agents capable of learning to solve arbitrary interesting problems. We define two versions of asymptotic optimality and prove that no agent can satisfy the strong version while in some cases, depending on discounting, there does exist a non-computable weak asymptotically optimal agent.

Universal Prediction of Selected Bits

Many learning tasks can be viewed as sequence prediction problems. For example, online classification can be converted to sequence prediction with the sequence being pairs of input/target data and where the goal is to correctly predict the target data given input data and previous input/target pairs. Solomonoff induction is known to solve the general sequence prediction problem, but only if the entire sequence is sampled from a computable distribution. In the case of classification and discriminative learning though, only the targets need be structured (given the inputs). We show that the normalised version of Solomonoff induction can still be used in this case, and more generally that it can detect any recursive sub-pattern (regularity) within an otherwise completely unstructured sequence. It is also shown that the unnormalised version can fail to predict very simple recursive sub-patterns.

Time Consistent Discounting

A possibly immortal agent tries to maximise its summed discounted rewards over time, where discounting is used to avoid infinite utilities and encourage the agent to value current rewards more than future ones. Some commonly used discount functions lead to time-inconsistent behavior where the agent changes its plan over time. These inconsistencies can lead to very poor behavior. We generalise the usual discounted utility model to one where the discount function changes with the age of the agent. We then give a simple characterisation of time-(in)consistent discount functions and show the existence of a rational policy for an agent that knows its discount function is time-inconsistent.