Random Rank: The One and Only Strategyproof and Proportionally Fair Randomized Facility Location Mechanism

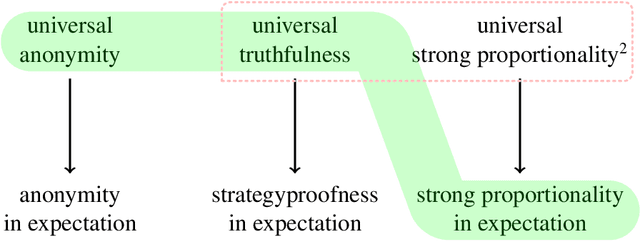
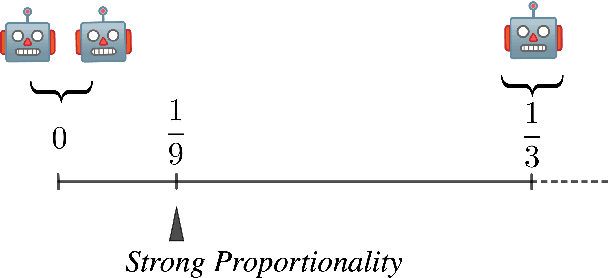
Proportionality is an attractive fairness concept that has been applied to a range of problems including the facility location problem, a classic problem in social choice. In our work, we propose a concept called Strong Proportionality, which ensures that when there are two groups of agents at different locations, both groups incur the same total cost. We show that although Strong Proportionality is a well-motivated and basic axiom, there is no deterministic strategyproof mechanism satisfying the property. We then identify a randomized mechanism called Random Rank (which uniformly selects a number $k$ between $1$ to $n$ and locates the facility at the $k$'th highest agent location) which satisfies Strong Proportionality in expectation. Our main theorem characterizes Random Rank as the unique mechanism that achieves universal truthfulness, universal anonymity, and Strong Proportionality in expectation among all randomized mechanisms. Finally, we show via the AverageOrRandomRank mechanism that even stronger ex-post fairness guarantees can be achieved by weakening universal truthfulness to strategyproofness in expectation.

The Meta-Turing Test

We propose an alternative to the Turing test that removes the inherent asymmetry between humans and machines in Turing's original imitation game. In this new test, both humans and machines judge each other. We argue that this makes the test more robust against simple deceptions. We also propose a small number of refinements to improve further the test. These refinements could be applied also to Turing's original imitation game.

Fairness Amidst Non-IID Graph Data: A Literature Review

Fairness in machine learning (ML), the process to understand and correct algorithmic bias, has gained increasing attention with numerous literature being carried out, commonly assume the underlying data is independent and identically distributed (IID). On the other hand, graphs are a ubiquitous data structure to capture connections among individual units and is non-IID by nature. It is therefore of great importance to bridge the traditional fairness literature designed on IID data and ubiquitous non-IID graph representations to tackle bias in ML systems. In this survey, we review such recent advance in fairness amidst non-IID graph data and identify datasets and evaluation metrics available for future research. We also point out the limitations of existing work as well as promising future directions.

Strategyproof and Proportionally Fair Facility Location

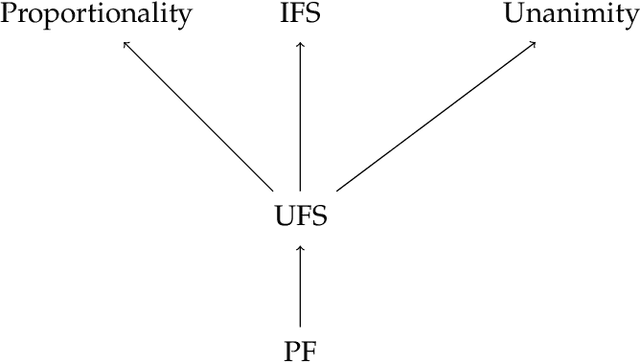
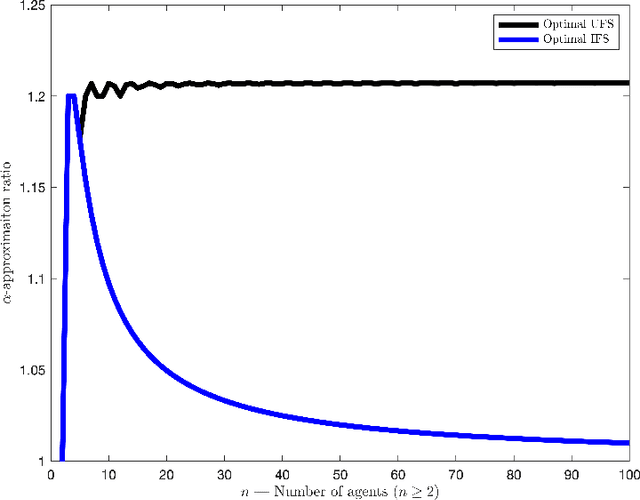
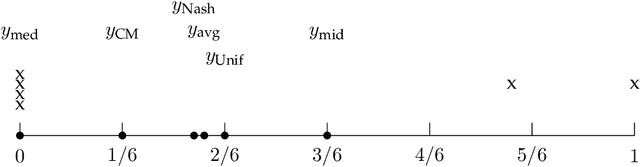
We focus on a simple, one-dimensional collective decision problem (often referred to as the facility location problem) and explore issues of strategyproofness and proportional fairness. We present several characterization results for mechanisms that satisfy strategyproofness and varying levels of proportional fairness. We also characterize one of the mechanisms as the unique equilibrium outcome for any mechanism that satisfies natural fairness and monotonicity properties. Finally, we identify strategyproof and proportionally fair mechanisms that provide the best welfare-optimal approximation among all mechanisms that satisfy the corresponding fairness axiom.

Strategy Proof Mechanisms for Facility Location with Capacity Limits

An important feature of many real world facility location problems are capacity limits on the facilities. We show here how capacity constraints make it harder to design strategy proof mechanisms for facility location, but counter-intuitively can improve the guarantees on how well we can approximate the optimal solution.

Strategy Proof Mechanisms for Facility Location in Euclidean and Manhattan Space

We study the impact on mechanisms for facility location of moving from one dimension to two (or more) dimensions and Euclidean or Manhattan distances. We consider three fundamental axiomatic properties: anonymity which is a basic fairness property, Pareto optimality which is one of the most important efficiency properties, and strategy proofness which ensures agents do not have an incentive to mis-report. We also consider how well such mechanisms can approximate the optimal welfare. Our results are somewhat negative. Moving from one dimension to two (or more) dimensions often makes these axiomatic properties more difficult to achieve. For example, with two facilities in Euclidean space or with just a single facility in Manhattan space, no mechanism is anonymous, Pareto optimal and strategy proof. By contrast, mechanisms on the line exist with all three properties.We also show that approximation ratios may increase when moving to two (or more) dimensions. All our impossibility results are minimal. If we drop one of the three axioms (anonymity, Pareto optimality or strategy proofness) multiple mechanisms satisfy the other two axioms.

Strategy Proof Mechanisms for Facility Location at Limited Locations

Facility location problems often permit facilities to be located at any position. But what if this is not the case in practice? What if facilities can only be located at particular locations like a highway exit or close to a bus stop? We consider here the impact of such constraints on the location of facilities on the performance of strategy proof mechanisms for locating facilities.We study four different performance objectives: the total distance agents must travel to their closest facility, the maximum distance any agent must travel to their closest facility, and the utilitarian and egalitarian welfare.We show that constraining facilities to a limited set of locations makes all four objectives harder to approximate in general.

Adventures in Mathematical Reasoning

"Mathematics is not a careful march down a well-cleared highway, but a journey into a strange wilderness, where the explorers often get lost. Rigour should be a signal to the historian that the maps have been made, and the real explorers have gone elsewhere." W.S. Anglin, the Mathematical Intelligencer, 4 (4), 1982.

On the Complexity of Breaking Symmetry

We can break symmetry by eliminating solutions within a symmetry class that are not least in the lexicographical ordering. This is often referred to as the lex-leader method. Unfortunately, as symmetry groups can be large, the lexleader method is not tractable in general. We prove that using other total orderings besides the usual lexicographical ordering will not reduce the computational complexity of breaking symmetry in general. It follows that breaking symmetry with other orderings like the Gray code ordering or the Snake-Lex ordering is intractable in general.

Fair Division: The Computer Scientist's Perspective

I survey recent progress on a classic and challenging problem in social choice: the fair division of indivisible items. I discuss how a computational perspective has provided interesting insights into and understanding of how to divide items fairly and efficiently. This has involved bringing to bear tools such as those used in knowledge representation, computational complexity, approximation methods, game theory, online analysis and communication complexity