Group Fairness in Peer Review

Large conferences such as NeurIPS and AAAI serve as crossroads of various AI fields, since they attract submissions from a vast number of communities. However, in some cases, this has resulted in a poor reviewing experience for some communities, whose submissions get assigned to less qualified reviewers outside of their communities. An often-advocated solution is to break up any such large conference into smaller conferences, but this can lead to isolation of communities and harm interdisciplinary research. We tackle this challenge by introducing a notion of group fairness, called the core, which requires that every possible community (subset of researchers) to be treated in a way that prevents them from unilaterally benefiting by withdrawing from a large conference. We study a simple peer review model, prove that it always admits a reviewing assignment in the core, and design an efficient algorithm to find one such assignment. We use real data from CVPR and ICLR conferences to compare our algorithm to existing reviewing assignment algorithms on a number of metrics.

REVEAL-IT: REinforcement learning with Visibility of Evolving Agent poLicy for InTerpretability

Understanding the agent's learning process, particularly the factors that contribute to its success or failure post-training, is crucial for comprehending the rationale behind the agent's decision-making process. Prior methods clarify the learning process by creating a structural causal model (SCM) or visually representing the distribution of value functions. Nevertheless, these approaches have constraints as they exclusively function in 2D-environments or with uncomplicated transition dynamics. Understanding the agent's learning process in complicated environments or tasks is more challenging. In this paper, we propose REVEAL-IT, a novel framework for explaining the learning process of an agent in complex environments. Initially, we visualize the policy structure and the agent's learning process for various training tasks. By visualizing these findings, we can understand how much a particular training task or stage affects the agent's performance in test. Then, a GNN-based explainer learns to highlight the most important section of the policy, providing a more clear and robust explanation of the agent's learning process. The experiments demonstrate that explanations derived from this framework can effectively help in the optimization of the

Nash Welfare and Facility Location

We consider the problem of locating a facility to serve a set of agents located along a line. The Nash welfare objective function, defined as the product of the agents' utilities, is known to provide a compromise between fairness and efficiency in resource allocation problems. We apply this welfare notion to the facility location problem, converting individual costs to utilities and analyzing the facility placement that maximizes the Nash welfare. We give a polynomial-time approximation algorithm to compute this facility location, and prove results suggesting that it achieves a good balance of fairness and efficiency. Finally, we take a mechanism design perspective and propose a strategy-proof mechanism with a bounded approximation ratio for Nash welfare.

Proportionally Representative Clustering

In recent years, there has been a surge in effort to formalize notions of fairness in machine learning. We focus on clustering -- one of the fundamental tasks in unsupervised machine learning. We propose a new axiom that captures proportional representation fairness (PRF). We make a case that the concept achieves the raison d'{\^{e}}tre of several existing concepts in the literature in an arguably more convincing manner. Our fairness concept is not satisfied by existing fair clustering algorithms. We design efficient algorithms to achieve PRF both for unconstrained and discrete clustering problems.

Proportional Fairness in Obnoxious Facility Location

We consider the obnoxious facility location problem (in which agents prefer the facility location to be far from them) and propose a hierarchy of distance-based proportional fairness concepts for the problem. These fairness axioms ensure that groups of agents at the same location are guaranteed to be a distance from the facility proportional to their group size. We consider deterministic and randomized mechanisms, and compute tight bounds on the price of proportional fairness. In the deterministic setting, not only are our proportional fairness axioms incompatible with strategyproofness, the Nash equilibria may not guarantee welfare within a constant factor of the optimal welfare. On the other hand, in the randomized setting, we identify proportionally fair and strategyproof mechanisms that give an expected welfare within a constant factor of the optimal welfare.

Task Allocation using a Team of Robots

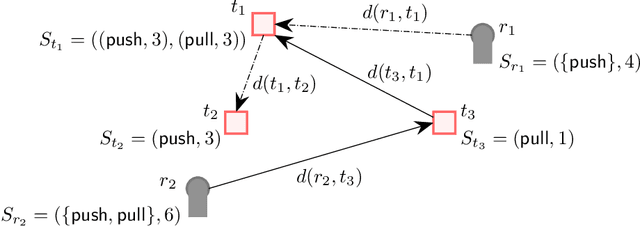
Task allocation using a team or coalition of robots is one of the most important problems in robotics, computer science, operational research, and artificial intelligence. In recent work, research has focused on handling complex objectives and feasibility constraints amongst other variations of the multi-robot task allocation problem. There are many examples of important research progress in these directions. We present a general formulation of the task allocation problem that generalizes several versions that are well-studied. Our formulation includes the states of robots, tasks, and the surrounding environment in which they operate. We describe how the problem can vary depending on the feasibility constraints, objective functions, and the level of dynamically changing information. In addition, we discuss existing solution approaches for the problem including optimization-based approaches, and market-based approaches.

Random Rank: The One and Only Strategyproof and Proportionally Fair Randomized Facility Location Mechanism

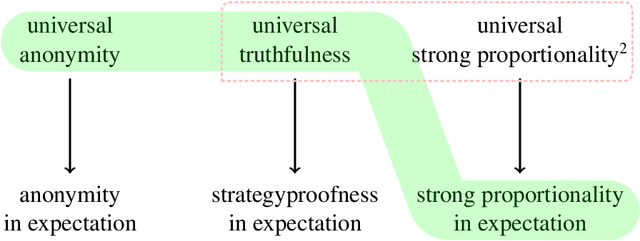
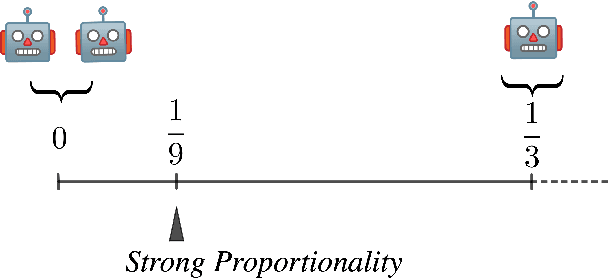
Proportionality is an attractive fairness concept that has been applied to a range of problems including the facility location problem, a classic problem in social choice. In our work, we propose a concept called Strong Proportionality, which ensures that when there are two groups of agents at different locations, both groups incur the same total cost. We show that although Strong Proportionality is a well-motivated and basic axiom, there is no deterministic strategyproof mechanism satisfying the property. We then identify a randomized mechanism called Random Rank (which uniformly selects a number $k$ between $1$ to $n$ and locates the facility at the $k$'th highest agent location) which satisfies Strong Proportionality in expectation. Our main theorem characterizes Random Rank as the unique mechanism that achieves universal truthfulness, universal anonymity, and Strong Proportionality in expectation among all randomized mechanisms. Finally, we show via the AverageOrRandomRank mechanism that even stronger ex-post fairness guarantees can be achieved by weakening universal truthfulness to strategyproofness in expectation.

Obvious Manipulability of Voting Rules

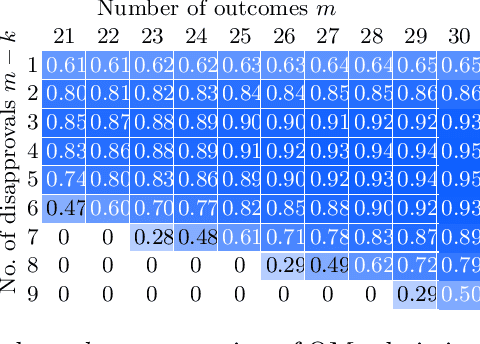
The Gibbard-Satterthwaite theorem states that no unanimous and non-dictatorial voting rule is strategyproof. We revisit voting rules and consider a weaker notion of strategyproofness called not obvious manipulability that was proposed by Troyan and Morrill (2020). We identify several classes of voting rules that satisfy this notion. We also show that several voting rules including k-approval fail to satisfy this property. We characterize conditions under which voting rules are obviously manipulable. One of our insights is that certain rules are obviously manipulable when the number of alternatives is relatively large compared to the number of voters. In contrast to the Gibbard-Satterthwaite theorem, many of the rules we examined are not obviously manipulable. This reflects the relatively easier satisfiability of the notion and the zero information assumption of not obvious manipulability, as opposed to the perfect information assumption of strategyproofness. We also present algorithmic results for computing obvious manipulations and report on experiments.

Strategyproof and Proportionally Fair Facility Location

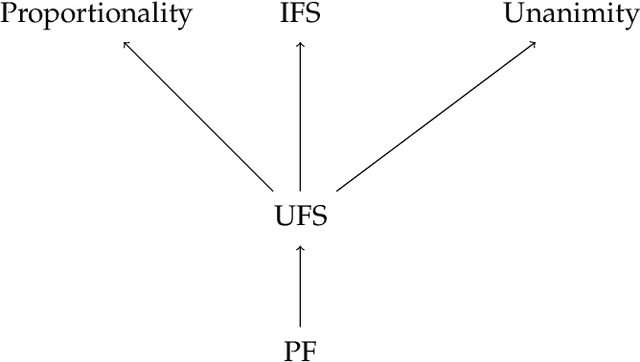
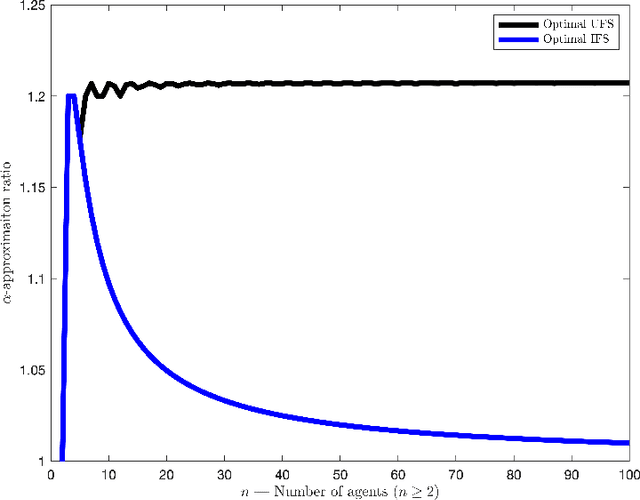
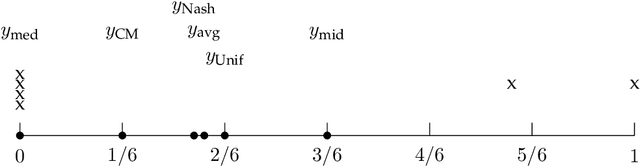
We focus on a simple, one-dimensional collective decision problem (often referred to as the facility location problem) and explore issues of strategyproofness and proportional fairness. We present several characterization results for mechanisms that satisfy strategyproofness and varying levels of proportional fairness. We also characterize one of the mechanisms as the unique equilibrium outcome for any mechanism that satisfies natural fairness and monotonicity properties. Finally, we identify strategyproof and proportionally fair mechanisms that provide the best welfare-optimal approximation among all mechanisms that satisfy the corresponding fairness axiom.

Multi-Robot Task Allocation -- Complexity and Approximation

Multi-robot task allocation is one of the most fundamental classes of problems in robotics and is crucial for various real-world robotic applications such as search, rescue and area exploration. We consider the Single-Task robots and Multi-Robot tasks Instantaneous Assignment (ST-MR-IA) setting where each task requires at least a certain number of robots and each robot can work on at most one task and incurs an operational cost for each task. Our aim is to consider a natural computational problem of allocating robots to complete the maximum number of tasks subject to budget constraints. We consider budget constraints of three different kinds: (1) total budget, (2) task budget, and (3) robot budget. We provide a detailed complexity analysis including results on approximations as well as polynomial-time algorithms for the general setting and important restricted settings.