On the expressiveness and spectral bias of KANs

Kolmogorov-Arnold Networks (KAN) \cite{liu2024kan} were very recently proposed as a potential alternative to the prevalent architectural backbone of many deep learning models, the multi-layer perceptron (MLP). KANs have seen success in various tasks of AI for science, with their empirical efficiency and accuracy demostrated in function regression, PDE solving, and many more scientific problems. In this article, we revisit the comparison of KANs and MLPs, with emphasis on a theoretical perspective. On the one hand, we compare the representation and approximation capabilities of KANs and MLPs. We establish that MLPs can be represented using KANs of a comparable size. This shows that the approximation and representation capabilities of KANs are at least as good as MLPs. Conversely, we show that KANs can be represented using MLPs, but that in this representation the number of parameters increases by a factor of the KAN grid size. This suggests that KANs with a large grid size may be more efficient than MLPs at approximating certain functions. On the other hand, from the perspective of learning and optimization, we study the spectral bias of KANs compared with MLPs. We demonstrate that KANs are less biased toward low frequencies than MLPs. We highlight that the multi-level learning feature specific to KANs, i.e. grid extension of splines, improves the learning process for high-frequency components. Detailed comparisons with different choices of depth, width, and grid sizes of KANs are made, shedding some light on how to choose the hyperparameters in practice.

KAN: Kolmogorov-Arnold Networks

Inspired by the Kolmogorov-Arnold representation theorem, we propose Kolmogorov-Arnold Networks (KANs) as promising alternatives to Multi-Layer Perceptrons (MLPs). While MLPs have fixed activation functions on nodes ("neurons"), KANs have learnable activation functions on edges ("weights"). KANs have no linear weights at all -- every weight parameter is replaced by a univariate function parametrized as a spline. We show that this seemingly simple change makes KANs outperform MLPs in terms of accuracy and interpretability. For accuracy, much smaller KANs can achieve comparable or better accuracy than much larger MLPs in data fitting and PDE solving. Theoretically and empirically, KANs possess faster neural scaling laws than MLPs. For interpretability, KANs can be intuitively visualized and can easily interact with human users. Through two examples in mathematics and physics, KANs are shown to be useful collaborators helping scientists (re)discover mathematical and physical laws. In summary, KANs are promising alternatives for MLPs, opening opportunities for further improving today's deep learning models which rely heavily on MLPs.

Asymptotic Escape of Spurious Critical Points on the Low-rank Matrix Manifold

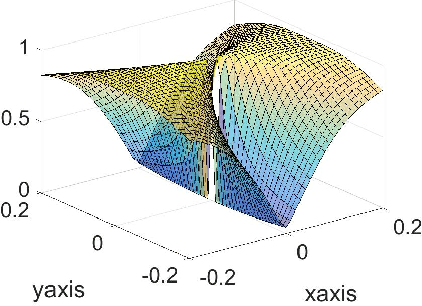
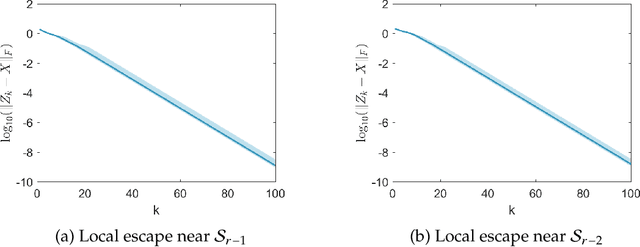
We show that the Riemannian gradient descent algorithm on the low-rank matrix manifold almost surely escapes some spurious critical points on the boundary of the manifold. Given that the low-rank matrix manifold is an incomplete set, this result is the first to overcome this difficulty and partially justify the global use of the Riemannian gradient descent on the manifold. The spurious critical points are some rank-deficient matrices that capture only part of the SVD components of the ground truth. They exhibit very singular behavior and evade the classical analysis of strict saddle points. We show that using the dynamical low-rank approximation and a rescaled gradient flow, some of the spurious critical points can be converted to classical strict saddle points, which leads to the desired result. Numerical experiments are provided to support our theoretical findings.

Multiscale Invertible Generative Networks for High-Dimensional Bayesian Inference

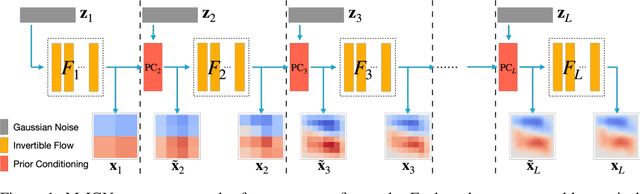
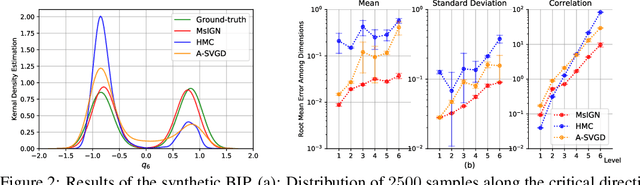
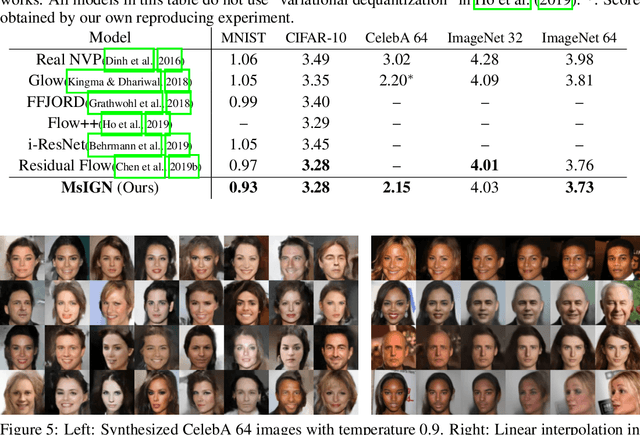
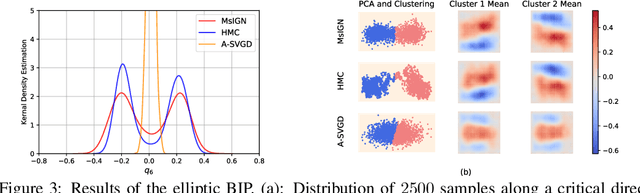
We propose a Multiscale Invertible Generative Network (MsIGN) and associated training algorithm that leverages multiscale structure to solve high-dimensional Bayesian inference. To address the curse of dimensionality, MsIGN exploits the low-dimensional nature of the posterior, and generates samples from coarse to fine scale (low to high dimension) by iteratively upsampling and refining samples. MsIGN is trained in a multi-stage manner to minimize the Jeffreys divergence, which avoids mode dropping in high-dimensional cases. On two high-dimensional Bayesian inverse problems, we show superior performance of MsIGN over previous approaches in posterior approximation and multiple mode capture. On the natural image synthesis task, MsIGN achieves superior performance in bits-per-dimension over baseline models and yields great interpret-ability of its neurons in intermediate layers.

Fast Global Convergence for Low-rank Matrix Recovery via Riemannian Gradient Descent with Random Initialization

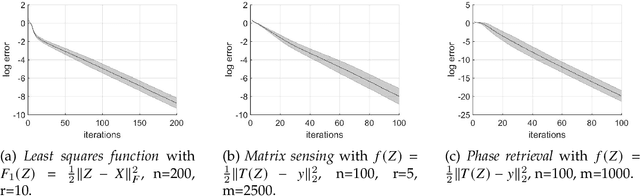
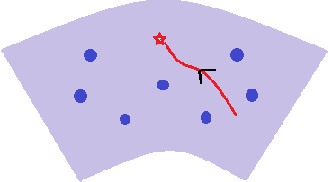
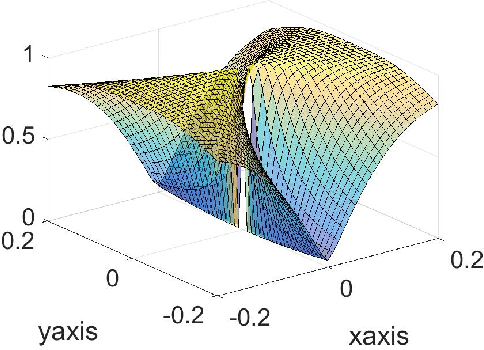
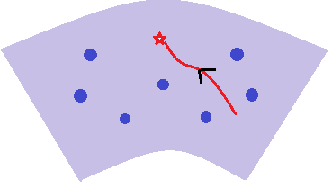
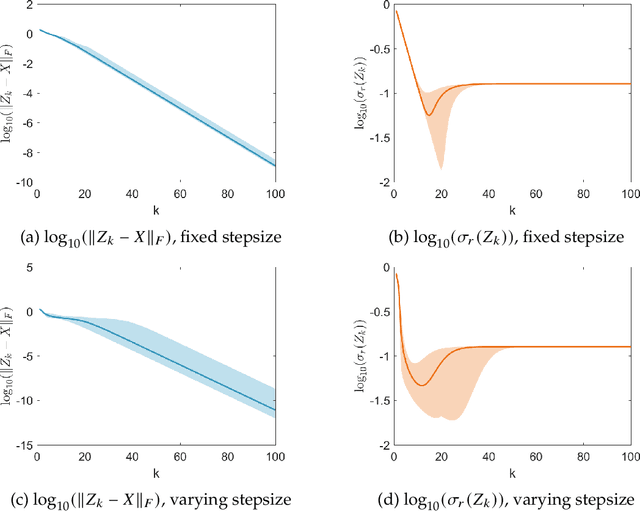
In this paper, we propose a new global analysis framework for a class of low-rank matrix recovery problems on the Riemannian manifold. We analyze the global behavior for the Riemannian optimization with random initialization. We use the Riemannian gradient descent algorithm to minimize a least squares loss function, and study the asymptotic behavior as well as the exact convergence rate. We reveal a previously unknown geometric property of the low-rank matrix manifold, which is the existence of spurious critical points for the simple least squares function on the manifold. We show that under some assumptions, the Riemannian gradient descent starting from a random initialization with high probability avoids these spurious critical points and only converges to the ground truth in nearly linear convergence rate, i.e. $\mathcal{O}(\text{log}(\frac{1}{\epsilon})+ \text{log}(n))$ iterations to reach an $\epsilon$-accurate solution. We use two applications as examples for our global analysis. The first one is a rank-1 matrix recovery problem. The second one is the Gaussian phase retrieval problem. The second example only satisfies the weak isometry property, but has behavior similar to that of the first one except for an extra saddle set. Our convergence guarantee is nearly optimal and almost dimension-free, which fully explains the numerical observations. The global analysis can be potentially extended to other data problems with random measurement structures and empirical least squares loss functions.

A Fast Hierarchically Preconditioned Eigensolver Based On Multiresolution Matrix Decomposition

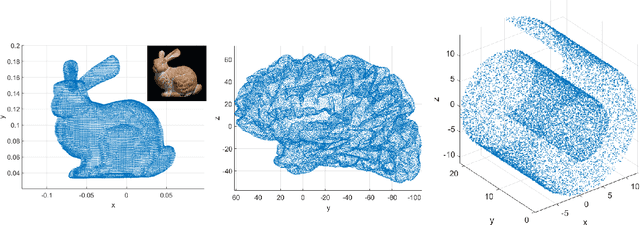
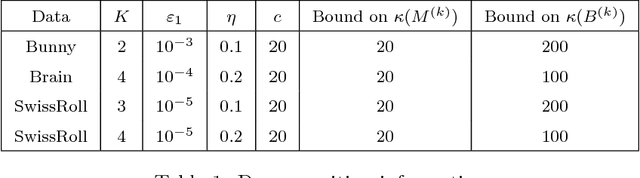
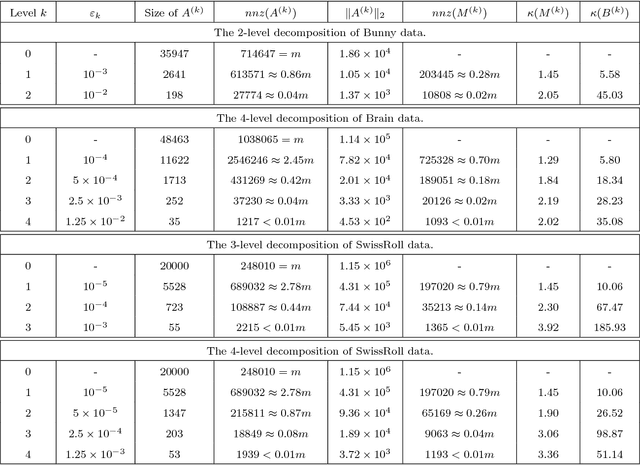
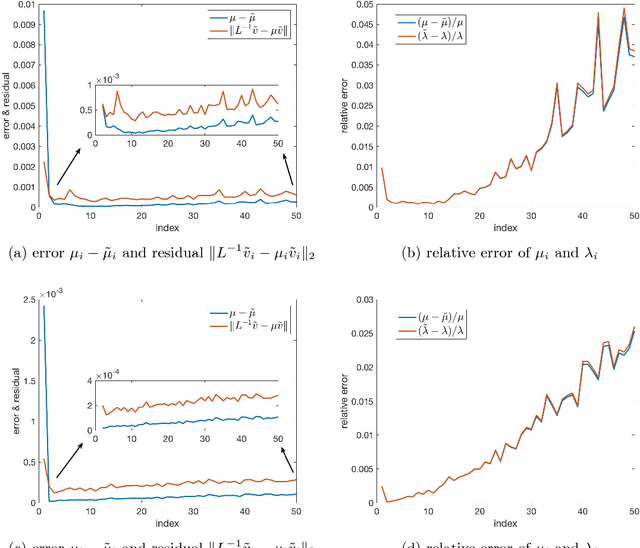
In this paper we propose a new iterative method to hierarchically compute a relatively large number of leftmost eigenpairs of a sparse symmetric positive matrix under the multiresolution operator compression framework. We exploit the well-conditioned property of every decomposition components by integrating the multiresolution framework into the Implicitly restarted Lanczos method. We achieve this combination by proposing an extension-refinement iterative scheme, in which the intrinsic idea is to decompose the target spectrum into several segments such that the corresponding eigenproblem in each segment is well-conditioned. Theoretical analysis and numerical illustration are also reported to illustrate the efficiency and effectiveness of this algorithm.