Learning Gradually Non-convex Image Priors Using Score Matching

In this paper, we propose a unified framework of denoising score-based models in the context of graduated non-convex energy minimization. We show that for sufficiently large noise variance, the associated negative log density -- the energy -- becomes convex. Consequently, denoising score-based models essentially follow a graduated non-convexity heuristic. We apply this framework to learning generalized Fields of Experts image priors that approximate the joint density of noisy images and their associated variances. These priors can be easily incorporated into existing optimization algorithms for solving inverse problems and naturally implement a fast and robust graduated non-convexity mechanism.

Explicit Diffusion of Gaussian Mixture Model Based Image Priors

In this work we tackle the problem of estimating the density $f_X$ of a random variable $X$ by successive smoothing, such that the smoothed random variable $Y$ fulfills $(\partial_t - \Delta_1)f_Y(\,\cdot\,, t) = 0$, $f_Y(\,\cdot\,, 0) = f_X$. With a focus on image processing, we propose a product/fields of experts model with Gaussian mixture experts that admits an analytic expression for $f_Y (\,\cdot\,, t)$ under an orthogonality constraint on the filters. This construction naturally allows the model to be trained simultaneously over the entire diffusion horizon using empirical Bayes. We show preliminary results on image denoising where our model leads to competitive results while being tractable, interpretable, and having only a small number of learnable parameters. As a byproduct, our model can be used for reliable noise estimation, allowing blind denoising of images corrupted by heteroscedastic noise.

Posterior-Variance-Based Error Quantification for Inverse Problems in Imaging

In this work, a method for obtaining pixel-wise error bounds in Bayesian regularization of inverse imaging problems is introduced. The proposed method employs estimates of the posterior variance together with techniques from conformal prediction in order to obtain coverage guarantees for the error bounds, without making any assumption on the underlying data distribution. It is generally applicable to Bayesian regularization approaches, independent, e.g., of the concrete choice of the prior. Furthermore, the coverage guarantees can also be obtained in case only approximate sampling from the posterior is possible. With this in particular, the proposed framework is able to incorporate any learned prior in a black-box manner. Guaranteed coverage without assumptions on the underlying distributions is only achievable since the magnitude of the error bounds is, in general, unknown in advance. Nevertheless, experiments with multiple regularization approaches presented in the paper confirm that in practice, the obtained error bounds are rather tight. For realizing the numerical experiments, also a novel primal-dual Langevin algorithm for sampling from non-smooth distributions is introduced in this work.

Stable deep MRI reconstruction using Generative Priors

Data-driven approaches recently achieved remarkable success in medical image reconstruction, but integration into clinical routine remains challenging due to a lack of generalizability and interpretability. Existing approaches usually require high-quality data-image pairs for training, but such data is not easily available for any imaging protocol and the reconstruction quality can quickly degrade even if only minor changes are made to the protocol. In addition, data-driven methods may create artificial features that can influence the clinicians decision-making. This is unacceptable if the clinician is unaware of the uncertainty associated with the reconstruction. In this paper, we address these challenges in a unified framework based on generative image priors. We propose a novel deep neural network based regularizer which is trained in an unsupervised setting on reference images without requiring any data-image pairs. After training, the regularizer can be used as part of a classical variational approach in combination with any acquisition protocols and shows stable behavior even if the test data deviates significantly from the training data. Furthermore, our probabilistic interpretation provides a distribution of reconstructions and hence allows uncertainty quantification. We demonstrate our approach on parallel magnetic resonance imaging, where results show competitive performance with SotA end-to-end deep learning methods, while preserving the flexibility of the acquisition protocol and allowing for uncertainty quantification.

Is Appearance Free Action Recognition Possible?

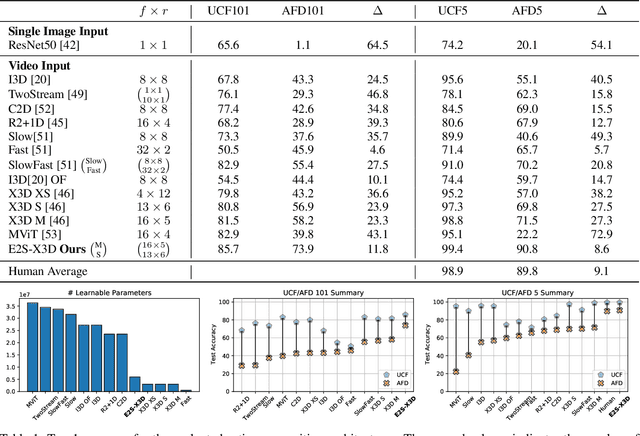
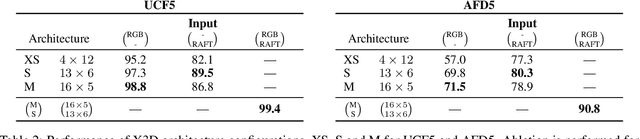
Intuition might suggest that motion and dynamic information are key to video-based action recognition. In contrast, there is evidence that state-of-the-art deep-learning video understanding architectures are biased toward static information available in single frames. Presently, a methodology and corresponding dataset to isolate the effects of dynamic information in video are missing. Their absence makes it difficult to understand how well contemporary architectures capitalize on dynamic vs. static information. We respond with a novel Appearance Free Dataset (AFD) for action recognition. AFD is devoid of static information relevant to action recognition in a single frame. Modeling of the dynamics is necessary for solving the task, as the action is only apparent through consideration of the temporal dimension. We evaluated 11 contemporary action recognition architectures on AFD as well as its related RGB video. Our results show a notable decrease in performance for all architectures on AFD compared to RGB. We also conducted a complimentary study with humans that shows their recognition accuracy on AFD and RGB is very similar and much better than the evaluated architectures on AFD. Our results motivate a novel architecture that revives explicit recovery of optical flow, within a contemporary design for best performance on AFD and RGB.

Computed Tomography Reconstruction using Generative Energy-Based Priors

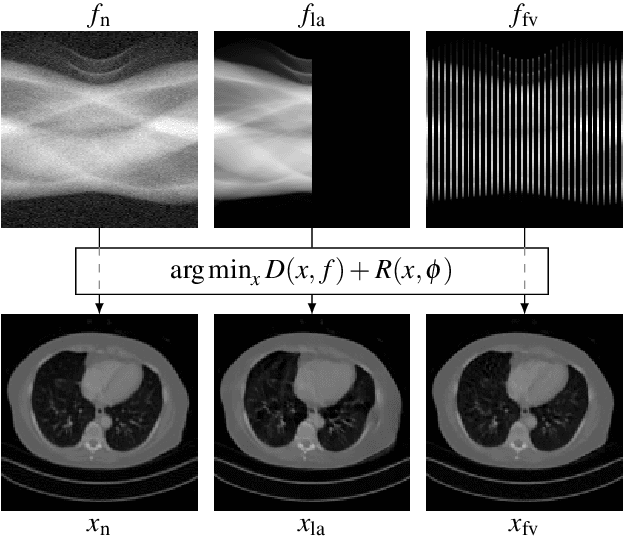
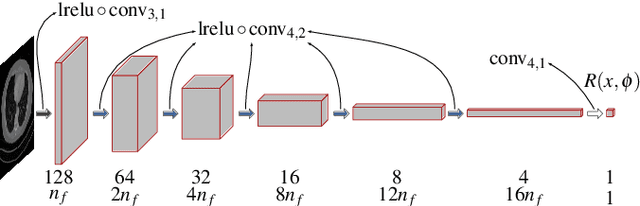
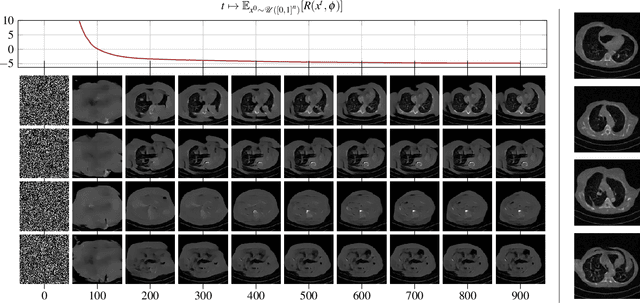
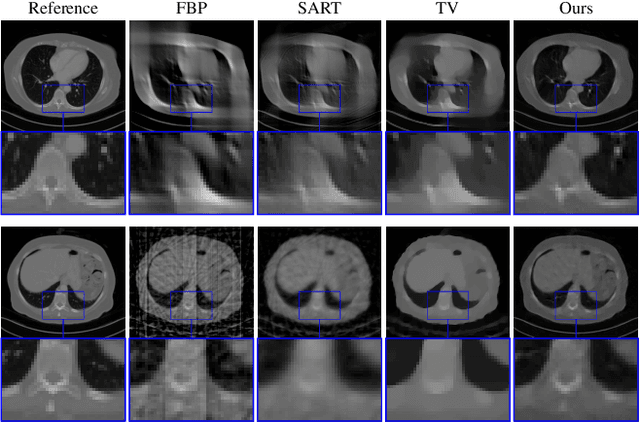
In the past decades, Computed Tomography (CT) has established itself as one of the most important imaging techniques in medicine. Today, the applicability of CT is only limited by the deposited radiation dose, reduction of which manifests in noisy or incomplete measurements. Thus, the need for robust reconstruction algorithms arises. In this work, we learn a parametric regularizer with a global receptive field by maximizing it's likelihood on reference CT data. Due to this unsupervised learning strategy, our trained regularizer truly represents higher-level domain statistics, which we empirically demonstrate by synthesizing CT images. Moreover, this regularizer can easily be applied to different CT reconstruction problems by embedding it in a variational framework, which increases flexibility and interpretability compared to feed-forward learning-based approaches. In addition, the accompanying probabilistic perspective enables experts to explore the full posterior distribution and may quantify uncertainty of the reconstruction approach. We apply the regularizer to limited-angle and few-view CT reconstruction problems, where it outperforms traditional reconstruction algorithms by a large margin.

Learning atrial fiber orientations and conductivity tensors from intracardiac maps using physics-informed neural networks

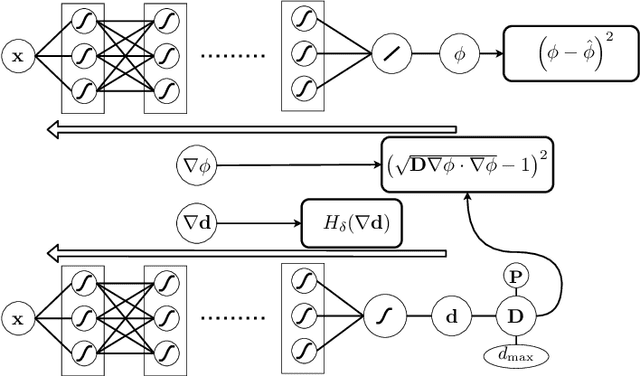
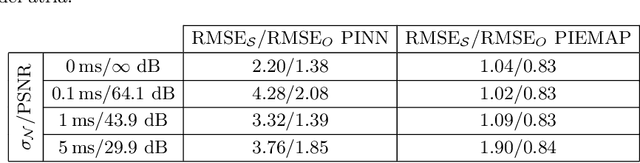
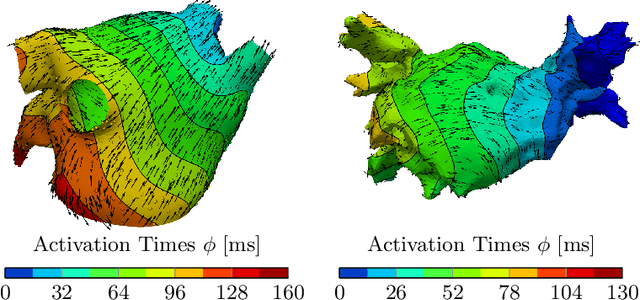
Electroanatomical maps are a key tool in the diagnosis and treatment of atrial fibrillation. Current approaches focus on the activation times recorded. However, more information can be extracted from the available data. The fibers in cardiac tissue conduct the electrical wave faster, and their direction could be inferred from activation times. In this work, we employ a recently developed approach, called physics informed neural networks, to learn the fiber orientations from electroanatomical maps, taking into account the physics of the electrical wave propagation. In particular, we train the neural network to weakly satisfy the anisotropic eikonal equation and to predict the measured activation times. We use a local basis for the anisotropic conductivity tensor, which encodes the fiber orientation. The methodology is tested both in a synthetic example and for patient data. Our approach shows good agreement in both cases and it outperforms a state of the art method in the patient data. The results show a first step towards learning the fiber orientations from electroanatomical maps with physics-informed neural networks.

Bayesian Uncertainty Estimation of Learned Variational MRI Reconstruction

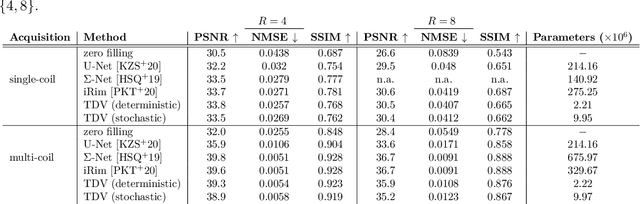
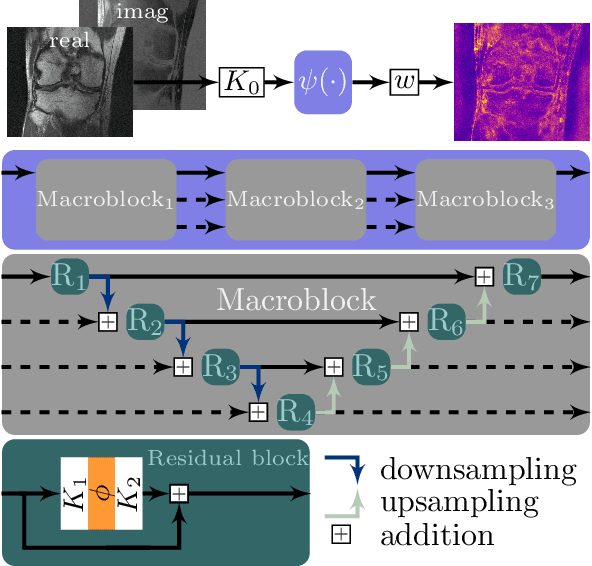
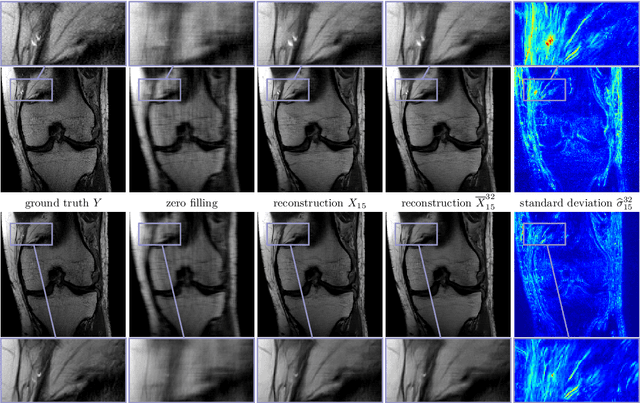
Recent deep learning approaches focus on improving quantitative scores of dedicated benchmarks, and therefore only reduce the observation-related (aleatoric) uncertainty. However, the model-immanent (epistemic) uncertainty is less frequently systematically analyzed. In this work, we introduce a Bayesian variational framework to quantify the epistemic uncertainty. To this end, we solve the linear inverse problem of undersampled MRI reconstruction in a variational setting. The associated energy functional is composed of a data fidelity term and the total deep variation (TDV) as a learned parametric regularizer. To estimate the epistemic uncertainty we draw the parameters of the TDV regularizer from a multivariate Gaussian distribution, whose mean and covariance matrix are learned in a stochastic optimal control problem. In several numerical experiments, we demonstrate that our approach yields competitive results for undersampled MRI reconstruction. Moreover, we can accurately quantify the pixelwise epistemic uncertainty, which can serve radiologists as an additional resource to visualize reconstruction reliability.

Shared Prior Learning of Energy-Based Models for Image Reconstruction

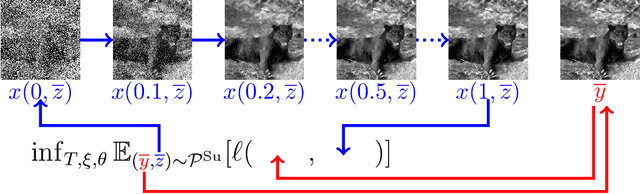
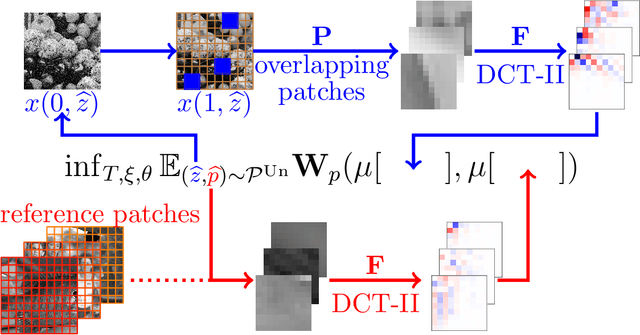
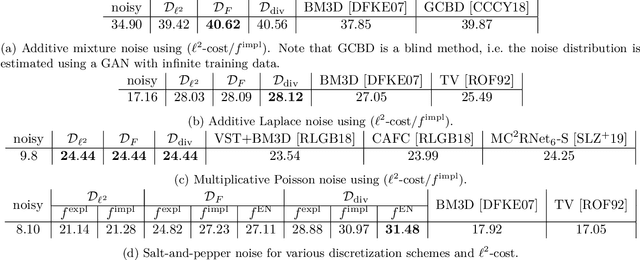
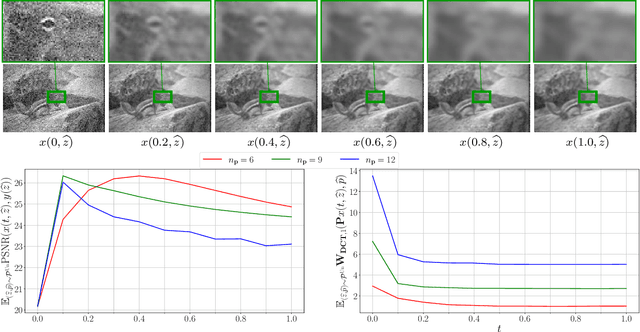
We propose a novel learning-based framework for image reconstruction particularly designed for training without ground truth data, which has three major building blocks: energy-based learning, a patch-based Wasserstein loss functional, and shared prior learning. In energy-based learning, the parameters of an energy functional composed of a learned data fidelity term and a data-driven regularizer are computed in a mean-field optimal control problem. In the absence of ground truth data, we change the loss functional to a patch-based Wasserstein functional, in which local statistics of the output images are compared to uncorrupted reference patches. Finally, in shared prior learning, both aforementioned optimal control problems are optimized simultaneously with shared learned parameters of the regularizer to further enhance unsupervised image reconstruction. We derive several time discretization schemes of the gradient flow and verify their consistency in terms of Mosco convergence. In numerous numerical experiments, we demonstrate that the proposed method generates state-of-the-art results for various image reconstruction applications--even if no ground truth images are available for training.

BP-MVSNet: Belief-Propagation-Layers for Multi-View-Stereo

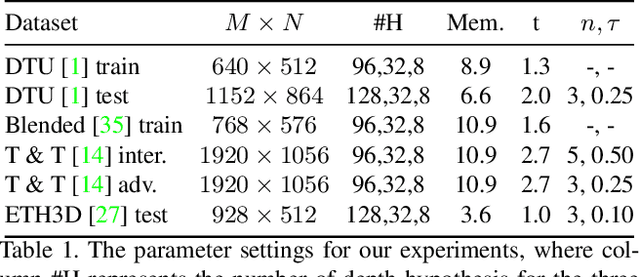
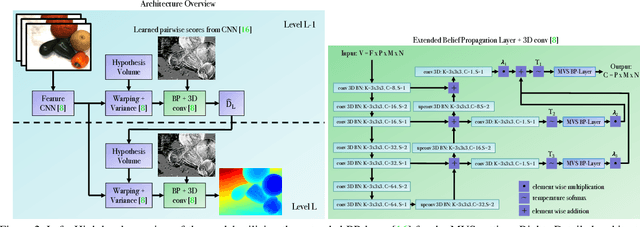
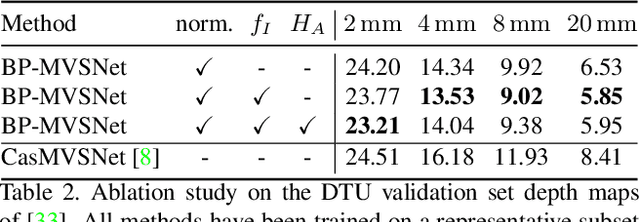
In this work, we propose BP-MVSNet, a convolutional neural network (CNN)-based Multi-View-Stereo (MVS) method that uses a differentiable Conditional Random Field (CRF) layer for regularization. To this end, we propose to extend the BP layer and add what is necessary to successfully use it in the MVS setting. We therefore show how we can calculate a normalization based on the expected 3D error, which we can then use to normalize the label jumps in the CRF. This is required to make the BP layer invariant to different scales in the MVS setting. In order to also enable fractional label jumps, we propose a differentiable interpolation step, which we embed into the computation of the pairwise term. These extensions allow us to integrate the BP layer into a multi-scale MVS network, where we continuously improve a rough initial estimate until we get high quality depth maps as a result. We evaluate the proposed BP-MVSNet in an ablation study and conduct extensive experiments on the DTU, Tanks and Temples and ETH3D data sets. The experiments show that we can significantly outperform the baseline and achieve state-of-the-art results.