Input Convex Kolmogorov Arnold Networks

This article presents an input convex neural network architecture using Kolmogorov-Arnold networks (ICKAN). Two specific networks are presented: the first is based on a low-order, linear-by-part, representation of functions, and a universal approximation theorem is provided. The second is based on cubic splines, for which only numerical results support convergence. We demonstrate on simple tests that these networks perform competitively with classical input convex neural networks (ICNNs). In a second part, we use the networks to solve some optimal transport problems needing a convex approximation of functions and demonstrate their effectiveness. Comparisons with ICNNs show that cubic ICKANs produce results similar to those of classical ICNNs.

Deep combinatorial optimisation for optimal stopping time problems and stochastic impulse control. Application to swing options pricing and fixed transaction costs options hedging

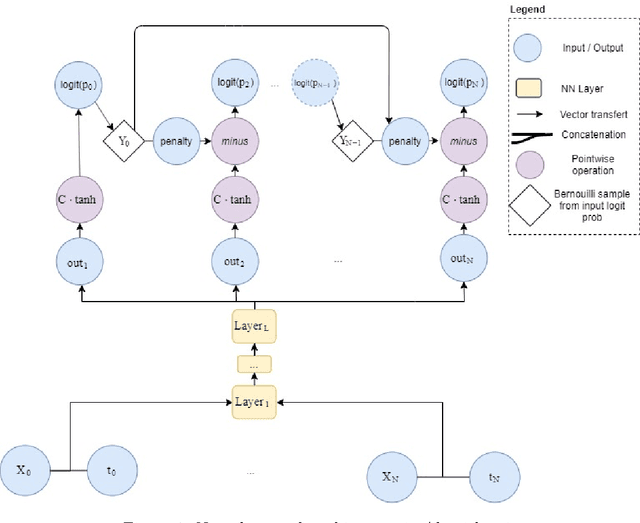
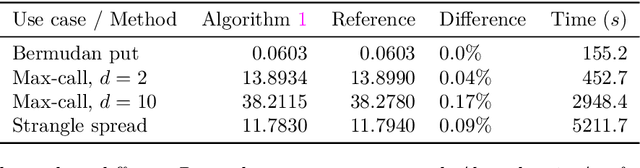
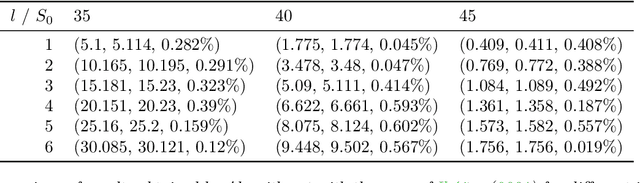
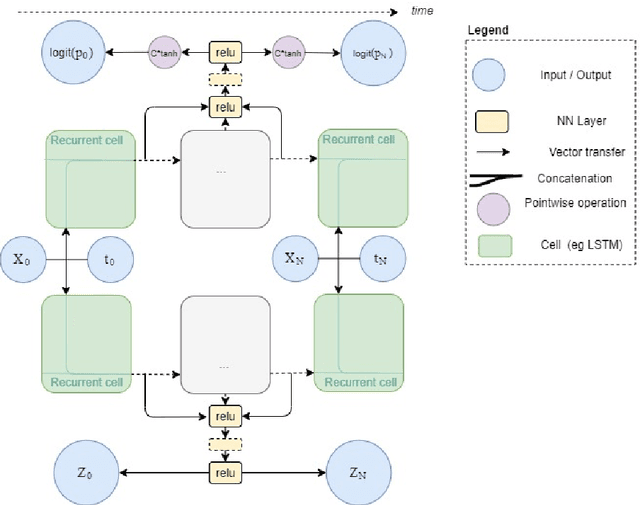
A new method for stochastic control based on neural networks and using randomisation of discrete random variables is proposed and applied to optimal stopping time problems. Numerical tests are done on the pricing of American and swing options. An extension to impulse control problems is described and applied to options hedging under fixed transaction costs. The proposed algorithms seem to be competitive with the best existing algorithms both in terms of precision and in terms of computation time.