Input Convex Kolmogorov Arnold Networks

This article presents an input convex neural network architecture using Kolmogorov-Arnold networks (ICKAN). Two specific networks are presented: the first is based on a low-order, linear-by-part, representation of functions, and a universal approximation theorem is provided. The second is based on cubic splines, for which only numerical results support convergence. We demonstrate on simple tests that these networks perform competitively with classical input convex neural networks (ICNNs). In a second part, we use the networks to solve some optimal transport problems needing a convex approximation of functions and demonstrate their effectiveness. Comparisons with ICNNs show that cubic ICKANs produce results similar to those of classical ICNNs.

New random projections for isotropic kernels using stable spectral distributions

Rahimi and Recht [31] introduced the idea of decomposing shift-invariant kernels by randomly sampling from their spectral distribution. This famous technique, known as Random Fourier Features (RFF), is in principle applicable to any shift-invariant kernel whose spectral distribution can be identified and simulated. In practice, however, it is usually applied to the Gaussian kernel because of its simplicity, since its spectral distribution is also Gaussian. Clearly, simple spectral sampling formulas would be desirable for broader classes of kernel functions. In this paper, we propose to decompose spectral kernel distributions as a scale mixture of $\alpha$-stable random vectors. This provides a simple and ready-to-use spectral sampling formula for a very large class of multivariate shift-invariant kernels, including exponential power kernels, generalized Mat\'ern kernels, generalized Cauchy kernels, as well as newly introduced kernels such as the Beta, Kummer, and Tricomi kernels. In particular, we show that the spectral densities of all these kernels are scale mixtures of the multivariate Gaussian distribution. This provides a very simple way to modify existing Random Fourier Features software based on Gaussian kernels to cover a much richer class of multivariate kernels. This result has broad applications for support vector machines, kernel ridge regression, Gaussian processes, and other kernel-based machine learning techniques for which the random Fourier features technique is applicable.

P1-KAN an effective Kolmogorov Arnold Network for function approximation

A new Kolmogorov-Arnold network (KAN) is proposed to approximate potentially irregular functions in high dimension. We show that it outperforms multilayer perceptrons in terms of accuracy and converges faster. We also compare it with ReLU-KAN, a recently proposed network: it is more time consuming than ReLU-KAN, but more accurate.

Control randomisation approach for policy gradient and application to reinforcement learning in optimal switching

We propose a comprehensive framework for policy gradient methods tailored to continuous time reinforcement learning. This is based on the connection between stochastic control problems and randomised problems, enabling applications across various classes of Markovian continuous time control problems, beyond diffusion models, including e.g. regular, impulse and optimal stopping/switching problems. By utilizing change of measure in the control randomisation technique, we derive a new policy gradient representation for these randomised problems, featuring parametrised intensity policies. We further develop actor-critic algorithms specifically designed to address general Markovian stochastic control issues. Our framework is demonstrated through its application to optimal switching problems, with two numerical case studies in the energy sector focusing on real options.

Actor critic learning algorithms for mean-field control with moment neural networks

We develop a new policy gradient and actor-critic algorithm for solving mean-field control problems within a continuous time reinforcement learning setting. Our approach leverages a gradient-based representation of the value function, employing parametrized randomized policies. The learning for both the actor (policy) and critic (value function) is facilitated by a class of moment neural network functions on the Wasserstein space of probability measures, and the key feature is to sample directly trajectories of distributions. A central challenge addressed in this study pertains to the computational treatment of an operator specific to the mean-field framework. To illustrate the effectiveness of our methods, we provide a comprehensive set of numerical results. These encompass diverse examples, including multi-dimensional settings and nonlinear quadratic mean-field control problems with controlled volatility.

Quantile and moment neural networks for learning functionals of distributions

We study news neural networks to approximate function of distributions in a probability space. Two classes of neural networks based on quantile and moment approximation are proposed to learn these functions and are theoretically supported by universal approximation theorems. By mixing the quantile and moment features in other new networks, we develop schemes that outperform existing networks on numerical test cases involving univariate distributions. For bivariate distributions, the moment neural network outperforms all other networks.

Mean-field neural networks-based algorithms for McKean-Vlasov control problems *

This paper is devoted to the numerical resolution of McKean-Vlasov control problems via the class of mean-field neural networks introduced in our companion paper [25] in order to learn the solution on the Wasserstein space. We propose several algorithms either based on dynamic programming with control learning by policy or value iteration, or backward SDE from stochastic maximum principle with global or local loss functions. Extensive numerical results on different examples are presented to illustrate the accuracy of each of our eight algorithms. We discuss and compare the pros and cons of all the tested methods.

Mean-field neural networks: learning mappings on Wasserstein space

We study the machine learning task for models with operators mapping between the Wasserstein space of probability measures and a space of functions, like e.g. in mean-field games/control problems. Two classes of neural networks, based on bin density and on cylindrical approximation, are proposed to learn these so-called mean-field functions, and are theoretically supported by universal approximation theorems. We perform several numerical experiments for training these two mean-field neural networks, and show their accuracy and efficiency in the generalization error with various test distributions. Finally, we present different algorithms relying on mean-field neural networks for solving time-dependent mean-field problems, and illustrate our results with numerical tests for the example of a semi-linear partial differential equation in the Wasserstein space of probability measures.

Discretization and Machine Learning Approximation of BSDEs with a Constraint on the Gains-Process

We study the approximation of backward stochastic differential equations (BSDEs for short) with a constraint on the gains process. We first discretize the constraint by applying a so-called facelift operator at times of a grid. We show that this discretely constrained BSDE converges to the continuously constrained one as the mesh grid converges to zero. We then focus on the approximation of the discretely constrained BSDE. For that we adopt a machine learning approach. We show that the facelift can be approximated by an optimization problem over a class of neural networks under constraints on the neural network and its derivative. We then derive an algorithm converging to the discretely constrained BSDE as the number of neurons goes to infinity. We end by numerical experiments. Mathematics Subject Classification (2010): 65C30, 65M75, 60H35, 93E20, 49L25.

Neural networks-based backward scheme for fully nonlinear PDEs

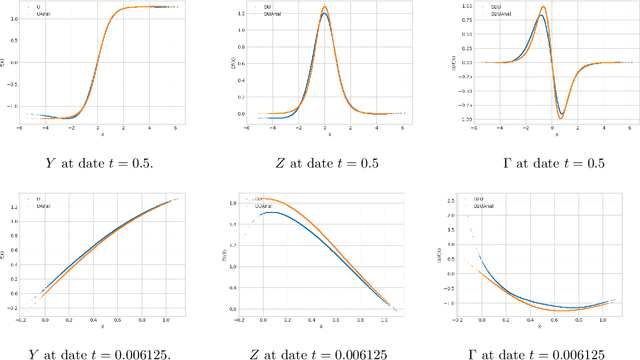
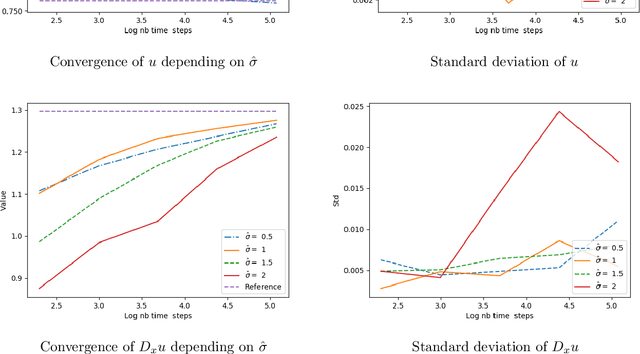
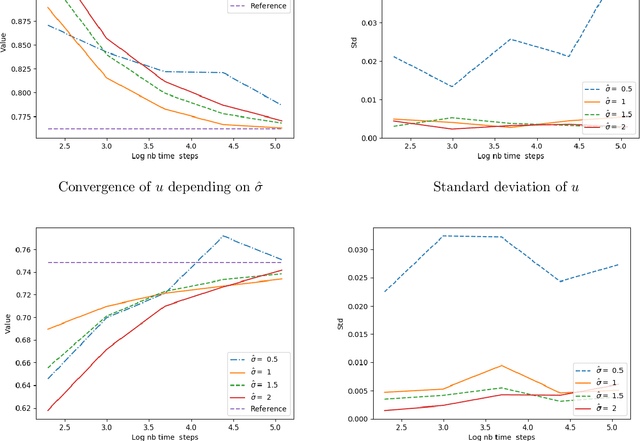
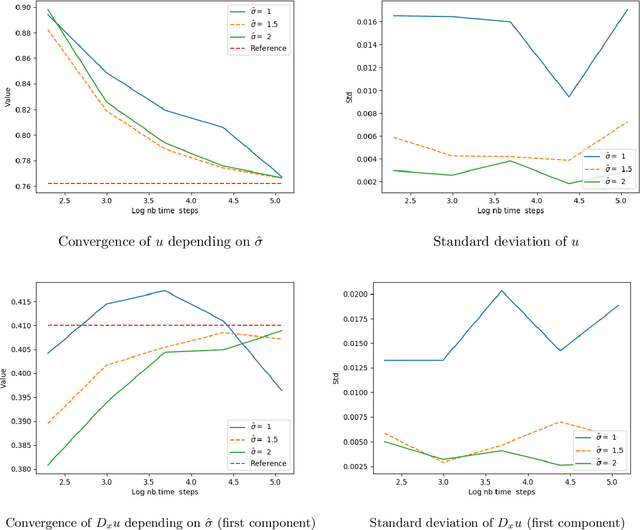
We propose a numerical method for solving high dimensional fully nonlinear partial differential equations (PDEs). Our algorithm estimates simultaneously by backward time induction the solution and its gradient by multi-layer neural networks, through a sequence of learning problems obtained from the minimization of suitable quadratic loss functions and training simulations. This methodology extends to the fully non-linear case the approach recently proposed in [HPW19] for semi-linear PDEs. Numerical tests illustrate the performance and accuracy of our method on several examples in high dimension with nonlinearity on the Hessian term including a linear quadratic control problem with control on the diffusion coefficient.