Optimization Over Trained Neural Networks: Taking a Relaxing Walk

Besides training, mathematical optimization is also used in deep learning to model and solve formulations over trained neural networks for purposes such as verification, compression, and optimization with learned constraints. However, solving these formulations soon becomes difficult as the network size grows due to the weak linear relaxation and dense constraint matrix. We have seen improvements in recent years with cutting plane algorithms, reformulations, and an heuristic based on Mixed-Integer Linear Programming (MILP). In this work, we propose a more scalable heuristic based on exploring global and local linear relaxations of the neural network model. Our heuristic is competitive with a state-of-the-art MILP solver and the prior heuristic while producing better solutions with increases in input, depth, and number of neurons.

Computational Tradeoffs of Optimization-Based Bound Tightening in ReLU Networks

The use of Mixed-Integer Linear Programming (MILP) models to represent neural networks with Rectified Linear Unit (ReLU) activations has become increasingly widespread in the last decade. This has enabled the use of MILP technology to test-or stress-their behavior, to adversarially improve their training, and to embed them in optimization models leveraging their predictive power. Many of these MILP models rely on activation bounds. That is, bounds on the input values of each neuron. In this work, we explore the tradeoff between the tightness of these bounds and the computational effort of solving the resulting MILP models. We provide guidelines for implementing these models based on the impact of network structure, regularization, and rounding.

When Deep Learning Meets Polyhedral Theory: A Survey

In the past decade, deep learning became the prevalent methodology for predictive modeling thanks to the remarkable accuracy of deep neural networks in tasks such as computer vision and natural language processing. Meanwhile, the structure of neural networks converged back to simpler representations based on piecewise constant and piecewise linear functions such as the Rectified Linear Unit (ReLU), which became the most commonly used type of activation function in neural networks. That made certain types of network structure $\unicode{x2014}$such as the typical fully-connected feedforward neural network$\unicode{x2014}$ amenable to analysis through polyhedral theory and to the application of methodologies such as Linear Programming (LP) and Mixed-Integer Linear Programming (MILP) for a variety of purposes. In this paper, we survey the main topics emerging from this fast-paced area of work, which bring a fresh perspective to understanding neural networks in more detail as well as to applying linear optimization techniques to train, verify, and reduce the size of such networks.

Getting Away with More Network Pruning: From Sparsity to Geometry and Linear Regions

One surprising trait of neural networks is the extent to which their connections can be pruned with little to no effect on accuracy. But when we cross a critical level of parameter sparsity, pruning any further leads to a sudden drop in accuracy. This drop plausibly reflects a loss in model complexity, which we aim to avoid. In this work, we explore how sparsity also affects the geometry of the linear regions defined by a neural network, and consequently reduces the expected maximum number of linear regions based on the architecture. We observe that pruning affects accuracy similarly to how sparsity affects the number of linear regions and our proposed bound for the maximum number. Conversely, we find out that selecting the sparsity across layers to maximize our bound very often improves accuracy in comparison to pruning as much with the same sparsity in all layers, thereby providing us guidance on where to prune.

Recall Distortion in Neural Network Pruning and the Undecayed Pruning Algorithm

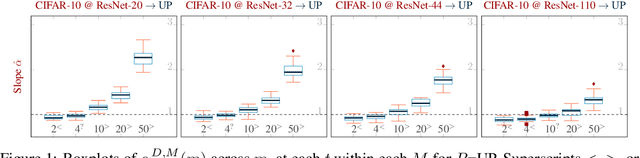
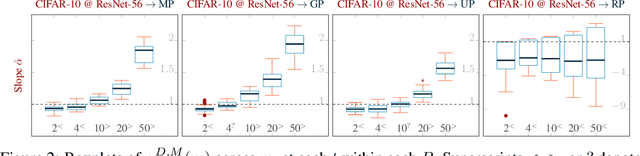
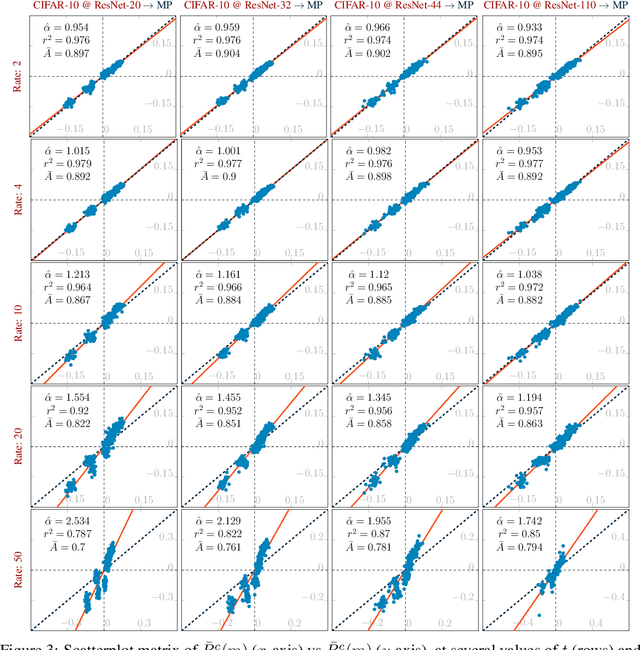
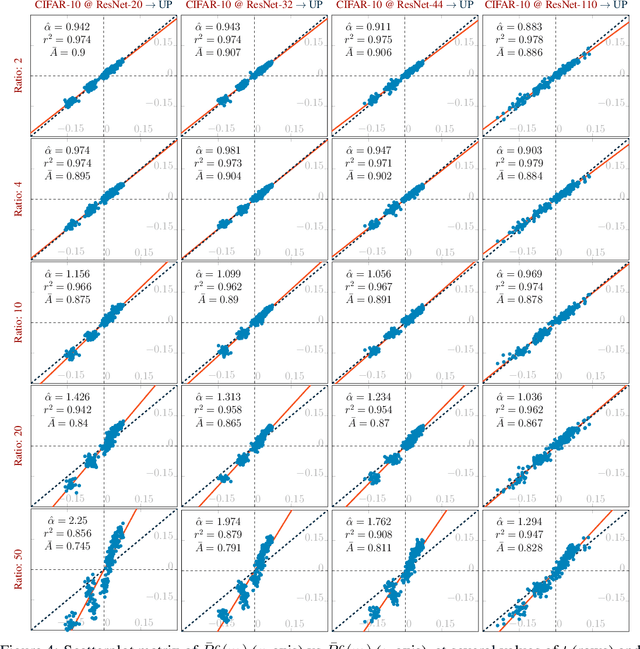
Pruning techniques have been successfully used in neural networks to trade accuracy for sparsity. However, the impact of network pruning is not uniform: prior work has shown that the recall for underrepresented classes in a dataset may be more negatively affected. In this work, we study such relative distortions in recall by hypothesizing an intensification effect that is inherent to the model. Namely, that pruning makes recall relatively worse for a class with recall below accuracy and, conversely, that it makes recall relatively better for a class with recall above accuracy. In addition, we propose a new pruning algorithm aimed at attenuating such effect. Through statistical analysis, we have observed that intensification is less severe with our algorithm but nevertheless more pronounced with relatively more difficult tasks, less complex models, and higher pruning ratios. More surprisingly, we conversely observe a de-intensification effect with lower pruning ratios.

Optimal Decision Diagrams for Classification

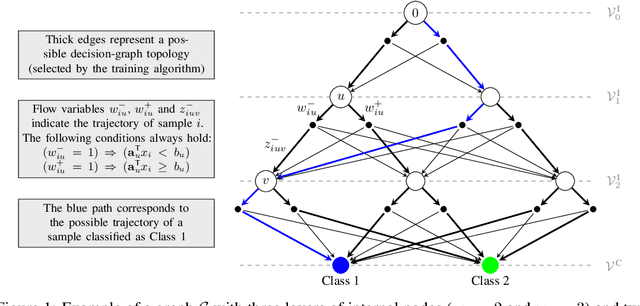
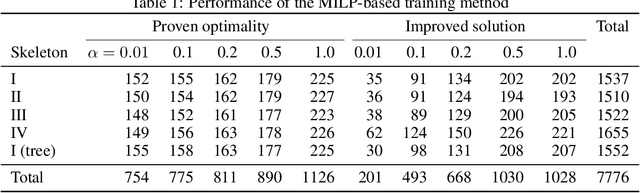
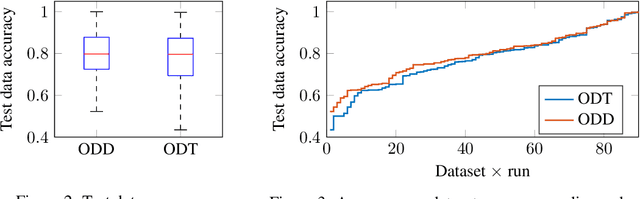
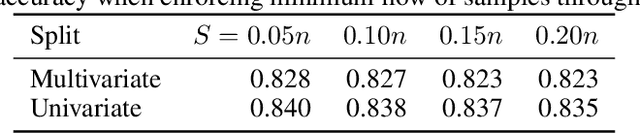
Decision diagrams for classification have some notable advantages over decision trees, as their internal connections can be determined at training time and their width is not bound to grow exponentially with their depth. Accordingly, decision diagrams are usually less prone to data fragmentation in internal nodes. However, the inherent complexity of training these classifiers acted as a long-standing barrier to their widespread adoption. In this context, we study the training of optimal decision diagrams (ODDs) from a mathematical programming perspective. We introduce a novel mixed-integer linear programming model for training and demonstrate its applicability for many datasets of practical importance. Further, we show how this model can be easily extended for fairness, parsimony, and stability notions. We present numerical analyses showing that our model allows training ODDs in short computational times, and that ODDs achieve better accuracy than optimal decision trees, while allowing for improved stability without significant accuracy losses.

The Combinatorial Brain Surgeon: Pruning Weights That Cancel One Another in Neural Networks

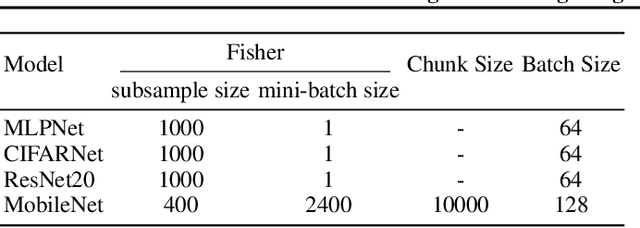
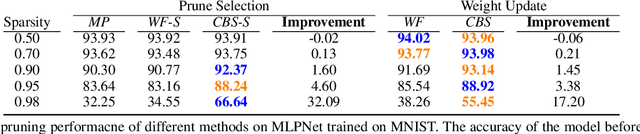
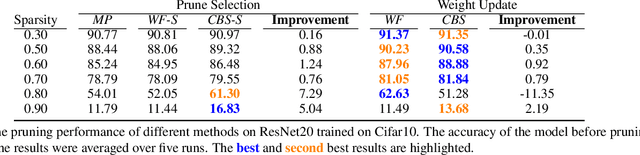
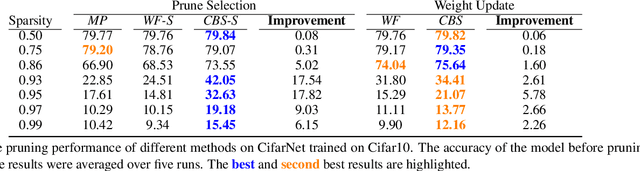
Neural networks tend to achieve better accuracy with training if they are larger -- even if the resulting models are overparameterized. Nevertheless, carefully removing such excess parameters before, during, or after training may also produce models with similar or even improved accuracy. In many cases, that can be curiously achieved by heuristics as simple as removing a percentage of the weights with the smallest absolute value -- even though magnitude is not a perfect proxy for weight relevance. With the premise that obtaining significantly better performance from pruning depends on accounting for the combined effect of removing multiple weights, we revisit one of the classic approaches for impact-based pruning: the Optimal Brain Surgeon(OBS). We propose a tractable heuristic for solving the combinatorial extension of OBS, in which we select weights for simultaneous removal, as well as a systematic update of the remaining weights. Our selection method outperforms other methods under high sparsity, and the weight update is advantageous even when combined with the other methods.

Training Thinner and Deeper Neural Networks: Jumpstart Regularization

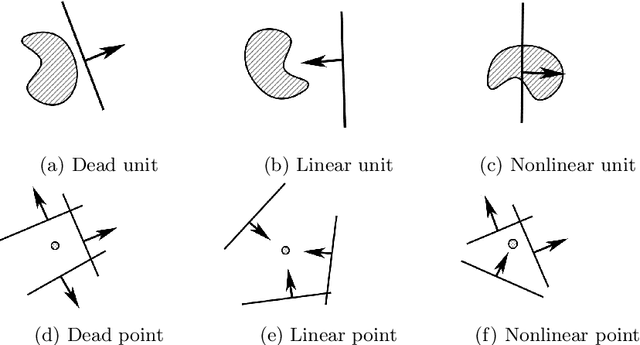
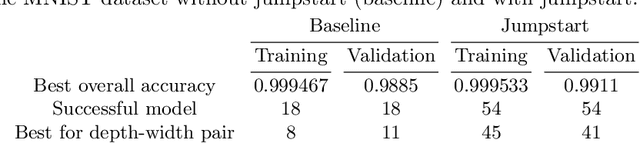
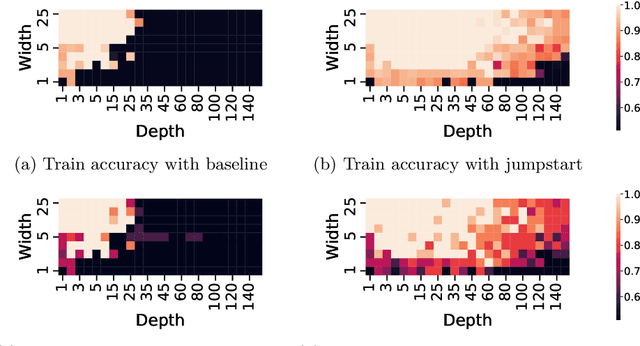
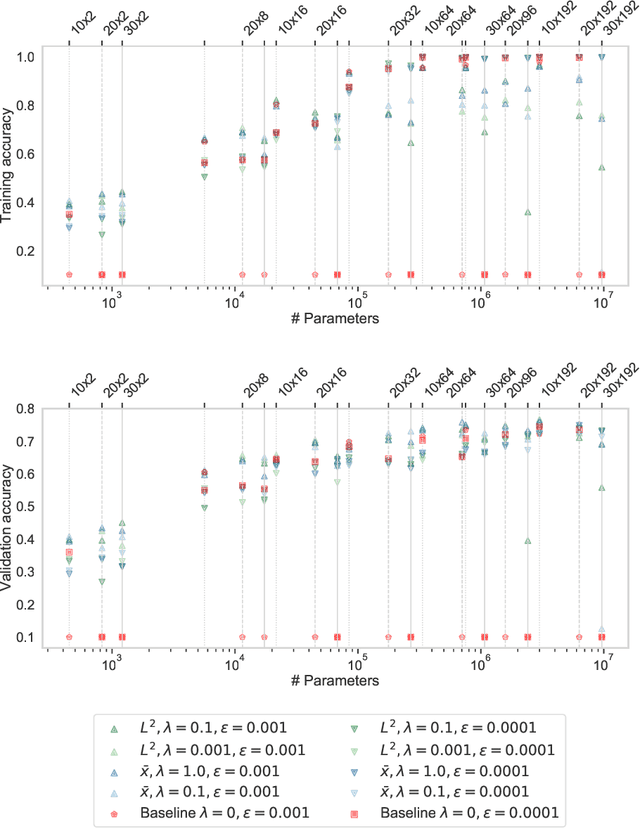
Neural networks are more expressive when they have multiple layers. In turn, conventional training methods are only successful if the depth does not lead to numerical issues such as exploding or vanishing gradients, which occur less frequently when the layers are sufficiently wide. However, increasing width to attain greater depth entails the use of heavier computational resources and leads to overparameterized models. These subsequent issues have been partially addressed by model compression methods such as quantization and pruning, some of which relying on normalization-based regularization of the loss function to make the effect of most parameters negligible. In this work, we propose instead to use regularization for preventing neurons from dying or becoming linear, a technique which we denote as jumpstart regularization. In comparison to conventional training, we obtain neural networks that are thinner, deeper, and - most importantly - more parameter-efficient.

Scaling Up Exact Neural Network Compression by ReLU Stability

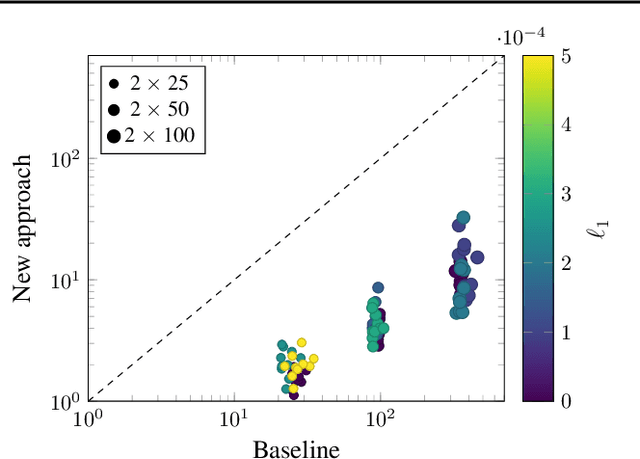
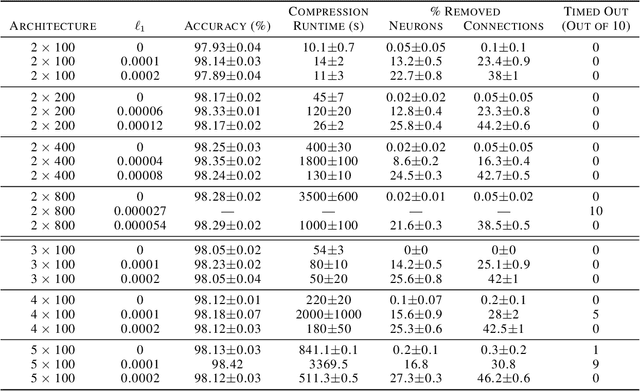
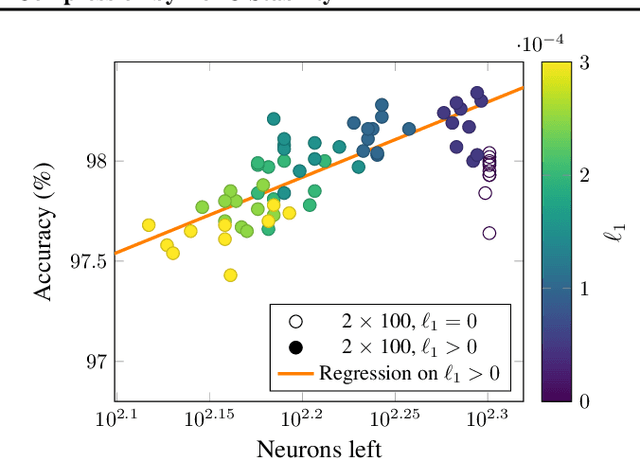
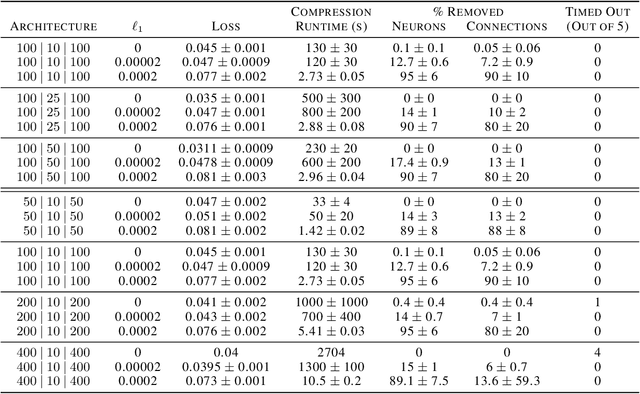
We can compress a neural network while exactly preserving its underlying functionality with respect to a given input domain if some of its neurons are stable. However, current approaches to determine the stability of neurons in networks with Rectified Linear Unit (ReLU) activations require solving or finding a good approximation to multiple discrete optimization problems. In this work, we introduce an algorithm based on solving a single optimization problem to identify all stable neurons. Our approach is on median 21 times faster than the state-of-art method, which allows us to explore exact compression on deeper (5 x 100) and wider (2 x 800) networks within minutes. For classifiers trained under an amount of L1 regularization that does not worsen accuracy, we can remove up to 40% of the connections.