Tighter sparse variational Gaussian processes

Sparse variational Gaussian process (GP) approximations based on inducing points have become the de facto standard for scaling GPs to large datasets, owing to their theoretical elegance, computational efficiency, and ease of implementation. This paper introduces a provably tighter variational approximation by relaxing the standard assumption that the conditional approximate posterior given the inducing points must match that in the prior. The key innovation is to modify the conditional posterior to have smaller variances than that of the prior at the training points. We derive the collapsed bound for the regression case, describe how to use the proposed approximation in large data settings, and discuss its application to handle orthogonally structured inducing points and GP latent variable models. Extensive experiments on regression benchmarks, classification, and latent variable models demonstrate that the proposed approximation consistently matches or outperforms standard sparse variational GPs while maintaining the same computational cost. An implementation will be made available in all popular GP packages.

Improving Uncertainty Quantification in Large Language Models via Semantic Embeddings

Accurately quantifying uncertainty in large language models (LLMs) is crucial for their reliable deployment, especially in high-stakes applications. Current state-of-the-art methods for measuring semantic uncertainty in LLMs rely on strict bidirectional entailment criteria between multiple generated responses and also depend on sequence likelihoods. While effective, these approaches often overestimate uncertainty due to their sensitivity to minor wording differences, additional correct information, and non-important words in the sequence. We propose a novel approach that leverages semantic embeddings to achieve smoother and more robust estimation of semantic uncertainty in LLMs. By capturing semantic similarities without depending on sequence likelihoods, our method inherently reduces any biases introduced by irrelevant words in the answers. Furthermore, we introduce an amortised version of our approach by explicitly modelling semantics as latent variables in a joint probabilistic model. This allows for uncertainty estimation in the embedding space with a single forward pass, significantly reducing computational overhead compared to existing multi-pass methods. Experiments across multiple question-answering datasets and frontier LLMs demonstrate that our embedding-based methods provide more accurate and nuanced uncertainty quantification than traditional approaches.

Likelihood approximations via Gaussian approximate inference

Non-Gaussian likelihoods are essential for modelling complex real-world observations but pose significant computational challenges in learning and inference. Even with Gaussian priors, non-Gaussian likelihoods often lead to analytically intractable posteriors, necessitating approximation methods. To this end, we propose efficient schemes to approximate the effects of non-Gaussian likelihoods by Gaussian densities based on variational inference and moment matching in transformed bases. These enable efficient inference strategies originally designed for models with a Gaussian likelihood to be deployed. Our empirical results demonstrate that the proposed matching strategies attain good approximation quality for binary and multiclass classification in large-scale point-estimate and distributional inferential settings. In challenging streaming problems, the proposed methods outperform all existing likelihood approximations and approximate inference methods in the exact models. As a by-product, we show that the proposed approximate log-likelihoods are a superior alternative to least-squares on raw labels for neural network classification.

Partitioned Variational Inference: A Framework for Probabilistic Federated Learning

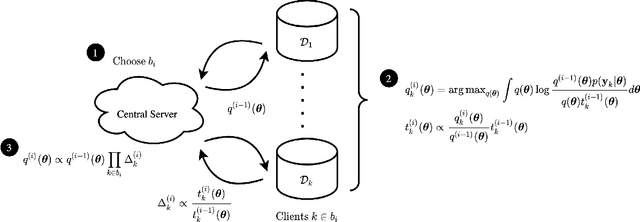
The proliferation of computing devices has brought about an opportunity to deploy machine learning models on new problem domains using previously inaccessible data. Traditional algorithms for training such models often require data to be stored on a single machine with compute performed by a single node, making them unsuitable for decentralised training on multiple devices. This deficiency has motivated the development of federated learning algorithms, which allow multiple data owners to train collaboratively and use a shared model whilst keeping local data private. However, many of these algorithms focus on obtaining point estimates of model parameters, rather than probabilistic estimates capable of capturing model uncertainty, which is essential in many applications. Variational inference (VI) has become the method of choice for fitting many modern probabilistic models. In this paper we introduce partitioned variational inference (PVI), a general framework for performing VI in the federated setting. We develop new supporting theory for PVI, demonstrating a number of properties that make it an attractive choice for practitioners; use PVI to unify a wealth of fragmented, yet related literature; and provide empirical results that showcase the effectiveness of PVI in a variety of federated settings.

Variational Auto-Regressive Gaussian Processes for Continual Learning

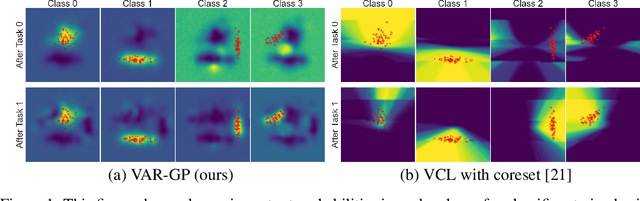
This paper proposes Variational Auto-Regressive Gaussian Process (VAR-GP), a principled Bayesian updating mechanism to incorporate new data for sequential tasks in the context of continual learning. It relies on a novel auto-regressive characterization of the variational distribution and inference is made scalable using sparse inducing point approximations. Experiments on standard continual learning benchmarks demonstrate the ability of VAR-GPs to perform well at new tasks without compromising performance on old ones, yielding competitive results to state-of-the-art methods. In addition, we qualitatively show how VAR-GP improves the predictive entropy estimates as we train on new tasks. Further, we conduct a thorough ablation study to verify the effectiveness of inferential choices.

Hierarchical Gaussian Process Priors for Bayesian Neural Network Weights

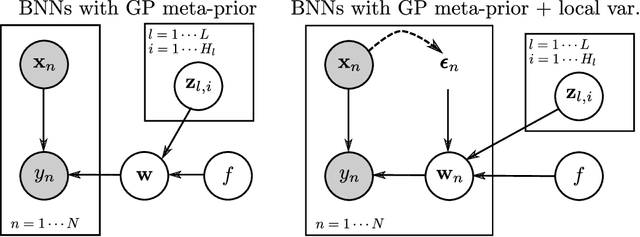
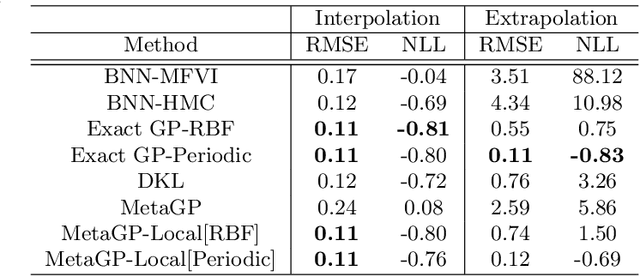
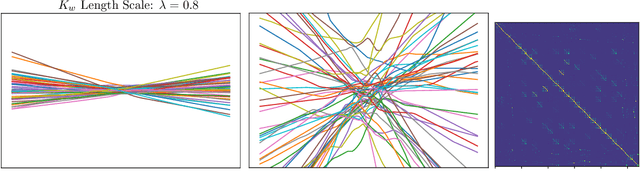
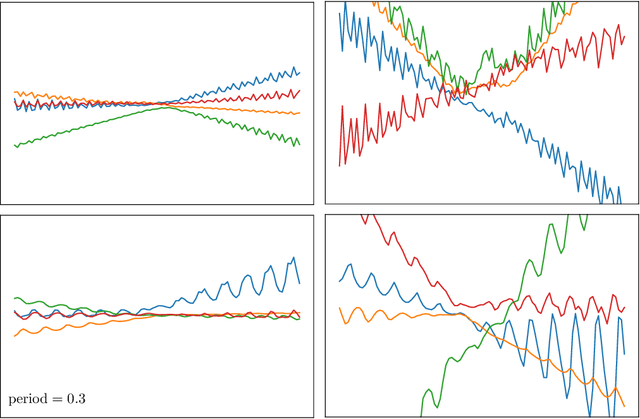
Probabilistic neural networks are typically modeled with independent weight priors, which do not capture weight correlations in the prior and do not provide a parsimonious interface to express properties in function space. A desirable class of priors would represent weights compactly, capture correlations between weights, facilitate calibrated reasoning about uncertainty, and allow inclusion of prior knowledge about the function space such as periodicity or dependence on contexts such as inputs. To this end, this paper introduces two innovations: (i) a Gaussian process-based hierarchical model for network weights based on unit embeddings that can flexibly encode correlated weight structures, and (ii) input-dependent versions of these weight priors that can provide convenient ways to regularize the function space through the use of kernels defined on contextual inputs. We show these models provide desirable test-time uncertainty estimates on out-of-distribution data, demonstrate cases of modeling inductive biases for neural networks with kernels which help both interpolation and extrapolation from training data, and demonstrate competitive predictive performance on an active learning benchmark.

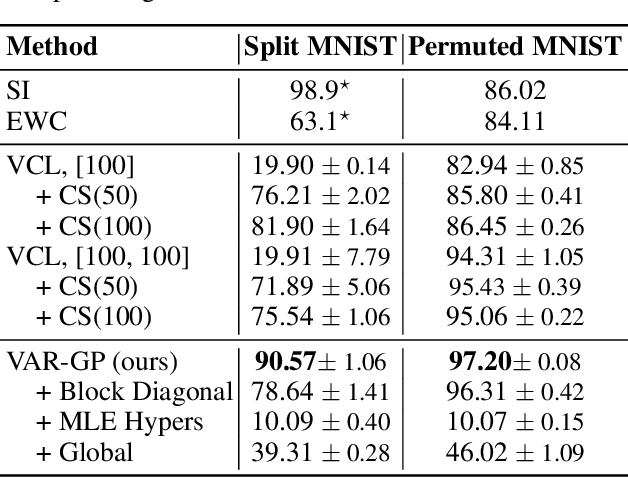
Improving and Understanding Variational Continual Learning

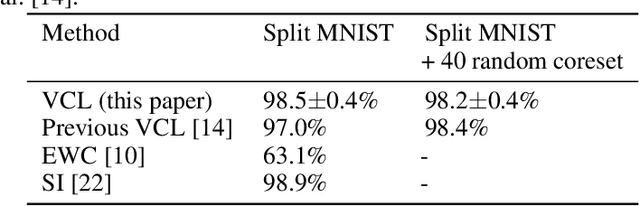
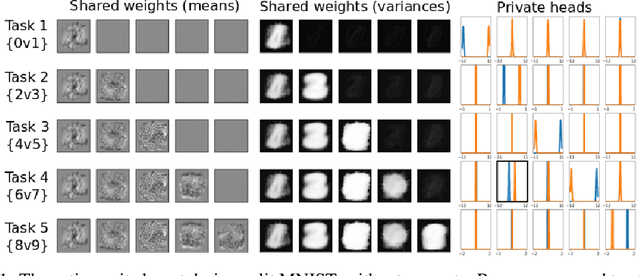
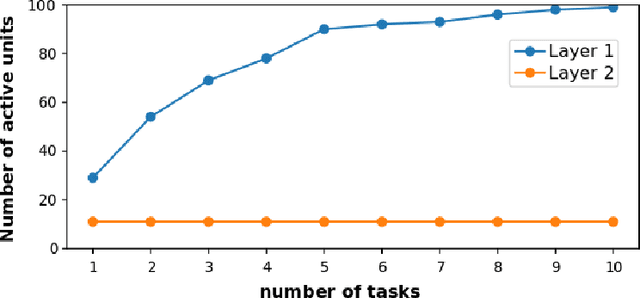
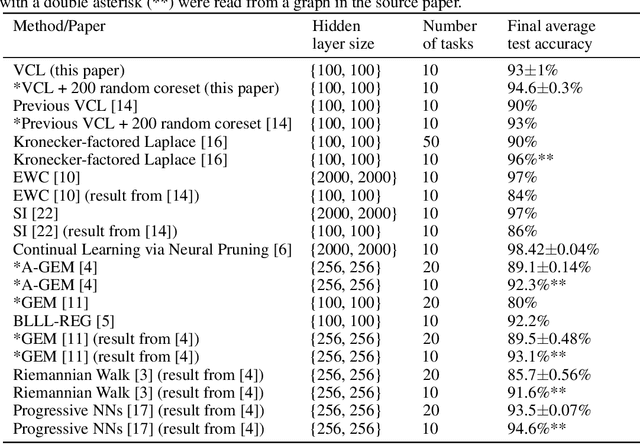
In the continual learning setting, tasks are encountered sequentially. The goal is to learn whilst i) avoiding catastrophic forgetting, ii) efficiently using model capacity, and iii) employing forward and backward transfer learning. In this paper, we explore how the Variational Continual Learning (VCL) framework achieves these desiderata on two benchmarks in continual learning: split MNIST and permuted MNIST. We first report significantly improved results on what was already a competitive approach. The improvements are achieved by establishing a new best practice approach to mean-field variational Bayesian neural networks. We then look at the solutions in detail. This allows us to obtain an understanding of why VCL performs as it does, and we compare the solution to what an `ideal' continual learning solution might be.

Partitioned Variational Inference: A unified framework encompassing federated and continual learning

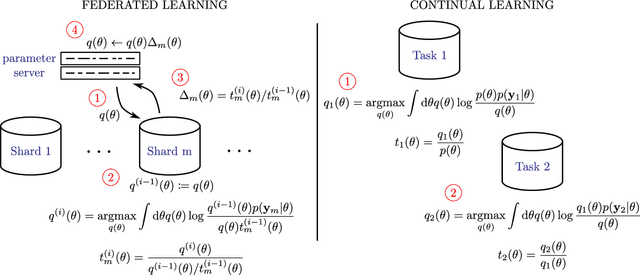
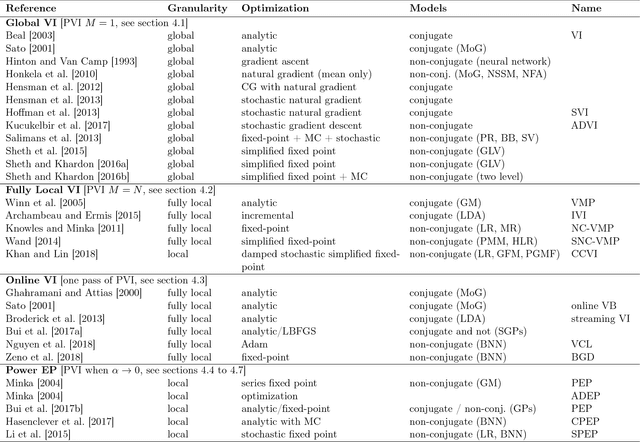
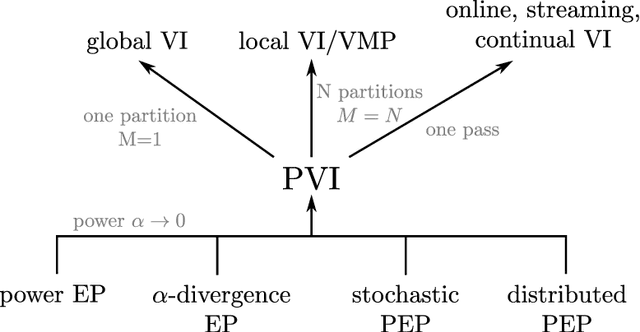
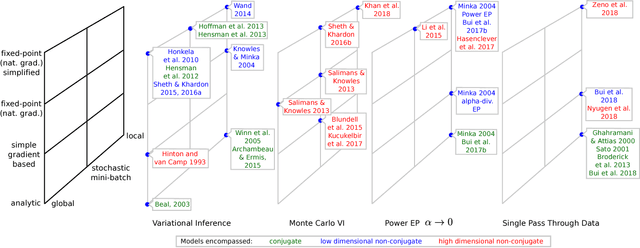
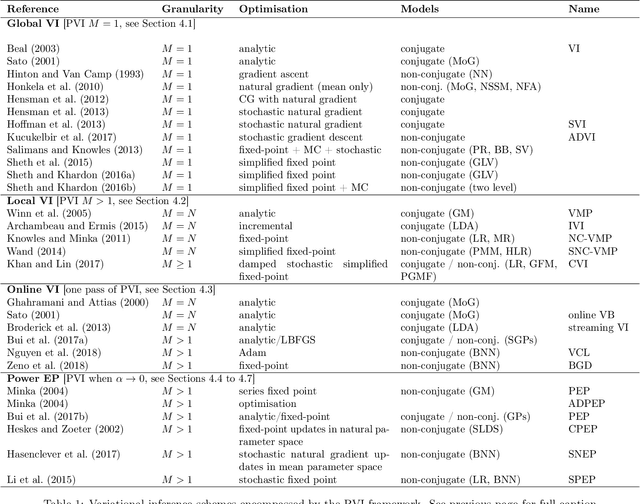
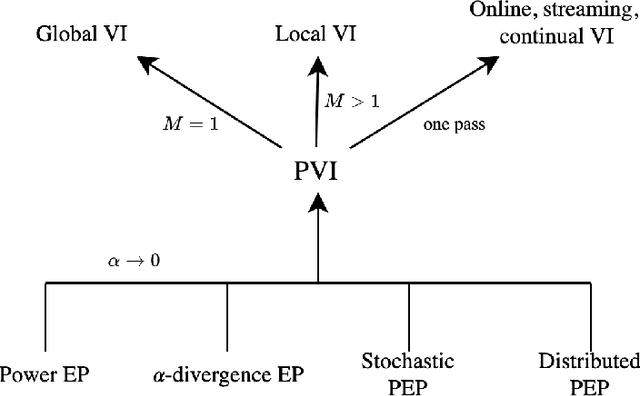
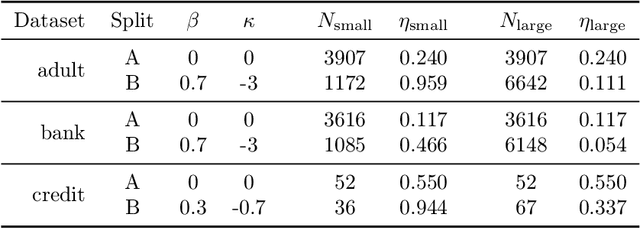
Variational inference (VI) has become the method of choice for fitting many modern probabilistic models. However, practitioners are faced with a fragmented literature that offers a bewildering array of algorithmic options. First, the variational family. Second, the granularity of the updates e.g. whether the updates are local to each data point and employ message passing or global. Third, the method of optimization (bespoke or blackbox, closed-form or stochastic updates, etc.). This paper presents a new framework, termed Partitioned Variational Inference (PVI), that explicitly acknowledges these algorithmic dimensions of VI, unifies disparate literature, and provides guidance on usage. Crucially, the proposed PVI framework allows us to identify new ways of performing VI that are ideally suited to challenging learning scenarios including federated learning (where distributed computing is leveraged to process non-centralized data) and continual learning (where new data and tasks arrive over time and must be accommodated quickly). We showcase these new capabilities by developing communication-efficient federated training of Bayesian neural networks and continual learning for Gaussian process models with private pseudo-points. The new methods significantly outperform the state-of-the-art, whilst being almost as straightforward to implement as standard VI.

Variational Continual Learning

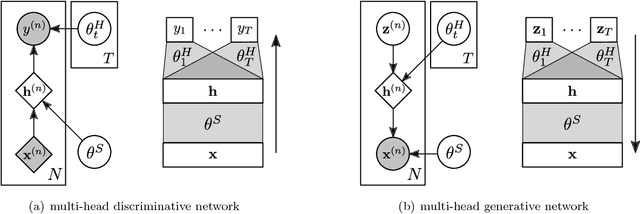
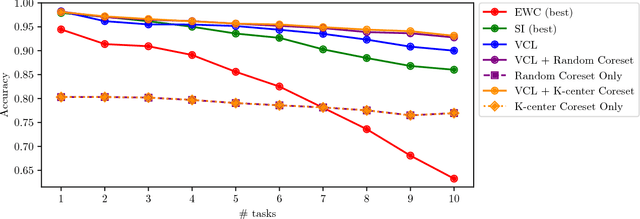
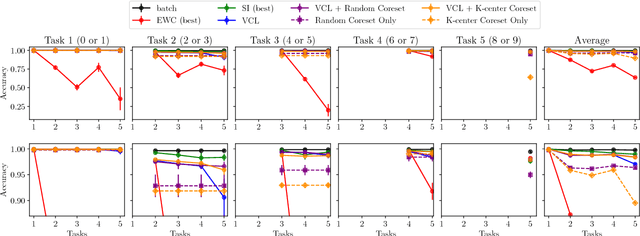
This paper develops variational continual learning (VCL), a simple but general framework for continual learning that fuses online variational inference (VI) and recent advances in Monte Carlo VI for neural networks. The framework can successfully train both deep discriminative models and deep generative models in complex continual learning settings where existing tasks evolve over time and entirely new tasks emerge. Experimental results show that VCL outperforms state-of-the-art continual learning methods on a variety of tasks, avoiding catastrophic forgetting in a fully automatic way.

Streaming Sparse Gaussian Process Approximations

Sparse pseudo-point approximations for Gaussian process (GP) models provide a suite of methods that support deployment of GPs in the large data regime and enable analytic intractabilities to be sidestepped. However, the field lacks a principled method to handle streaming data in which both the posterior distribution over function values and the hyperparameter estimates are updated in an online fashion. The small number of existing approaches either use suboptimal hand-crafted heuristics for hyperparameter learning, or suffer from catastrophic forgetting or slow updating when new data arrive. This paper develops a new principled framework for deploying Gaussian process probabilistic models in the streaming setting, providing methods for learning hyperparameters and optimising pseudo-input locations. The proposed framework is assessed using synthetic and real-world datasets.