Conditional Density Estimation Tools in Python and R with Applications to Photometric Redshifts and Likelihood-Free Cosmological Inference

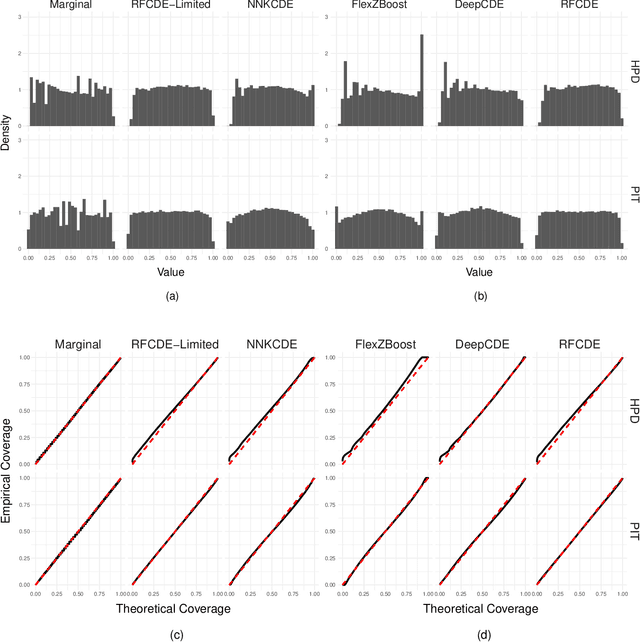
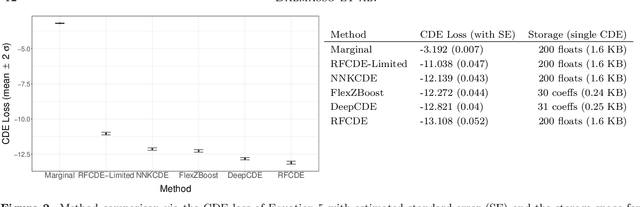
It is well known in astronomy that propagating non-Gaussian prediction uncertainty in photometric redshift estimates is key to reducing bias in downstream cosmological analyses. Similarly, likelihood-free inference approaches, which are beginning to emerge as a tool for cosmological analysis, require the full uncertainty landscape of the parameters of interest given observed data. However, most machine learning (ML) based methods with open-source software target point prediction or classification, and hence fall short in quantifying uncertainty in complex regression and parameter inference settings such as the applications mentioned above. As an alternative to methods that focus on predicting the response (or parameters) $\mathbf{y}$ from features $\mathbf{x}$, we provide nonparametric conditional density estimation (CDE) tools for approximating and validating the entire probability density $\mathrm{p}(\mathbf{y} \mid \mathbf{x})$ given training data for $\mathbf{x}$ and $\mathbf{y}$. As there is no one-size-fits-all CDE method, the goal of this work is to provide a comprehensive range of statistical tools and open-source software for nonparametric CDE and method assessment which can accommodate different types of settings and which in addition can easily be fit to the problem at hand. Specifically, we introduce CDE software packages in $\texttt{Python}$ and $\texttt{R}$ based on four ML prediction methods adapted and optimized for CDE: $\texttt{NNKCDE}$, $\texttt{RFCDE}$, $\texttt{FlexCode}$, and $\texttt{DeepCDE}$. Furthermore, we present the $\texttt{cdetools}$ package, which includes functions for computing a CDE loss function for model selection and tuning of parameters, together with diagnostics functions. We provide sample code in $\texttt{Python}$ and $\texttt{R}$ as well as examples of applications to photometric redshift estimation and likelihood-free cosmology via CDE.

Validation of Approximate Likelihood and Emulator Models for Computationally Intensive Simulations

Complex phenomena are often modeled with computationally intensive feed-forward simulations for which a tractable analytic likelihood does not exist. In these cases, it is sometimes necessary to use an approximate likelihood or faster emulator model for efficient statistical inference. We describe a new two-sample testing framework for quantifying the quality of the fit to simulations at fixed parameter values. This framework can leverage any regression method to handle complex high-dimensional data and attain higher power in settings where well-known distance-based tests would not. We also introduce a statistically rigorous test for assessing global goodness-of-fit across simulation parameters. In cases where the fit is inadequate, our method provides valuable diagnostics by allowing one to identify regions in both feature and parameter space which the model fails to reproduce well. We provide both theoretical results and examples which illustrate the effectiveness of our approach.

ABC-CDE: Towards Approximate Bayesian Computation with Complex High-Dimensional Data and Limited Simulations

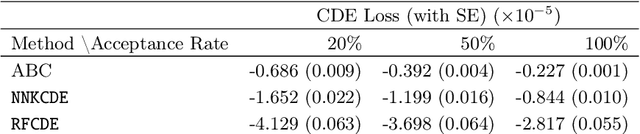
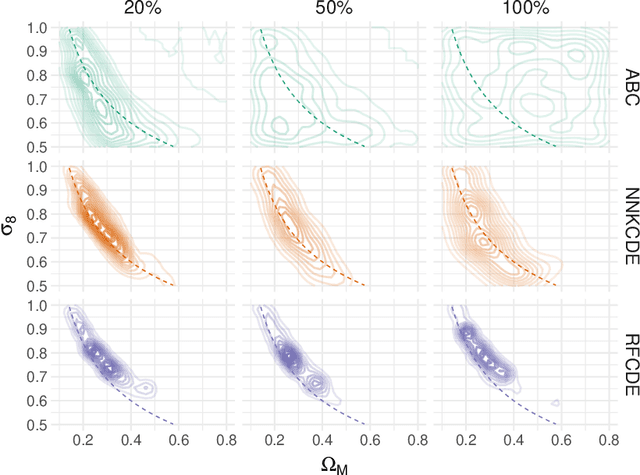
Approximate Bayesian Computation (ABC) is typically used when the likelihood is either unavailable or intractable but where data can be simulated under different parameter settings using a forward model. Despite the recent interest in ABC, high-dimensional data and costly simulations still remain a bottleneck in some applications. There is also no consensus as to how to best assess the performance of such methods without knowing the true posterior. We show how a nonparametric conditional density estimation (CDE) framework, which we refer to as ABC-CDE, help address three nontrivial challenges in ABC: (i) how to efficiently estimate the posterior distribution with limited simulations and different types of data, (ii) how to tune and compare the performance of ABC and related methods in estimating the posterior itself, rather than just certain properties of the density, and (iii) how to efficiently choose among a large set of summary statistics based on a CDE surrogate loss. We provide theoretical and empirical evidence that justify ABC-CDE procedures that {\em directly} estimate and assess the posterior based on an initial ABC sample, and we describe settings where standard ABC and regression-based approaches are inadequate.

RFCDE: Random Forests for Conditional Density Estimation

Random forests is a common non-parametric regression technique which performs well for mixed-type data and irrelevant covariates, while being robust to monotonic variable transformations. Existing random forest implementations target regression or classification. We introduce the RFCDE package for fitting random forest models optimized for nonparametric conditional density estimation, including joint densities for multiple responses. This enables analysis of conditional probability distributions which is useful for propagating uncertainty and of joint distributions that describe relationships between multiple responses and covariates. RFCDE is released under the MIT open-source license and can be accessed at https://github.com/tpospisi/rfcde . Both R and Python versions, which call a common C++ library, are available.