Reinforcement Learning with Depreciating Assets

A basic assumption of traditional reinforcement learning is that the value of a reward does not change once it is received by an agent. The present work forgoes this assumption and considers the situation where the value of a reward decays proportionally to the time elapsed since it was obtained. Emphasizing the inflection point occurring at the time of payment, we use the term asset to refer to a reward that is currently in the possession of an agent. Adopting this language, we initiate the study of depreciating assets within the framework of infinite-horizon quantitative optimization. In particular, we propose a notion of asset depreciation, inspired by classical exponential discounting, where the value of an asset is scaled by a fixed discount factor at each time step after it is obtained by the agent. We formulate a Bellman-style equational characterization of optimality in this context and develop a model-free reinforcement learning approach to obtain optimal policies.

Learning Probabilistic Reward Machines from Non-Markovian Stochastic Reward Processes

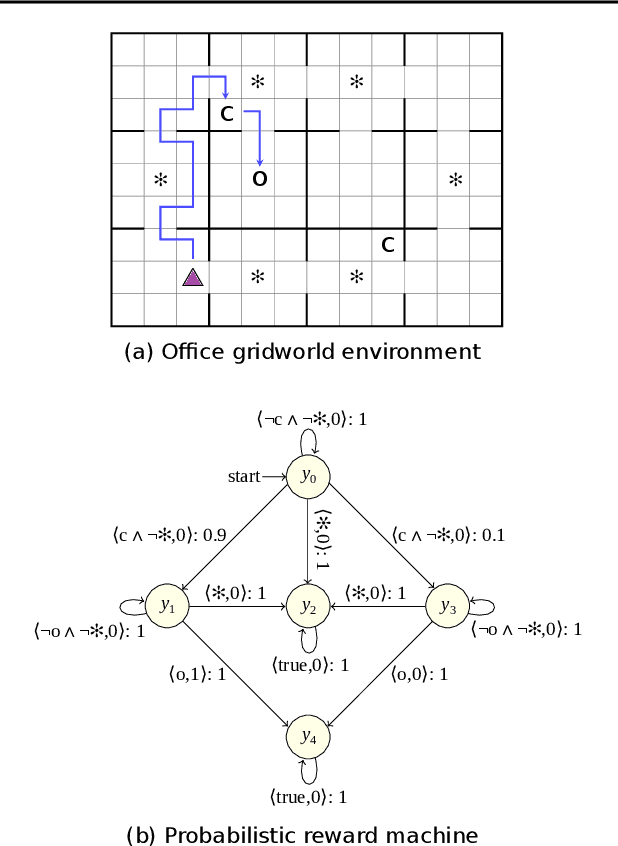
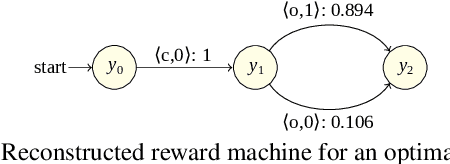
The success of reinforcement learning in typical settings is, in part, predicated on underlying Markovian assumptions on the reward signal by which an agent learns optimal policies. In recent years, the use of reward machines has relaxed this assumption by enabling a structured representation of non-Markovian rewards. In particular, such representations can be used to augment the state space of the underlying decision process, thereby facilitating non-Markovian reinforcement learning. However, these reward machines cannot capture the semantics of stochastic reward signals. In this paper, we make progress on this front by introducing probabilistic reward machines (PRMs) as a representation of non-Markovian stochastic rewards. We present an algorithm to learn PRMs from the underlying decision process as well as to learn the PRM representation of a given decision-making policy.