Learning Probabilistic Reward Machines from Non-Markovian Stochastic Reward Processes

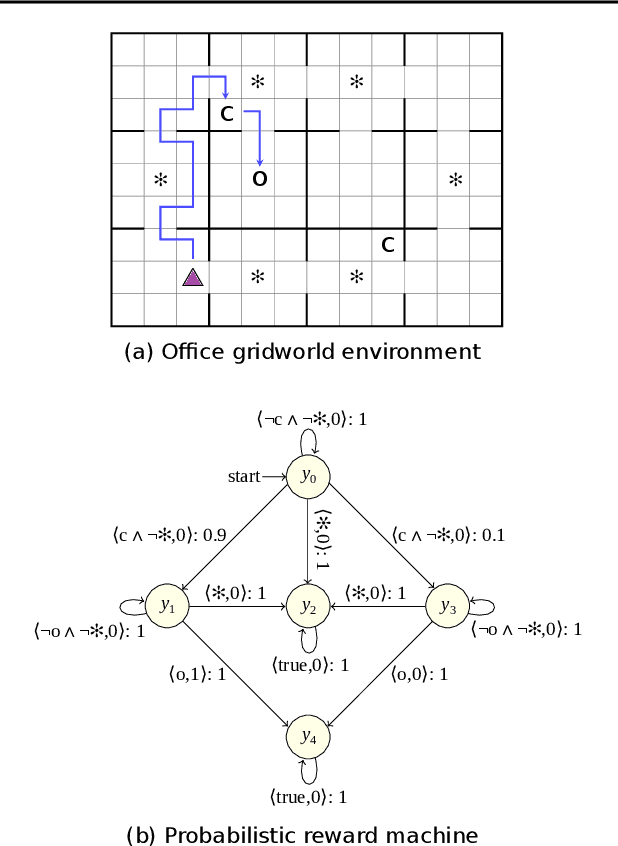
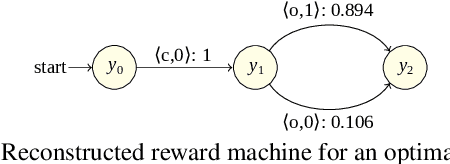
The success of reinforcement learning in typical settings is, in part, predicated on underlying Markovian assumptions on the reward signal by which an agent learns optimal policies. In recent years, the use of reward machines has relaxed this assumption by enabling a structured representation of non-Markovian rewards. In particular, such representations can be used to augment the state space of the underlying decision process, thereby facilitating non-Markovian reinforcement learning. However, these reward machines cannot capture the semantics of stochastic reward signals. In this paper, we make progress on this front by introducing probabilistic reward machines (PRMs) as a representation of non-Markovian stochastic rewards. We present an algorithm to learn PRMs from the underlying decision process as well as to learn the PRM representation of a given decision-making policy.

Functional Decision Theory in an Evolutionary Environment

Functional decision theory (FDT) is a fairly new mode of decision theory and a normative viewpoint on how an agent should maximize expected utility. The current standard in decision theory and computer science is causal decision theory (CDT), largely seen as superior to the main alternative evidential decision theory (EDT). These theories prescribe three distinct methods for maximizing utility. We explore how FDT differs from CDT and EDT, and what implications it has on the behavior of FDT agents and humans. It has been shown in previous research how FDT can outperform CDT and EDT. We additionally show FDT performing well on more classical game theory problems and argue for its extension to human problems to show that its potential for superiority is robust. We also make FDT more concrete by displaying it in an evolutionary environment, competing directly against other theories.