Evidence of Phase Transitions in Small Transformer-Based Language Models

Phase transitions have been proposed as the origin of emergent abilities in large language models (LLMs), where new capabilities appear abruptly once models surpass critical thresholds of scale. Prior work, such as that of Wei et al., demonstrated these phenomena under model and data scaling, with transitions revealed after applying a log scale to training compute. In this work, we ask three complementary questions: (1) Are phase transitions unique to large models, or can they also be observed in small transformer-based language models? (2) Can such transitions be detected directly in linear training space, rather than only after log rescaling? and (3) Can these transitions emerge at early stages of training? To investigate, we train a small GPT-style transformer on a character-level corpus and analyze the evolution of vocabulary usage throughout training. We track the average word length, the number of correct versus incorrect words, and shifts in vocabulary diversity. Building on these measures, we apply Poisson and sub-Poisson statistics to quantify how words connect and reorganize. This combined analysis reveals a distinct transition point during training. Notably, these transitions are not apparent in standard loss or validation curves, but become visible through our vocabulary- and statistics-based probes. Our findings suggest that phase-transition reorganizations are a general feature of language model training, observable even in modest models, detectable directly in linear training space, and occurring surprisingly early as coherence emerges. This perspective provides new insight into the nonlinear dynamics of language model training and underscores the importance of tailored metrics for uncovering phase transition behaviors

Convergent Complex Quasi-Newton Proximal Methods for Gradient-Driven Denoisers in Compressed Sensing MRI Reconstruction

In compressed sensing (CS) MRI, model-based methods are pivotal to achieving accurate reconstruction. One of the main challenges in model-based methods is finding an effective prior to describe the statistical distribution of the target image. Plug-and-Play (PnP) and REgularization by Denoising (RED) are two general frameworks that use denoisers as the prior. While PnP/RED methods with convolutional neural networks (CNNs) based denoisers outperform classical hand-crafted priors in CS MRI, their convergence theory relies on assumptions that do not hold for practical CNNs. The recently developed gradient-driven denoisers offer a framework that bridges the gap between practical performance and theoretical guarantees. However, the numerical solvers for the associated minimization problem remain slow for CS MRI reconstruction. This paper proposes a complex quasi-Newton proximal method that achieves faster convergence than existing approaches. To address the complex domain in CS MRI, we propose a modified Hessian estimation method that guarantees Hermitian positive definiteness. Furthermore, we provide a rigorous convergence analysis of the proposed method for nonconvex settings. Numerical experiments on both Cartesian and non-Cartesian sampling trajectories demonstrate the effectiveness and efficiency of our approach.

HOPS: High-order Polynomials with Self-supervised Dimension Reduction for Load Forecasting

Load forecasting is a fundamental task in smart grid. Many techniques have been applied to developing load forecasting models. Due to the challenges such as the Curse of Dimensionality, overfitting, and limited computing resources, multivariate higher-order polynomial models have received limited attention in load forecasting, despite their desirable mathematical foundations and optimization properties. In this paper, we propose low rank approximation and self-supervised dimension reduction to address the aforementioned issues. To further improve computational efficiency, we also introduce a fast Conjugate Gradient based algorithm for the proposed polynomial models. Based on the ISO New England dataset used in Global Energy Forecasting Competition 2017, the proposed method high-order polynomials with self-supervised dimension reduction (HOPS) demonstrates higher forecasting accuracy over several competitive models. Additionally, experimental results indicate that our approach alleviates redundant variable construction, achieving better forecasts with fewer input variables.

On Adapting Randomized Nyström Preconditioners to Accelerate Variational Image Reconstruction

Model-based iterative reconstruction plays a key role in solving inverse problems. However, the associated minimization problems are generally large-scale, ill-posed, nonsmooth, and sometimes even nonconvex, which present challenges in designing efficient iterative solvers and often prevent their practical use. Preconditioning methods can significantly accelerate the convergence of iterative methods. In some applications, computing preconditioners on-the-fly is beneficial. Moreover, forward models in image reconstruction are typically represented as operators, and the corresponding explicit matrices are often unavailable, which brings additional challenges in designing preconditioners. Therefore, for practical use, computing and applying preconditioners should be computationally inexpensive. This paper adapts the randomized Nystr\"{o}m approximation to compute effective preconditioners that accelerate image reconstruction without requiring an explicit matrix for the forward model. We leverage modern GPU computational platforms to compute the preconditioner on-the-fly. Moreover, we propose efficient approaches for applying the preconditioner to problems with nonsmooth regularizers. Our numerical results on image deblurring, super-resolution with impulsive noise, and computed tomography reconstruction demonstrate the efficiency and effectiveness of the proposed preconditioner.

Provable Preconditioned Plug-and-Play Approach for Compressed Sensing MRI Reconstruction

Model-based methods play a key role in the reconstruction of compressed sensing (CS) MRI. Finding an effective prior to describe the statistical distribution of the image family of interest is crucial for model-based methods. Plug-and-play (PnP) is a general framework that uses denoising algorithms as the prior or regularizer. Recent work showed that PnP methods with denoisers based on pretrained convolutional neural networks outperform other classical regularizers in CS MRI reconstruction. However, the numerical solvers for PnP can be slow for CS MRI reconstruction. This paper proposes a preconditioned PnP (P^2nP) method to accelerate the convergence speed. Moreover, we provide proofs of the fixed-point convergence of the P^2nP iterates. Numerical experiments on CS MRI reconstruction with non-Cartesian sampling trajectories illustrate the effectiveness and efficiency of the P^2nP approach.

A Mini-Batch Quasi-Newton Proximal Method for Constrained Total-Variation Nonlinear Image Reconstruction

Over the years, computational imaging with accurate nonlinear physical models has drawn considerable interest due to its ability to achieve high-quality reconstructions. However, such nonlinear models are computationally demanding. A popular choice for solving the corresponding inverse problems is accelerated stochastic proximal methods (ASPMs), with the caveat that each iteration is expensive. To overcome this issue, we propose a mini-batch quasi-Newton proximal method (BQNPM) tailored to image-reconstruction problems with total-variation regularization. It involves an efficient approach that computes a weighted proximal mapping at a cost similar to that of the proximal mapping in ASPMs. However, BQNPM requires fewer iterations than ASPMs to converge. We assess the performance of BQNPM on three-dimensional inverse-scattering problems with linear and nonlinear physical models. Our results on simulated and real data show the effectiveness and efficiency of BQNPM,

Coherent Wave Dynamics and Language Generation of a Generative Pre-trained Transformer

Large Language Models (LLMs), such as the Generative Pretrained Transformer (GPT), have achieved tremendous success in various language tasks, but their emergent abilities have also raised many questions, concerns, and challenges that need to be addressed. To gain a better understanding of the models' inner mechanisms, we analyze the hidden state and channel wave dynamics in a small GPT, focusing on the coherence of wave patterns in terms of cross-channel correlation and individual auto-correlation. Our findings suggest that wave dynamics offer consistent and repeatable intrinsic oscillation modes, along with context-aware plasticity and expressiveness in language generation. By analyzing wave patterns, coherence, and clustering, we provide a systematic way to identify and interpret the functionality of the hidden state channels, paving the way to understand and control higher-level language pattern formation. In addition, we investigate the Poisson statistics of spelling errors in text sequence generation across various levels of model training and observe a phase-transition-like process. As coherence builds up, there is a competition between the generation of correct and misspelled words. However, once the model is adequately trained and significant coherence has emerged, the coherent process becomes strong enough to effectively suppress spelling errors, preventing the cascade amplification of defects. The distribution of correct spellings transitions from Poissonian to Sub-Poissonian, while the distribution of misspellings shows the opposite trend. By leveraging concepts and techniques from quantum physics, we gain novel insights into the dynamics of the small GPT. This approach can be extended to larger language models that exhibit more complex coherent language patterns, opening up opportunities to interpret their emergent capabilities and develop more specialized models.

A Complex Quasi-Newton Proximal Method for Image Reconstruction in Compressed Sensing MRI

Model-based methods are widely used for reconstruction in compressed sensing (CS) magnetic resonance imaging (MRI), using priors to describe the images of interest. The reconstruction process is equivalent to solving a composite optimization problem. Accelerated proximal methods (APMs) are very popular approaches for such problems. This paper proposes a complex quasi-Newton proximal method (CQNPM) for the wavelet and total variation based CS MRI reconstruction. Compared with APMs, CQNPM requires fewer iterations to converge but needs to compute a more challenging proximal mapping called weighted proximal mapping (WPM). To make CQNPM more practical, we propose efficient methods to solve the related WPM. Numerical experiments demonstrate the effectiveness and efficiency of CQNPM.

PDO-s3DCNNs: Partial Differential Operator Based Steerable 3D CNNs

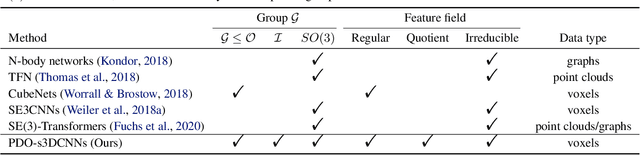
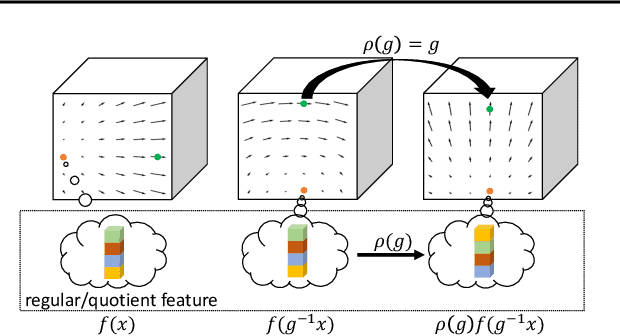
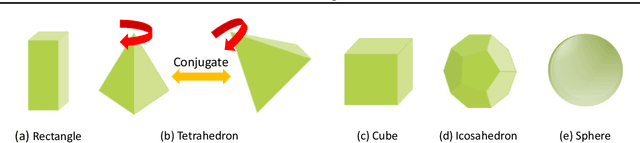
Steerable models can provide very general and flexible equivariance by formulating equivariance requirements in the language of representation theory and feature fields, which has been recognized to be effective for many vision tasks. However, deriving steerable models for 3D rotations is much more difficult than that in the 2D case, due to more complicated mathematics of 3D rotations. In this work, we employ partial differential operators (PDOs) to model 3D filters, and derive general steerable 3D CNNs, which are called PDO-s3DCNNs. We prove that the equivariant filters are subject to linear constraints, which can be solved efficiently under various conditions. As far as we know, PDO-s3DCNNs are the most general steerable CNNs for 3D rotations, in the sense that they cover all common subgroups of $SO(3)$ and their representations, while existing methods can only be applied to specific groups and representations. Extensive experiments show that our models can preserve equivariance well in the discrete domain, and outperform previous works on SHREC'17 retrieval and ISBI 2012 segmentation tasks with a low network complexity.

Diffraction Tomography with Helmholtz Equation: Efficient and Robust Multigrid-Based Solver

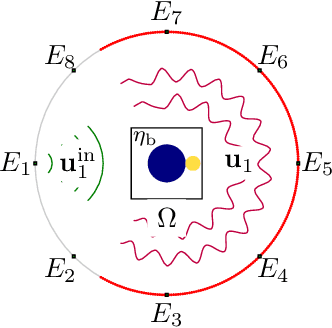
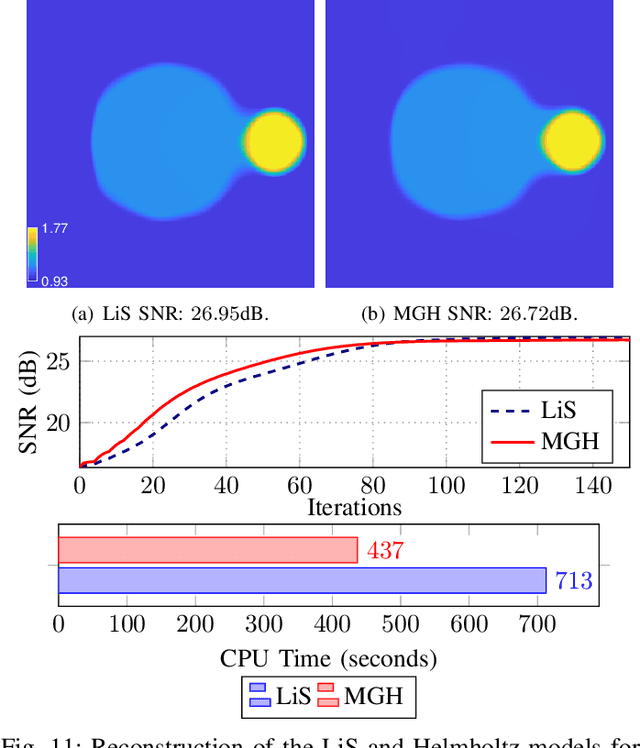
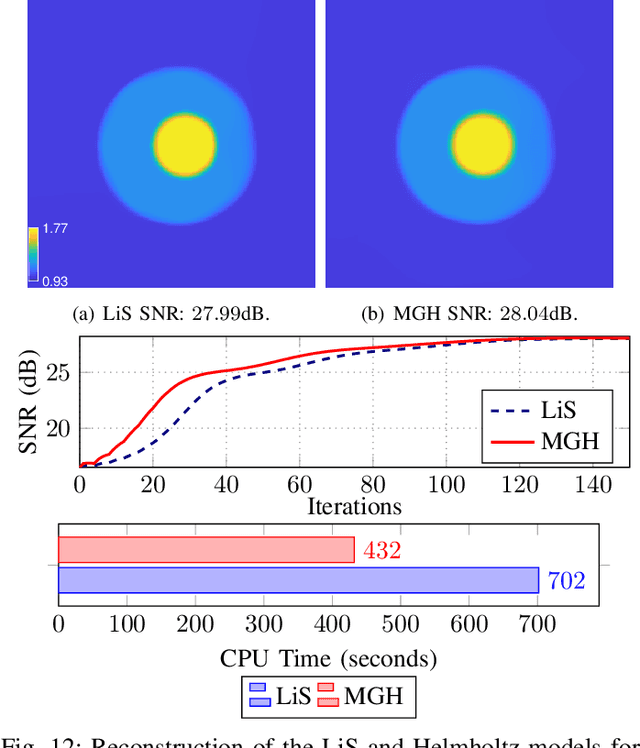
Diffraction tomography is a noninvasive technique that estimates the refractive indices of unknown objects and involves an inverse-scattering problem governed by the wave equation. Recent works have shown the benefit of nonlinear models of wave propagation that account for multiple scattering and reflections. In particular, the Lippmann-Schwinger~(LiS) model defines an inverse problem to simulate the wave propagation. Although accurate, this model is hard to solve when the samples are highly contrasted or have a large physical size. In this work, we introduce instead a Helmholtz-based nonlinear model for inverse scattering. To solve the corresponding inverse problem, we propose a robust and efficient multigrid-based solver. Moreover, we show that our method is a suitable alternative to the LiS model, especially for strongly scattering objects. Numerical experiments on simulated and real data demonstrate the effectiveness of the Helmholtz model, as well as the efficiency of the proposed multigrid method.