Subsampling Factorization Machine Annealing

Quantum computing and machine learning are state-of-the-art technologies which have been investigated intensively in both academia and industry. The hybrid technology of these two ingredients is expected to be a powerful tool to solve complex problems in many branches of science and engineering such as combinatorial optimization problems and accelerate the creation of next-generation technologies. In this work, we develop an algorithm to solve a black-box optimization problem by improving Factorization Machine Annealing (FMA) such that the training of a machine learning model called Factorization Machine is performed not by a full dataset but by a subdataset which is sampled from a full dataset: Subsampling Factorization Machine Annealing (SFMA). According to such a probabilistic training process, the performance of FMA on exploring a solution space gets enhanced. As a result, SFMA exhibits balanced performance of exploration and exploitation which we call exploitation-exploration functionality. We conduct numerical benchmarking tests to compare the performance of SFMA with that of FMA. Consequently, SFMA certainly exhibits the exploration-exploitation functionality and outperforms FMA in speed and accuracy. In addition, the performance of SFMA can be further improved by sequentially using two subsampling datasets with different sizes such that the size of the latter dataset is substantially smaller than the former. Such a substantial reduction not only enhances the exploration performance of SFMA but also enables us to run it with correspondingly low computational cost even for a large-scale problem. These results indicate the effectiveness of SFMA in a certain class of black-box optimization problems of significant size: the potential scalability of SFMA in solving large-scale problems with correspondingly low computational cost.

Quantum Computing and AI: Perspectives on Advanced Automation in Science and Engineering

Recent advances in artificial intelligence (AI) and quantum computing are accelerating automation in scientific and engineering processes, fundamentally reshaping research methodologies. This perspective highlights parallels between scientific automation and established Computer-Aided Engineering (CAE) practices, introducing Quantum CAE as a framework that leverages quantum algorithms for simulation, optimization, and machine learning within engineering design. Practical implementations of Quantum CAE are illustrated through case studies for combinatorial optimization problems. Further discussions include advancements toward higher automation levels, highlighting the critical role of specialized AI agents proficient in quantum algorithm design. The integration of quantum computing with AI raises significant questions about the collaborative dynamics among human scientists and engineers, AI systems, and quantum computational resources, underscoring a transformative future for automated discovery and innovation.

Generative quantum combinatorial optimization by means of a novel conditional generative quantum eigensolver

Quantum computing is entering a transformative phase with the emergence of logical quantum processors, which hold the potential to tackle complex problems beyond classical capabilities. While significant progress has been made, applying quantum algorithms to real-world problems remains challenging. Hybrid quantum-classical techniques have been explored to bridge this gap, but they often face limitations in expressiveness, trainability, or scalability. In this work, we introduce conditional Generative Quantum Eigensolver (conditional-GQE), a context-aware quantum circuit generator powered by an encoder-decoder Transformer. Focusing on combinatorial optimization, we train our generator for solving problems with up to 10 qubits, exhibiting nearly perfect performance on new problems. By leveraging the high expressiveness and flexibility of classical generative models, along with an efficient preference-based training scheme, conditional-GQE provides a generalizable and scalable framework for quantum circuit generation. Our approach advances hybrid quantum-classical computing and contributes to accelerate the transition toward fault-tolerant quantum computing.

Lossy compression of matrices by black-box optimisation of mixed-integer non-linear programming

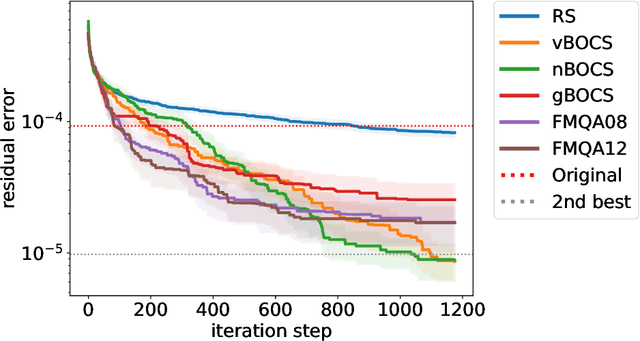
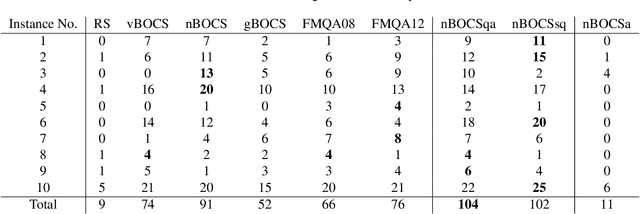
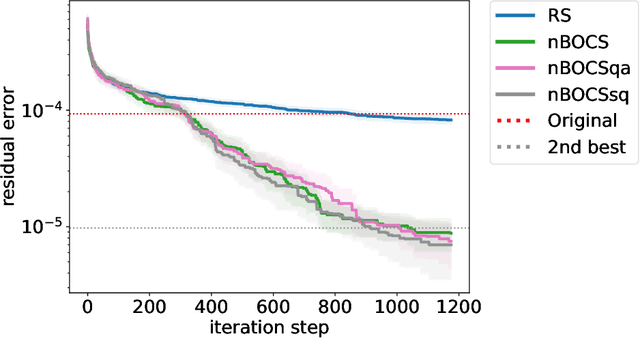
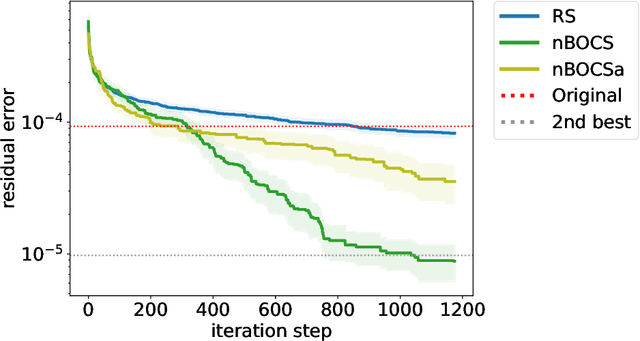
In edge computing, suppressing data size is a challenge for machine learning models that perform complex tasks such as autonomous driving, in which computational resources (speed, memory size and power) are limited. Efficient lossy compression of matrix data has been introduced by decomposing it into the product of an integer and real matrices. However, its optimisation is difficult as it requires simultaneous optimisation of an integer and real variables. In this paper, we improve this optimisation by utilising recently developed black-box optimisation (BBO) algorithms with an Ising solver for integer variables. In addition, the algorithm can be used to solve mixed-integer programming problems that are linear and non-linear in terms of real and integer variables, respectively. The differences between the choice of Ising solvers (simulated annealing (SA), quantum annealing (QA) and simulated quenching (SQ)) and the strategies of the BBO algorithms (BOCS, FMQA and their variations) are discussed for further development of the BBO techniques.

Application of QUBO solver using black-box optimization to structural design for resonance avoidance

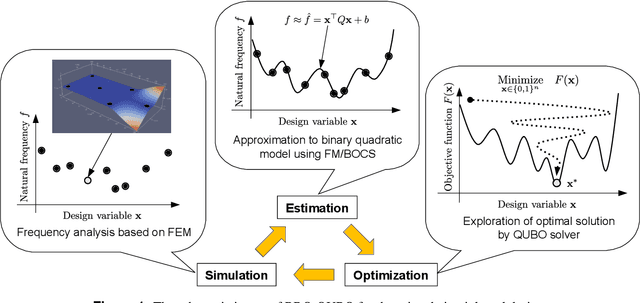
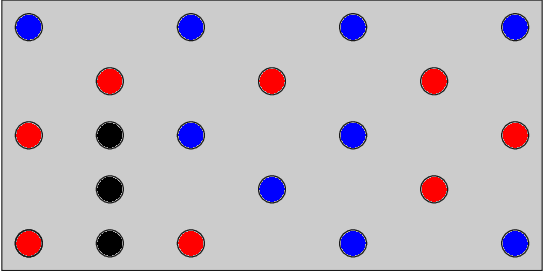
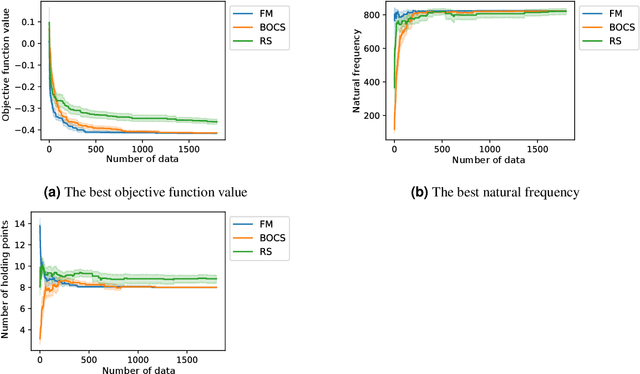
Quadratic unconstrained binary optimization (QUBO) solvers can be applied to design an optimal structure to avoid resonance. QUBO algorithms that work on a classical or quantum device have succeeded in some industrial applications. However, their applications are still limited due to the difficulty of transforming from the original optimization problem to QUBO. Recently, black-box optimization (BBO) methods have been proposed to tackle this issue using a machine learning technique and a Bayesian treatment for combinatorial optimization. We employed the BBO methods to design a printed circuit board for resonance avoidance. This design problem is formulated to maximize natural frequency and simultaneously minimize the number of mounting points. The natural frequency, which is the bottleneck for the QUBO formulation, is approximated to a quadratic model in the BBO method. We demonstrated that BBO using a factorization machine shows good performance in both the calculation time and the success probability of finding the optimal solution. Our results can open up QUBO solvers' potential for other applications in structural designs.