Reservoir Predictive Path Integral Control for Unknown Nonlinear Dynamics

Neural networks capable of approximating complex nonlinearities have found extensive application in data-driven control of nonlinear dynamical systems. However, fast online identification and control of unknown dynamics remain central challenges. This paper integrates echo-state networks (ESNs) -- reservoir computing models implemented with recurrent neural networks -- and model predictive path integral (MPPI) control -- sampling-based variants of model predictive control -- to meet these challenges. The proposed reservoir predictive path integral (RPPI) enables fast learning of nonlinear dynamics with ESN and exploits the learned nonlinearities directly in parallelized MPPI control computation without linearization approximations. The framework is further extended to uncertainty-aware RPPI (URPPI), which leverages ESN uncertainty to balance exploration and exploitation: exploratory inputs dominate during early learning, while exploitative inputs prevail as model confidence grows. Experiments on controlling the Duffing oscillator and four-tank systems demonstrate that URPPI improves control performance, reducing control costs by up to 60% compared to traditional quadratic programming-based model predictive control methods.

Application of QUBO solver using black-box optimization to structural design for resonance avoidance

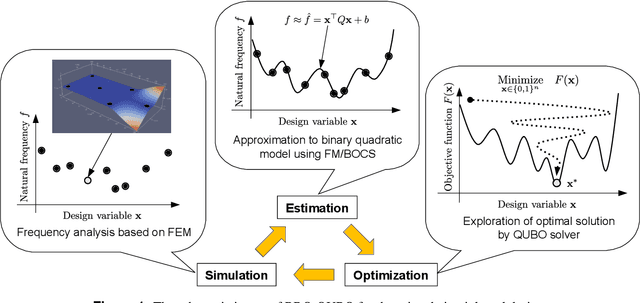
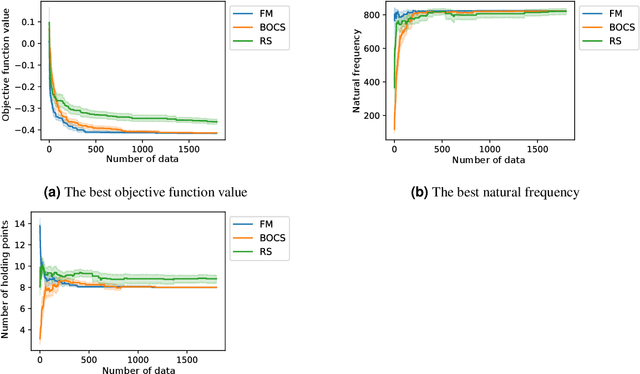
Quadratic unconstrained binary optimization (QUBO) solvers can be applied to design an optimal structure to avoid resonance. QUBO algorithms that work on a classical or quantum device have succeeded in some industrial applications. However, their applications are still limited due to the difficulty of transforming from the original optimization problem to QUBO. Recently, black-box optimization (BBO) methods have been proposed to tackle this issue using a machine learning technique and a Bayesian treatment for combinatorial optimization. We employed the BBO methods to design a printed circuit board for resonance avoidance. This design problem is formulated to maximize natural frequency and simultaneously minimize the number of mounting points. The natural frequency, which is the bottleneck for the QUBO formulation, is approximated to a quadratic model in the BBO method. We demonstrated that BBO using a factorization machine shows good performance in both the calculation time and the success probability of finding the optimal solution. Our results can open up QUBO solvers' potential for other applications in structural designs.

Reservoir Computing with Diverse Timescales for Prediction of Multiscale Dynamics

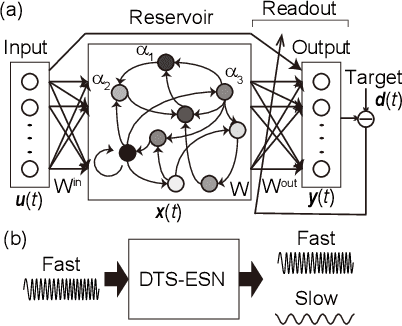
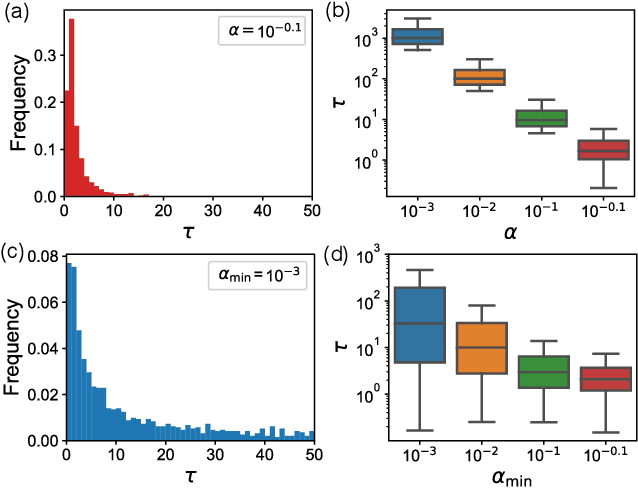
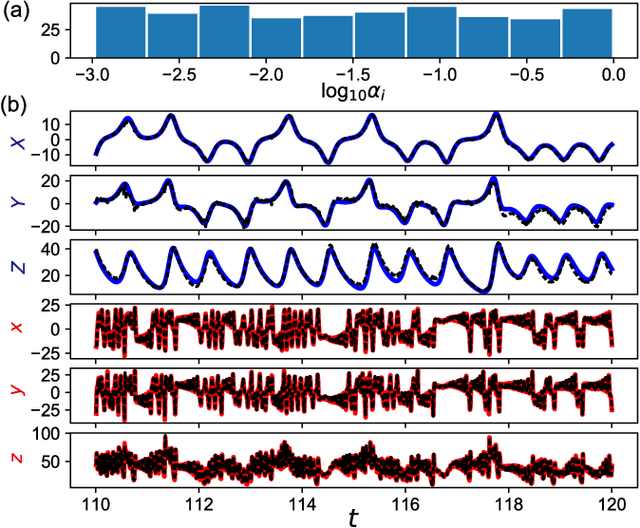
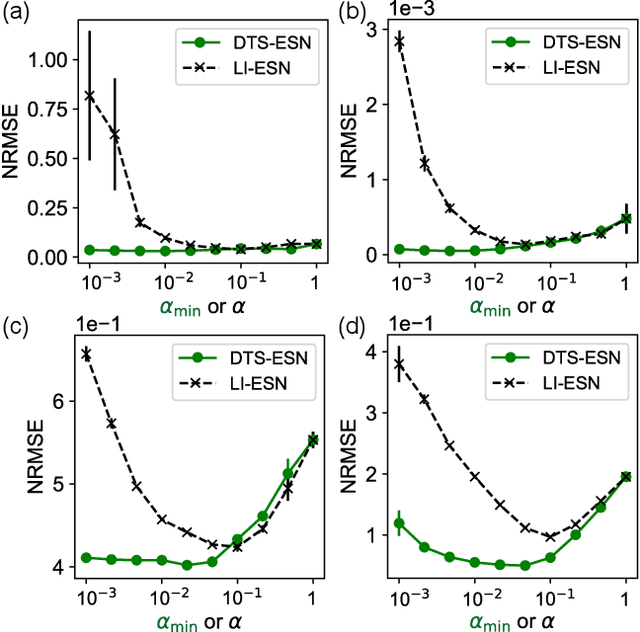
Machine learning approaches have recently been leveraged as a substitute or an aid for physical/mathematical modeling approaches to dynamical systems. To develop an efficient machine learning method dedicated to modeling and prediction of multiscale dynamics, we propose a reservoir computing model with diverse timescales by using a recurrent network of heterogeneous leaky integrator neurons. In prediction tasks with fast-slow chaotic dynamical systems including a large gap in timescales of their subsystems dynamics, we demonstrate that the proposed model has a higher potential than the existing standard model and yields a performance comparable to the best one of the standard model even without an optimization of the leak rate parameter. Our analysis reveals that the timescales required for producing each component of target dynamics are appropriately and flexibly selected from the reservoir dynamics by model training.