Susan Holmes
ASCLEPIOS
Geomstats: A Python Package for Riemannian Geometry in Machine Learning
Apr 07, 2020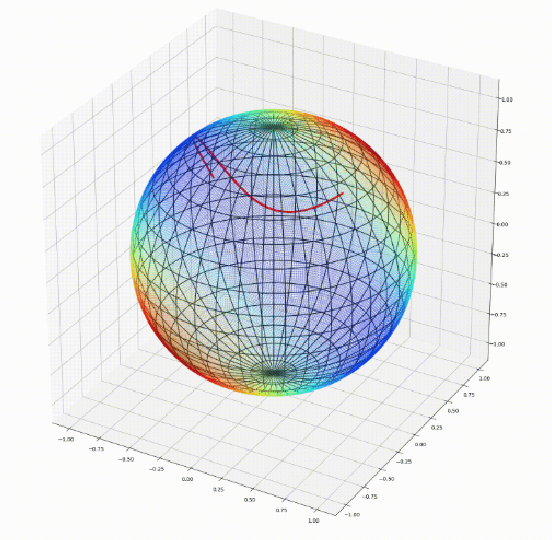

Abstract:We introduce Geomstats, an open-source Python toolbox for computations and statistics on nonlinear manifolds, such as hyperbolic spaces, spaces of symmetric positive definite matrices, Lie groups of transformations, and many more. We provide object-oriented and extensively unit-tested implementations. Among others, manifolds come equipped with families of Riemannian metrics, with associated exponential and logarithmic maps, geodesics and parallel transport. Statistics and learning algorithms provide methods for estimation, clustering and dimension reduction on manifolds. All associated operations are vectorized for batch computation and provide support for different execution backends, namely NumPy, PyTorch and TensorFlow, enabling GPU acceleration. This paper presents the package, compares it with related libraries and provides relevant code examples. We show that Geomstats provides reliable building blocks to foster research in differential geometry and statistics, and to democratize the use of Riemannian geometry in machine learning applications. The source code is freely available under the MIT license at \url{geomstats.ai}.
Convex Hierarchical Clustering for Graph-Structured Data
Dec 11, 2019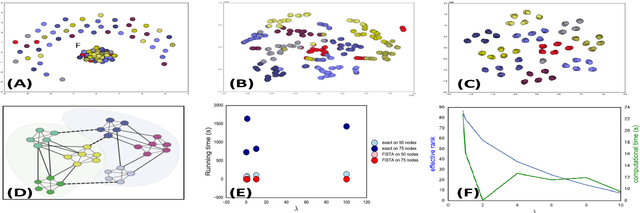
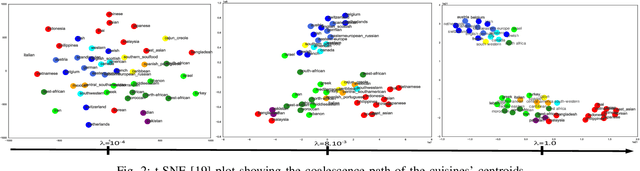
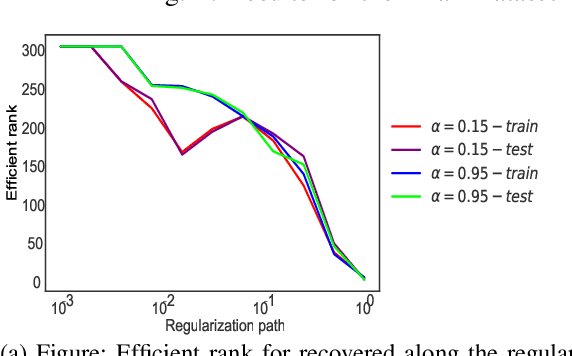
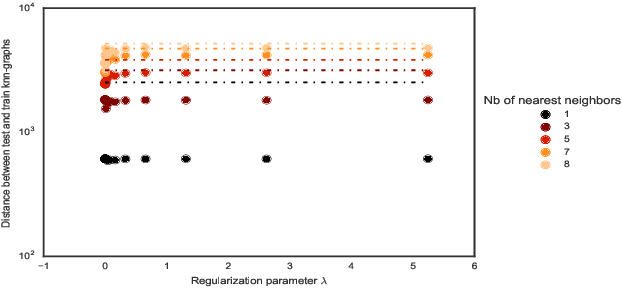
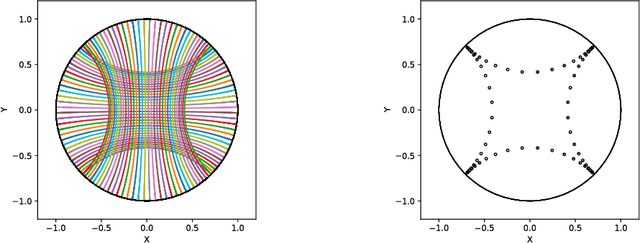
Abstract:Convex clustering is a recent stable alternative to hierarchical clustering. It formulates the recovery of progressively coalescing clusters as a regularized convex problem. While convex clustering was originally designed for handling Euclidean distances between data points, in a growing number of applications, the data is directly characterized by a similarity matrix or weighted graph. In this paper, we extend the robust hierarchical clustering approach to these broader classes of similarities. Having defined an appropriate convex objective, the crux of this adaptation lies in our ability to provide: (a) an efficient recovery of the regularization path and (b) an empirical demonstration of the use of our method. We address the first challenge through a proximal dual algorithm, for which we characterize both the theoretical efficiency as well as the empirical performance on a set of experiments. Finally, we highlight the potential of our method by showing its application to several real-life datasets, thus providing a natural extension to the current scope of applications of convex clustering.
Learning Weighted Submanifolds with Variational Autoencoders and Riemannian Variational Autoencoders
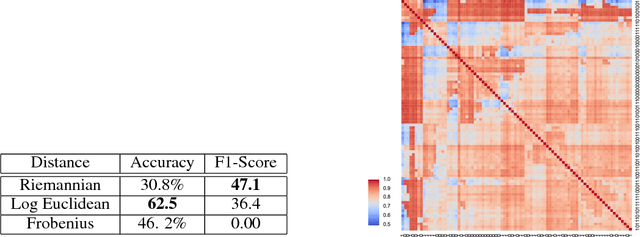
Nov 19, 2019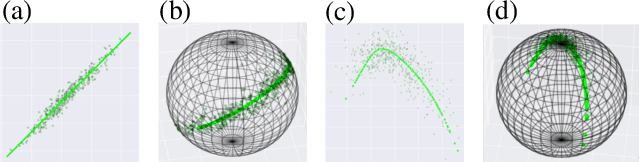
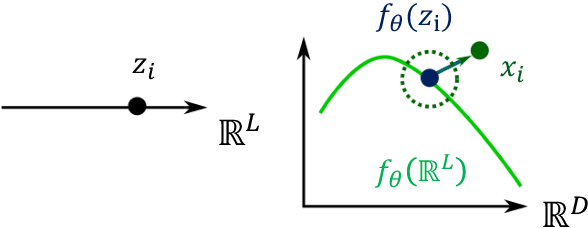
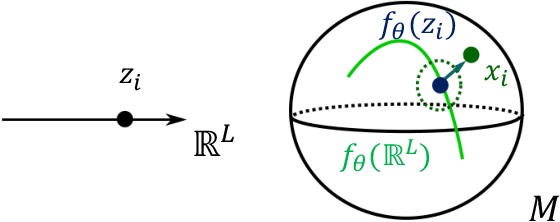
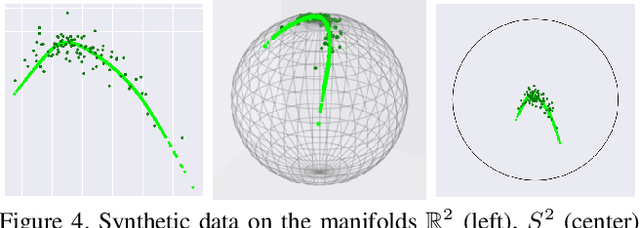
Abstract:Manifold-valued data naturally arises in medical imaging. In cognitive neuroscience, for instance, brain connectomes base the analysis of coactivation patterns between different brain regions on the analysis of the correlations of their functional Magnetic Resonance Imaging (fMRI) time series - an object thus constrained by construction to belong to the manifold of symmetric positive definite matrices. One of the challenges that naturally arises consists of finding a lower-dimensional subspace for representing such manifold-valued data. Traditional techniques, like principal component analysis, are ill-adapted to tackle non-Euclidean spaces and may fail to achieve a lower-dimensional representation of the data - thus potentially pointing to the absence of lower-dimensional representation of the data. However, these techniques are restricted in that: (i) they do not leverage the assumption that the connectomes belong on a pre-specified manifold, therefore discarding information; (ii) they can only fit a linear subspace to the data. In this paper, we are interested in variants to learn potentially highly curved submanifolds of manifold-valued data. Motivated by the brain connectomes example, we investigate a latent variable generative model, which has the added benefit of providing us with uncertainty estimates - a crucial quantity in the medical applications we are considering. While latent variable models have been proposed to learn linear and nonlinear spaces for Euclidean data, or geodesic subspaces for manifold data, no intrinsic latent variable model exists to learn nongeodesic subspaces for manifold data. This paper fills this gap and formulates a Riemannian variational autoencoder with an intrinsic generative model of manifold-valued data. We evaluate its performances on synthetic and real datasets by introducing the formalism of weighted Riemannian submanifolds.
Estimation of Orientation and Camera Parameters from Cryo-Electron Microscopy Images with Variational Autoencoders and Generative Adversarial Networks
Nov 19, 2019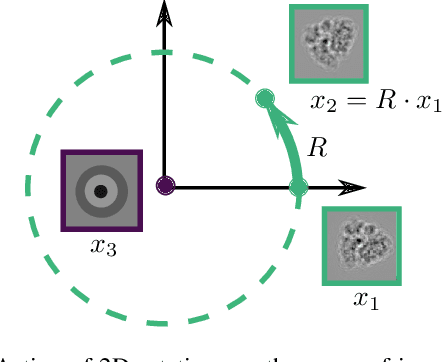
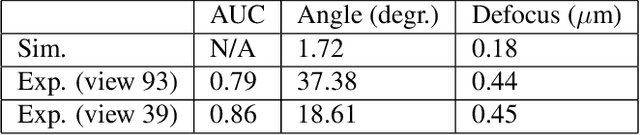
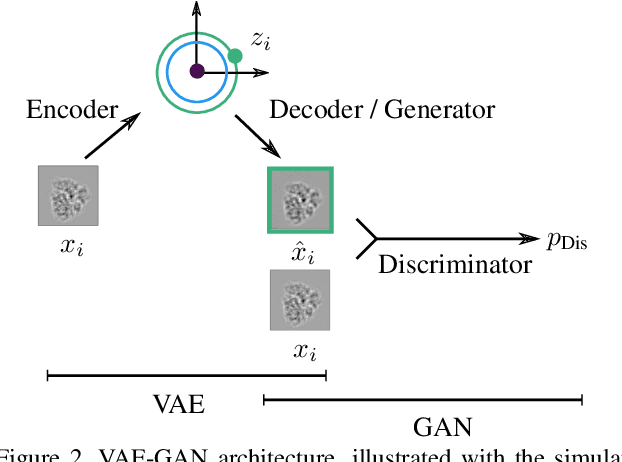

Abstract:Cryo-electron microscopy (cryo-EM) is capable of producing reconstructed 3D images of biomolecules at near-atomic resolution. As such, it represents one of the most promising imaging techniques in structural biology. However, raw cryo-EM images are only highly corrupted - noisy and band-pass filtered - 2D projections of the target 3D biomolecules. Reconstructing the 3D molecular shape starts with the removal of image outliers, the estimation of the orientation of the biomolecule that has produced the given 2D image, and the estimation of camera parameters to correct for intensity defects. Current techniques performing these tasks are often computationally expensive, while the dataset sizes keep growing. There is a need for next-generation algorithms that preserve accuracy while improving speed and scalability. In this paper, we combine variational autoencoders (VAEs) and generative adversarial networks (GANs) to learn a low-dimensional latent representation of cryo-EM images. We perform an exploratory analysis of the obtained latent space, that is shown to have a structure of "orbits", in the sense of Lie group theory, consistent with the acquisition procedure of cryo-EM images. This analysis leads us to design an estimation method for orientation and camera parameters of single-particle cryo-EM images, together with an outliers detection procedure. As such, it opens the door to geometric approaches for unsupervised estimations of orientations and camera parameters, making possible fast cryo-EM biomolecule reconstruction.
Template shape estimation: correcting an asymptotic bias
Feb 02, 2017
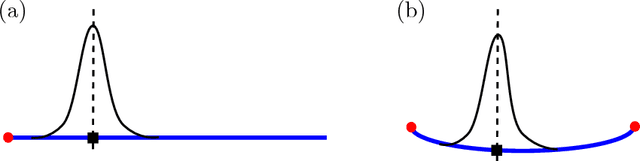
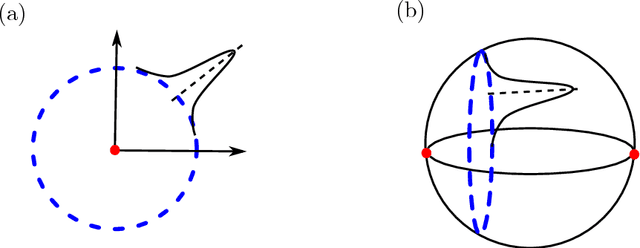
Abstract:We use tools from geometric statistics to analyze the usual estimation procedure of a template shape. This applies to shapes from landmarks, curves, surfaces, images etc. We demonstrate the asymptotic bias of the template shape estimation using the stratified geometry of the shape space. We give a Taylor expansion of the bias with respect to a parameter $\sigma$ describing the measurement error on the data. We propose two bootstrap procedures that quantify the bias and correct it, if needed. They are applicable for any type of shape data. We give a rule of thumb to provide intuition on whether the bias has to be corrected. This exhibits the parameters that control the bias' magnitude. We illustrate our results on simulated and real shape data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge