Tube Loss: A Novel Approach for Prediction Interval Estimation and probabilistic forecasting

This paper proposes a novel loss function, called 'Tube Loss', for simultaneous estimation of bounds of a Prediction Interval (PI) in the regression setup, and also for generating probabilistic forecasts from time series data solving a single optimization problem. The PIs obtained by minimizing the empirical risk based on the Tube Loss are shown to be of better quality than the PIs obtained by the existing methods in the following sense. First, it yields intervals that attain the prespecified confidence level $t \in(0,1)$ asymptotically. A theoretical proof of this fact is given. Secondly, the user is allowed to move the interval up or down by controlling the value of a parameter. This helps the user to choose a PI capturing denser regions of the probability distribution of the response variable inside the interval, and thus, sharpening its width. This is shown to be especially useful when the conditional distribution of the response variable is skewed. Further, the Tube Loss based PI estimation method can trade-off between the coverage and the average width by solving a single optimization problem. It enables further reduction of the average width of PI through re-calibration. Also, unlike a few existing PI estimation methods the gradient descent (GD) method can be used for minimization of empirical risk. Finally, through extensive experimentation, we have shown the efficacy of the Tube Loss based PI estimation in kernel machines, neural networks and deep networks and also for probabilistic forecasting tasks. The codes of the experiments are available at https://github.com/ltpritamanand/Tube_loss

Improvement over Pinball Loss Support Vector Machine

Recently, there have been several papers that discuss the extension of the Pinball loss Support Vector Machine (Pin-SVM) model, originally proposed by Huang et al.,[1][2]. Pin-SVM classifier deals with the pinball loss function, which has been defined in terms of the parameter $\tau$. The parameter $\tau$ can take values in $[ -1,1]$. The existing Pin-SVM model requires to solve the same optimization problem for all values of $\tau$ in $[ -1,1]$. In this paper, we improve the existing Pin-SVM model for the binary classification task. At first, we note that there is major difficulty in Pin-SVM model (Huang et al. [1]) for $ -1 \leq \tau < 0$. Specifically, we show that the Pin-SVM model requires the solution of different optimization problem for $ -1 \leq \tau < 0$. We further propose a unified model termed as Unified Pin-SVM which results in a QPP valid for all $-1\leq \tau \leq 1$ and hence more convenient to use. The proposed Unified Pin-SVM model can obtain a significant improvement in accuracy over the existing Pin-SVM model which has also been empirically justified by extensive numerical experiments with real-world datasets.

Twin Augmented Architectures for Robust Classification of COVID-19 Chest X-Ray Images

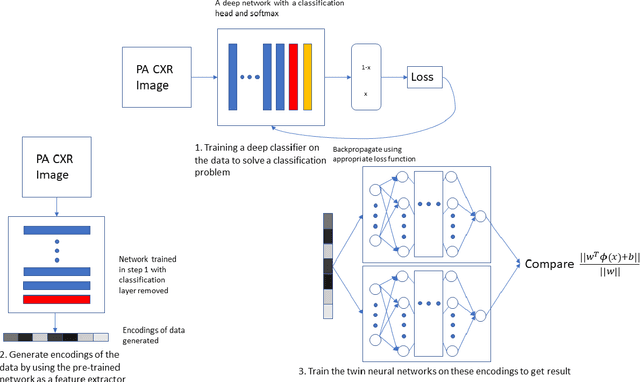
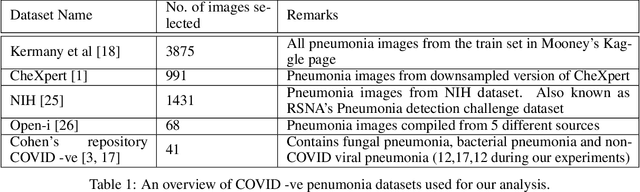
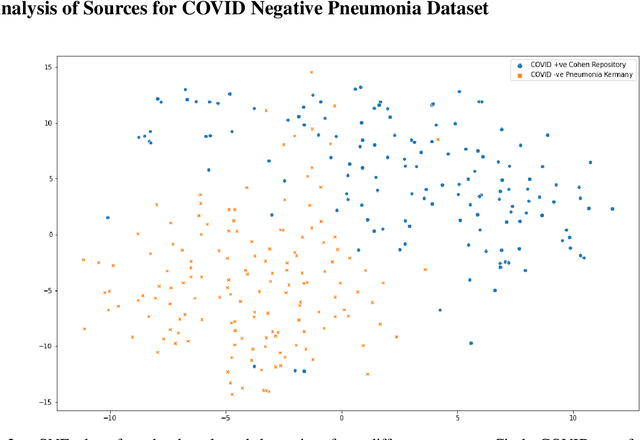
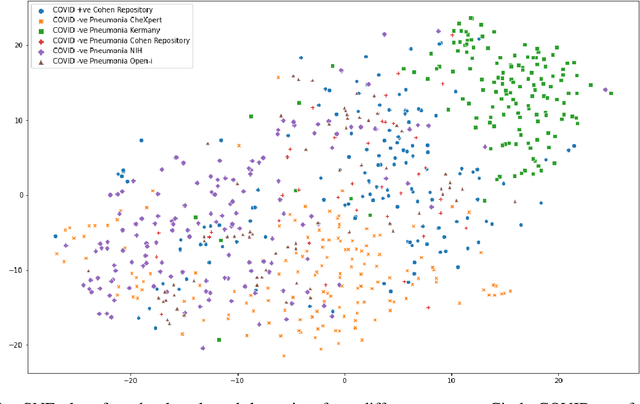
The gold standard for COVID-19 is RT-PCR, testing facilities for which are limited and not always optimally distributed. Test results are delayed, which impacts treatment. Expert radiologists, one of whom is a co-author, are able to diagnose COVID-19 positivity from Chest X-Rays (CXR) and CT scans, that can facilitate timely treatment. Such diagnosis is particularly valuable in locations lacking radiologists with sufficient expertise and familiarity with COVID-19 patients. This paper has two contributions. One, we analyse literature on CXR based COVID-19 diagnosis. We show that popular choices of dataset selection suffer from data homogeneity, leading to misleading results. We compile and analyse a viable benchmark dataset from multiple existing heterogeneous sources. Such a benchmark is important for realistically testing models. Our second contribution relates to learning from imbalanced data. Datasets for COVID X-Ray classification face severe class imbalance, since most subjects are COVID -ve. Twin Support Vector Machines (Twin SVM) and Twin Neural Networks (Twin NN) have, in recent years, emerged as effective ways of handling skewed data. We introduce a state-of-the-art technique, termed as Twin Augmentation, for modifying popular pre-trained deep learning models. Twin Augmentation boosts the performance of a pre-trained deep neural network without requiring re-training. Experiments show, that across a multitude of classifiers, Twin Augmentation is very effective in boosting the performance of given pre-trained model for classification in imbalanced settings.

A $ν$- support vector quantile regression model with automatic accuracy control

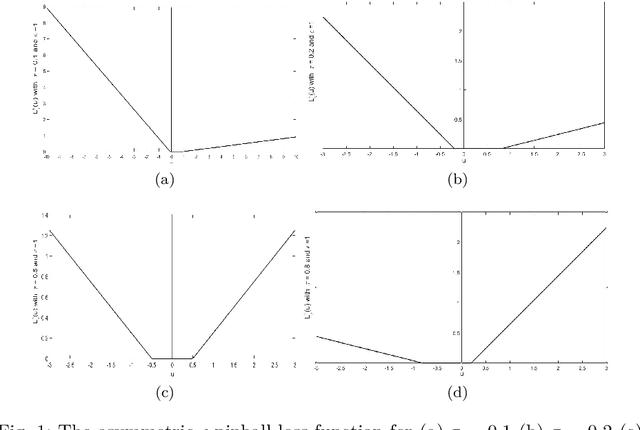
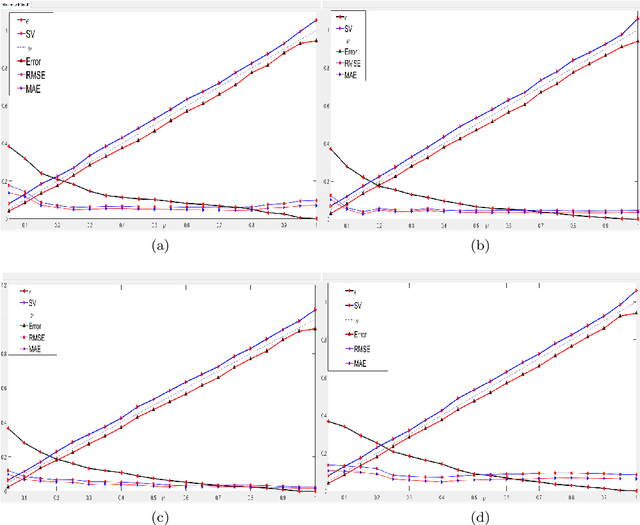
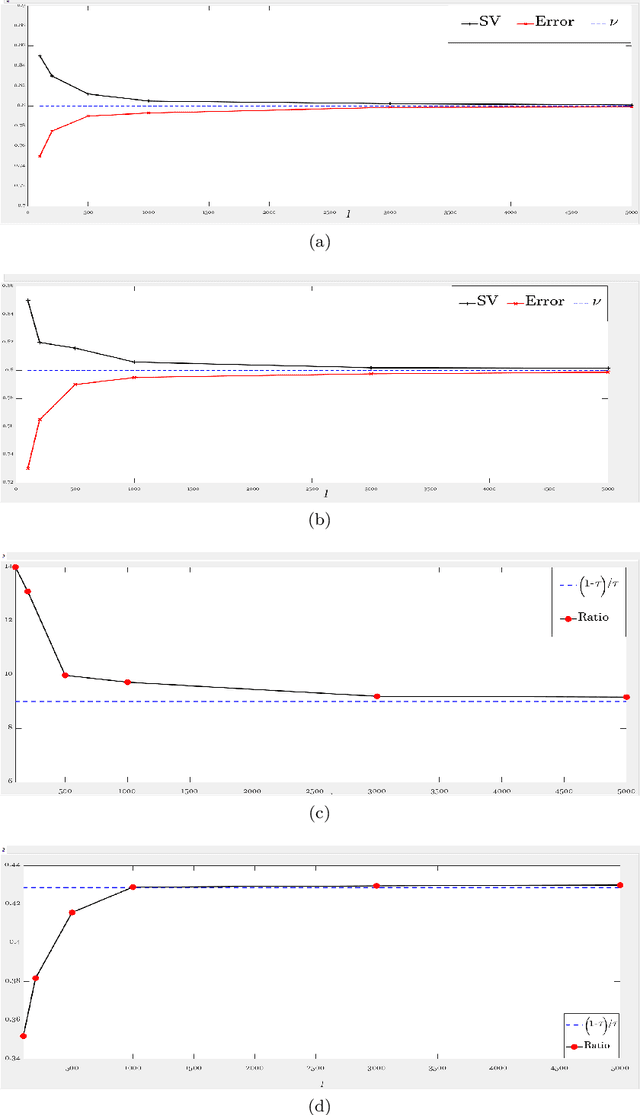
This paper proposes a novel '$\nu$-support vector quantile regression' ($\nu$-SVQR) model for the quantile estimation. It can facilitate the automatic control over accuracy by creating a suitable asymmetric $\epsilon$-insensitive zone according to the variance present in data. The proposed $\nu$-SVQR model uses the $\nu$ fraction of training data points for the estimation of the quantiles. In the $\nu$-SVQR model, training points asymptotically appear above and below of the asymmetric $\epsilon$-insensitive tube in the ratio of $1-\tau$ and $\tau$. Further, there are other interesting properties of the proposed $\nu$-SVQR model, which we have briefly described in this paper. These properties have been empirically verified using the artificial and real world dataset also.

A new asymmetric $ε$-insensitive pinball loss function based support vector quantile regression model

In this paper, we propose a novel asymmetric $\epsilon$-insensitive pinball loss function for quantile estimation. There exists some pinball loss functions which attempt to incorporate the $\epsilon$-insensitive zone approach in it but, they fail to extend the $\epsilon$-insensitive approach for quantile estimation in true sense. The proposed asymmetric $\epsilon$-insensitive pinball loss function can make an asymmetric $\epsilon$- insensitive zone of fixed width around the data and divide it using $\tau$ value for the estimation of the $\tau$th quantile. The use of the proposed asymmetric $\epsilon$-insensitive pinball loss function in Support Vector Quantile Regression (SVQR) model improves its prediction ability significantly. It also brings the sparsity back in SVQR model. Further, the numerical results obtained by several experiments carried on artificial and real world datasets empirically show the efficacy of the proposed `$\epsilon$-Support Vector Quantile Regression' ($\epsilon$-SVQR) model over other existing SVQR models.

Support Vector Regression via a Combined Reward Cum Penalty Loss Function

In this paper, we introduce a novel combined reward cum penalty loss function to handle the regression problem. The proposed combined reward cum penalty loss function penalizes the data points which lie outside the $\epsilon$-tube of the regressor and also assigns reward for the data points which lie inside of the $\epsilon$-tube of the regressor. The combined reward cum penalty loss function based regression (RP-$\epsilon$-SVR) model has several interesting properties which are investigated in this paper and are also supported with the experimental results.

Learning a hyperplane regressor by minimizing an exact bound on the VC dimension

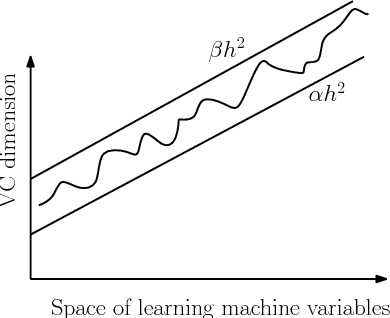
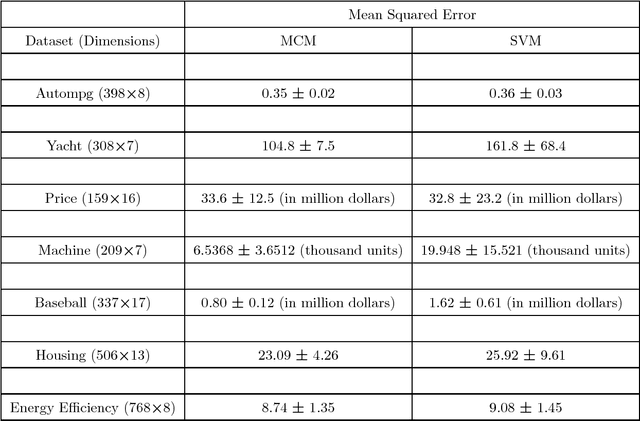
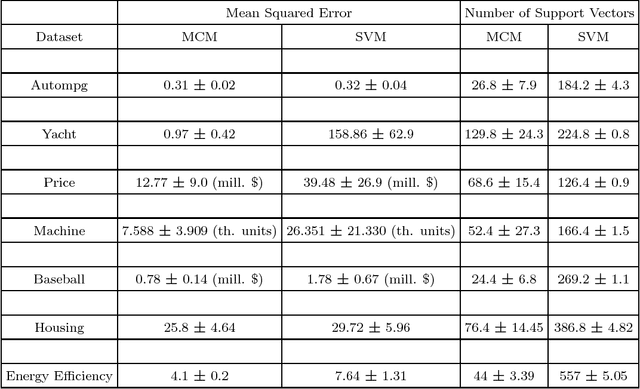
The capacity of a learning machine is measured by its Vapnik-Chervonenkis dimension, and learning machines with a low VC dimension generalize better. It is well known that the VC dimension of SVMs can be very large or unbounded, even though they generally yield state-of-the-art learning performance. In this paper, we show how to learn a hyperplane regressor by minimizing an exact, or \boldmath{$\Theta$} bound on its VC dimension. The proposed approach, termed as the Minimal Complexity Machine (MCM) Regressor, involves solving a simple linear programming problem. Experimental results show, that on a number of benchmark datasets, the proposed approach yields regressors with error rates much less than those obtained with conventional SVM regresssors, while often using fewer support vectors. On some benchmark datasets, the number of support vectors is less than one tenth the number used by SVMs, indicating that the MCM does indeed learn simpler representations.