Why is the winner the best?

International benchmarking competitions have become fundamental for the comparative performance assessment of image analysis methods. However, little attention has been given to investigating what can be learnt from these competitions. Do they really generate scientific progress? What are common and successful participation strategies? What makes a solution superior to a competing method? To address this gap in the literature, we performed a multi-center study with all 80 competitions that were conducted in the scope of IEEE ISBI 2021 and MICCAI 2021. Statistical analyses performed based on comprehensive descriptions of the submitted algorithms linked to their rank as well as the underlying participation strategies revealed common characteristics of winning solutions. These typically include the use of multi-task learning (63%) and/or multi-stage pipelines (61%), and a focus on augmentation (100%), image preprocessing (97%), data curation (79%), and postprocessing (66%). The "typical" lead of a winning team is a computer scientist with a doctoral degree, five years of experience in biomedical image analysis, and four years of experience in deep learning. Two core general development strategies stood out for highly-ranked teams: the reflection of the metrics in the method design and the focus on analyzing and handling failure cases. According to the organizers, 43% of the winning algorithms exceeded the state of the art but only 11% completely solved the respective domain problem. The insights of our study could help researchers (1) improve algorithm development strategies when approaching new problems, and (2) focus on open research questions revealed by this work.

Extending nn-UNet for brain tumor segmentation

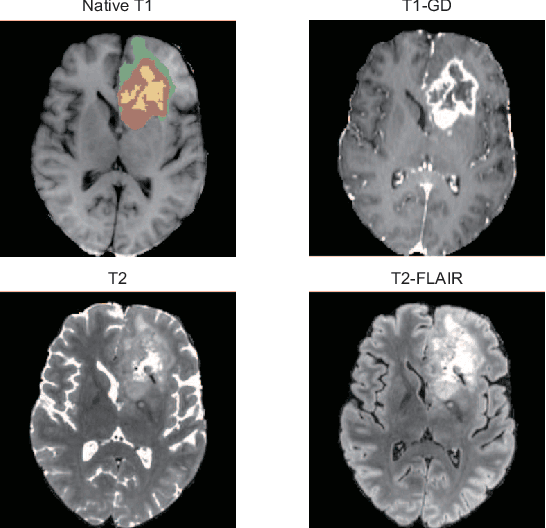
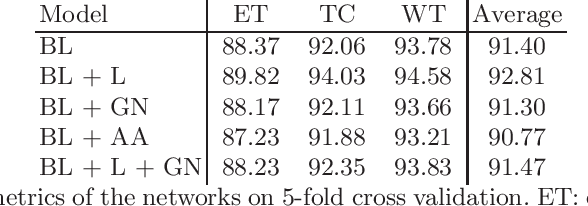
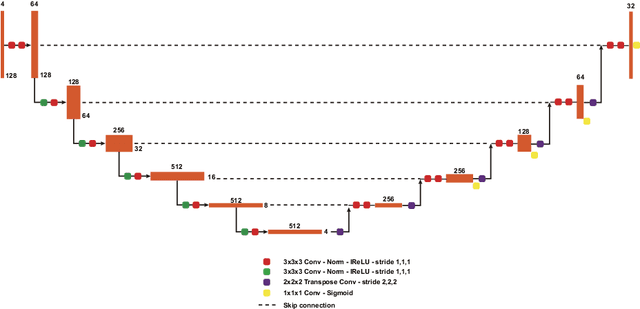
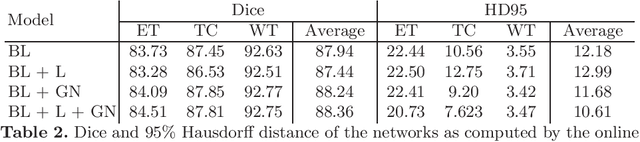
Brain tumor segmentation is essential for the diagnosis and prognosis of patients with gliomas. The brain tumor segmentation challenge has continued to provide a great source of data to develop automatic algorithms to perform the task. This paper describes our contribution to the 2021 competition. We developed our methods based on nn-UNet, the winning entry of last year competition. We experimented with several modifications, including using a larger network, replacing batch normalization with group normalization, and utilizing axial attention in the decoder. Internal 5-fold cross validation as well as online evaluation from the organizers showed the effectiveness of our approach, with minor improvement in quantitative metrics when compared to the baseline. The proposed models won first place in the final ranking on unseen test data. The codes, pretrained weights, and docker image for the winning submission are publicly available at https://github.com/rixez/Brats21_KAIST_MRI_Lab

CycleQSM: Unsupervised QSM Deep Learning using Physics-Informed CycleGAN

Quantitative susceptibility mapping (QSM) is a useful magnetic resonance imaging (MRI) technique which provides spatial distribution of magnetic susceptibility values of tissues. QSMs can be obtained by deconvolving the dipole kernel from phase images, but the spectral nulls in the dipole kernel make the inversion ill-posed. In recent times, deep learning approaches have shown a comparable QSM reconstruction performance as the classic approaches, despite the fast reconstruction time. Most of the existing deep learning methods are, however, based on supervised learning, so matched pairs of input phase images and the ground-truth maps are needed. Moreover, it was reported that the supervised learning often leads to underestimated QSM values. To address this, here we propose a novel unsupervised QSM deep learning method using physics-informed cycleGAN, which is derived from optimal transport perspective. In contrast to the conventional cycleGAN, our novel cycleGAN has only one generator and one discriminator thanks to the known dipole kernel. Experimental results confirm that the proposed method provides more accurate QSM maps compared to the existing deep learning approaches, and provide competitive performance to the best classical approaches despite the ultra-fast reconstruction.

Quantitative Susceptibility Map Reconstruction Using Annihilating Filter-based Low-Rank Hankel Matrix Approach

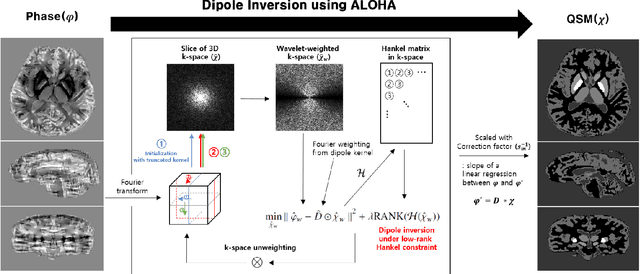
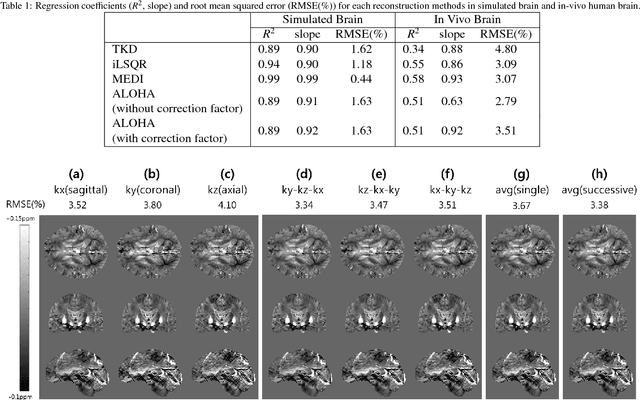
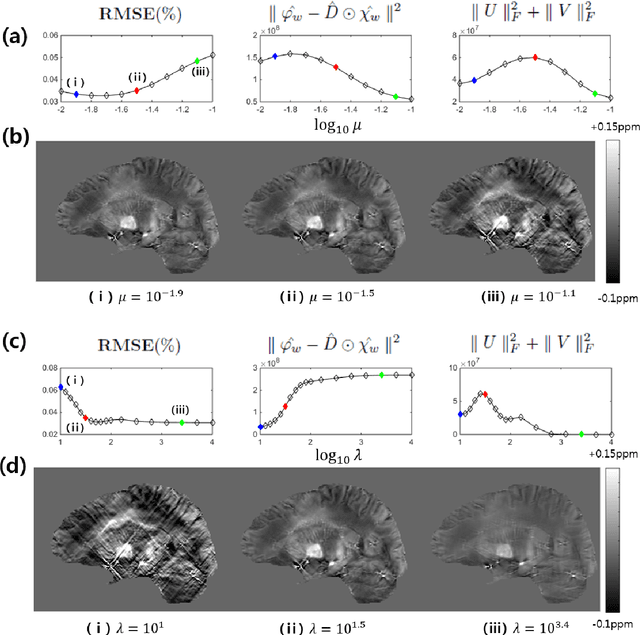
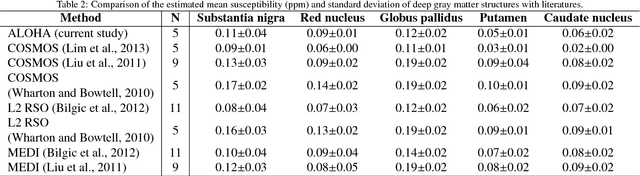
Quantitative susceptibility mapping (QSM) inevitably suffers from streaking artifacts caused by zeros on the conical surface of the dipole kernel in k-space. This work proposes a novel and accurate QSM reconstruction method based on a direct k-space interpolation approach, avoiding problems of over smoothing and streaking artifacts. Inspired by the recent theory of annihilating filter-based low-rank Hankel matrix approach (ALOHA), QSM reconstruction problem is formulated as deconvolution problem under low-rank Hankel matrix constraint in the k-space. To reduce the computational complexity and the memory requirement, the problem is formulated as successive reconstruction of 2-D planes along three independent axes of the 3-D phase image in Fourier domain. Extensive experiments were performed to verify and compare the proposed method with existing QSM reconstruction methods. The proposed ALOHA-QSM effectively reduced streaking artifacts and accurately estimated susceptibility values in deep gray matter structures, compared to the existing QSM methods. Our suggested ALOHA-QSM algorithm successfully solves the three-dimensional QSM dipole inversion problem without additional anatomical information or prior assumption and provides good image quality and quantitative accuracy.