A PAC-Bayesian Approach to Spectrally-Normalized Margin Bounds for Neural Networks

We present a generalization bound for feedforward neural networks in terms of the product of the spectral norm of the layers and the Frobenius norm of the weights. The generalization bound is derived using a PAC-Bayes analysis.

Exploring Generalization in Deep Learning

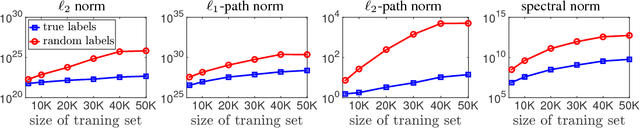
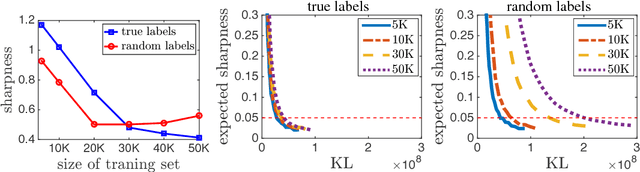
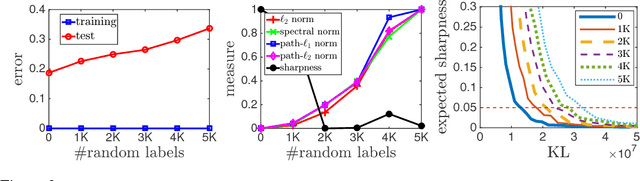
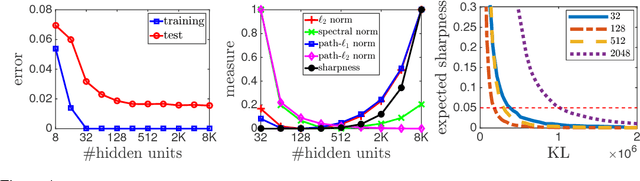
With a goal of understanding what drives generalization in deep networks, we consider several recently suggested explanations, including norm-based control, sharpness and robustness. We study how these measures can ensure generalization, highlighting the importance of scale normalization, and making a connection between sharpness and PAC-Bayes theory. We then investigate how well the measures explain different observed phenomena.

Implicit Regularization in Matrix Factorization

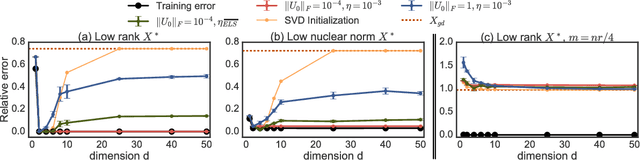
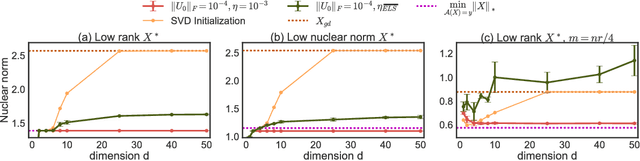
We study implicit regularization when optimizing an underdetermined quadratic objective over a matrix $X$ with gradient descent on a factorization of $X$. We conjecture and provide empirical and theoretical evidence that with small enough step sizes and initialization close enough to the origin, gradient descent on a full dimensional factorization converges to the minimum nuclear norm solution.

Single Pass PCA of Matrix Products

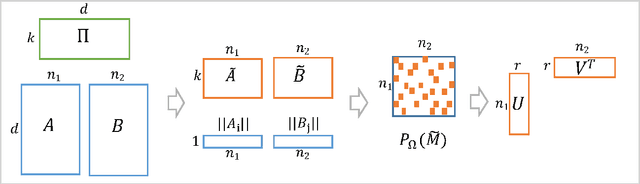
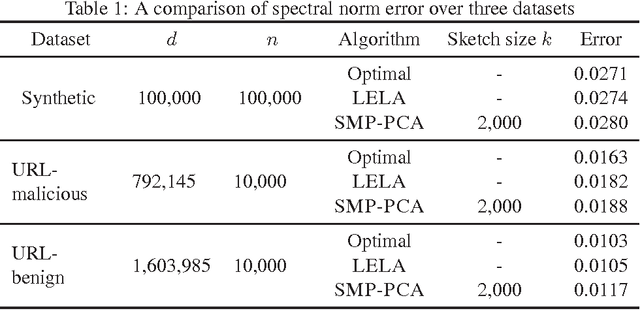
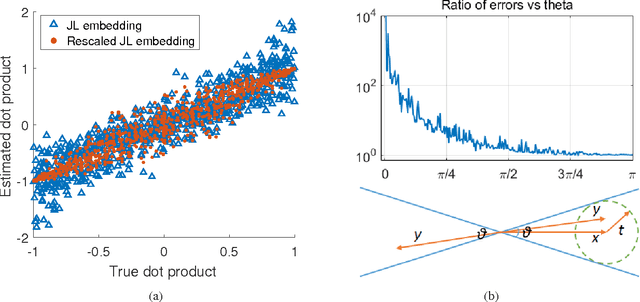
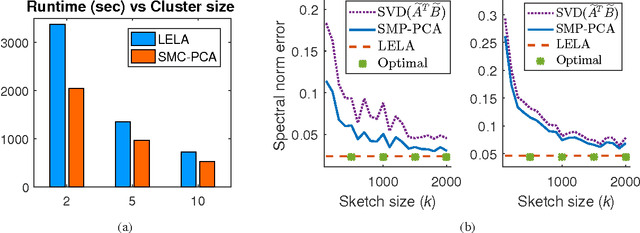
In this paper we present a new algorithm for computing a low rank approximation of the product $A^TB$ by taking only a single pass of the two matrices $A$ and $B$. The straightforward way to do this is to (a) first sketch $A$ and $B$ individually, and then (b) find the top components using PCA on the sketch. Our algorithm in contrast retains additional summary information about $A,B$ (e.g. row and column norms etc.) and uses this additional information to obtain an improved approximation from the sketches. Our main analytical result establishes a comparable spectral norm guarantee to existing two-pass methods; in addition we also provide results from an Apache Spark implementation that shows better computational and statistical performance on real-world and synthetic evaluation datasets.

Provable Burer-Monteiro factorization for a class of norm-constrained matrix problems

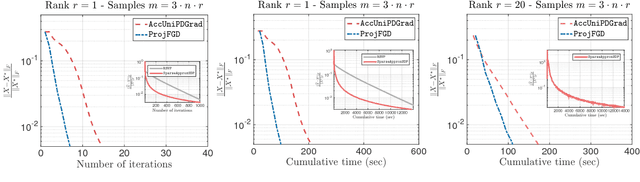
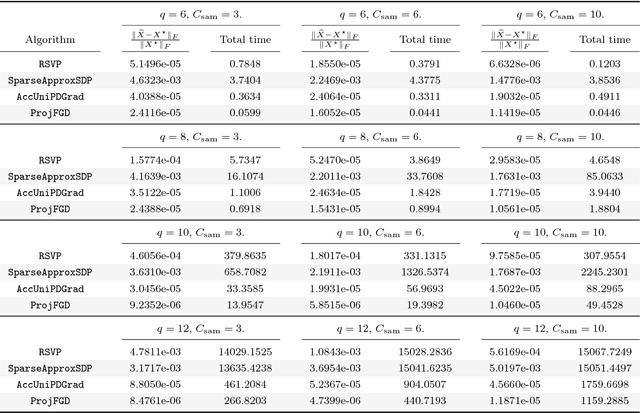
We study the projected gradient descent method on low-rank matrix problems with a strongly convex objective. We use the Burer-Monteiro factorization approach to implicitly enforce low-rankness; such factorization introduces non-convexity in the objective. We focus on constraint sets that include both positive semi-definite (PSD) constraints and specific matrix norm-constraints. Such criteria appear in quantum state tomography and phase retrieval applications. We show that non-convex projected gradient descent favors local linear convergence in the factored space. We build our theory on a novel descent lemma, that non-trivially extends recent results on the unconstrained problem. The resulting algorithm is Projected Factored Gradient Descent, abbreviated as ProjFGD, and shows superior performance compared to state of the art on quantum state tomography and sparse phase retrieval applications.

Global Optimality of Local Search for Low Rank Matrix Recovery

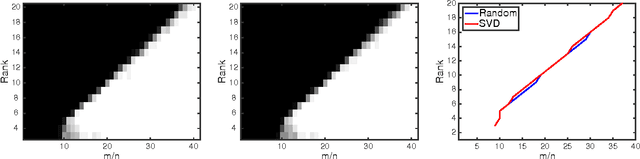
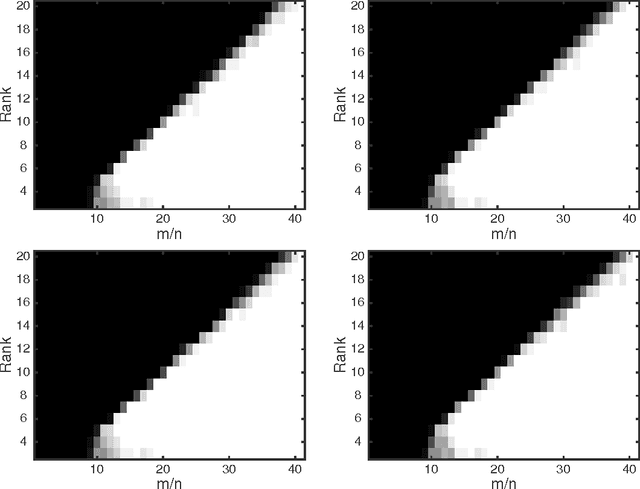
We show that there are no spurious local minima in the non-convex factorized parametrization of low-rank matrix recovery from incoherent linear measurements. With noisy measurements we show all local minima are very close to a global optimum. Together with a curvature bound at saddle points, this yields a polynomial time global convergence guarantee for stochastic gradient descent {\em from random initialization}.

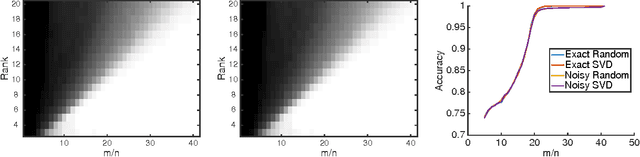
Dropping Convexity for Faster Semi-definite Optimization

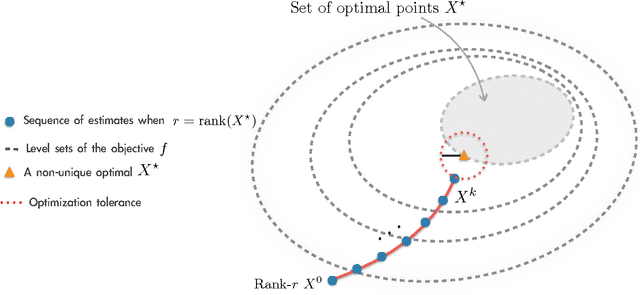
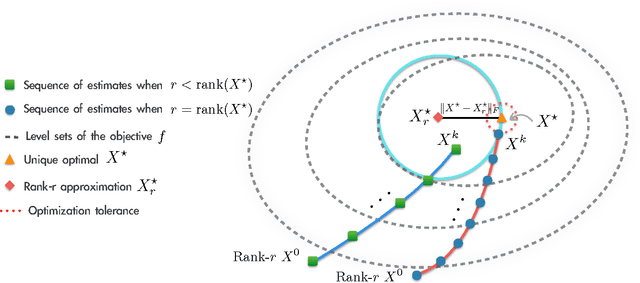
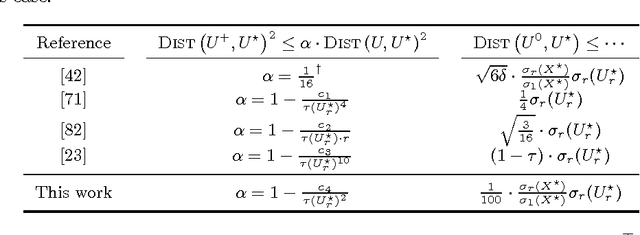
We study the minimization of a convex function $f(X)$ over the set of $n\times n$ positive semi-definite matrices, but when the problem is recast as $\min_U g(U) := f(UU^\top)$, with $U \in \mathbb{R}^{n \times r}$ and $r \leq n$. We study the performance of gradient descent on $g$---which we refer to as Factored Gradient Descent (FGD)---under standard assumptions on the original function $f$. We provide a rule for selecting the step size and, with this choice, show that the local convergence rate of FGD mirrors that of standard gradient descent on the original $f$: i.e., after $k$ steps, the error is $O(1/k)$ for smooth $f$, and exponentially small in $k$ when $f$ is (restricted) strongly convex. In addition, we provide a procedure to initialize FGD for (restricted) strongly convex objectives and when one only has access to $f$ via a first-order oracle; for several problem instances, such proper initialization leads to global convergence guarantees. FGD and similar procedures are widely used in practice for problems that can be posed as matrix factorization. To the best of our knowledge, this is the first paper to provide precise convergence rate guarantees for general convex functions under standard convex assumptions.

A New Sampling Technique for Tensors

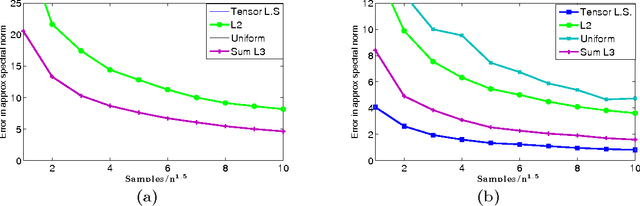
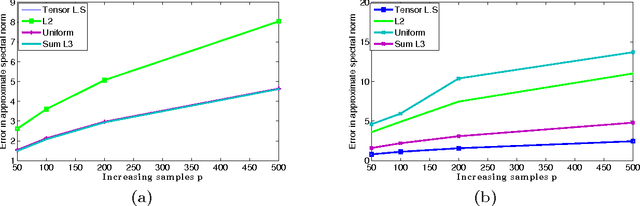
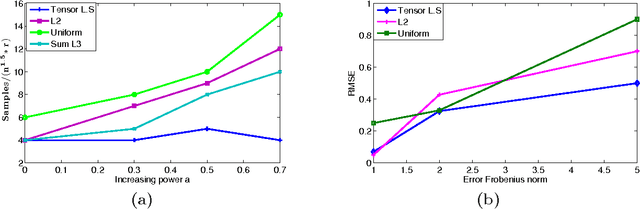
In this paper we propose new techniques to sample arbitrary third-order tensors, with an objective of speeding up tensor algorithms that have recently gained popularity in machine learning. Our main contribution is a new way to select, in a biased random way, only $O(n^{1.5}/\epsilon^2)$ of the possible $n^3$ elements while still achieving each of the three goals: \\ {\em (a) tensor sparsification}: for a tensor that has to be formed from arbitrary samples, compute very few elements to get a good spectral approximation, and for arbitrary orthogonal tensors {\em (b) tensor completion:} recover an exactly low-rank tensor from a small number of samples via alternating least squares, or {\em (c) tensor factorization:} approximating factors of a low-rank tensor corrupted by noise. \\ Our sampling can be used along with existing tensor-based algorithms to speed them up, removing the computational bottleneck in these methods.

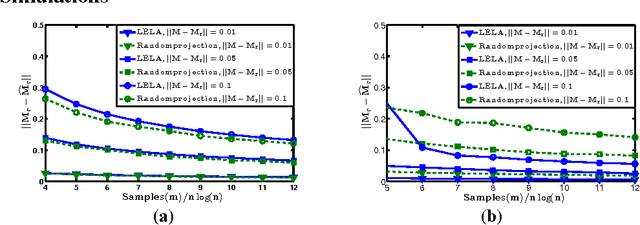
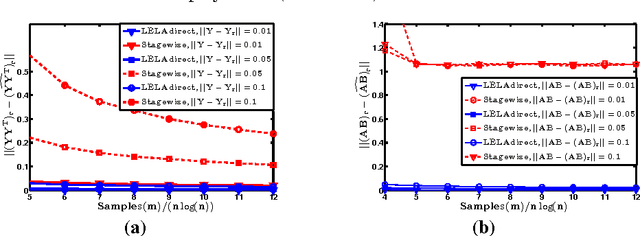
Tighter Low-rank Approximation via Sampling the Leveraged Element

In this work, we propose a new randomized algorithm for computing a low-rank approximation to a given matrix. Taking an approach different from existing literature, our method first involves a specific biased sampling, with an element being chosen based on the leverage scores of its row and column, and then involves weighted alternating minimization over the factored form of the intended low-rank matrix, to minimize error only on these samples. Our method can leverage input sparsity, yet produce approximations in {\em spectral} (as opposed to the weaker Frobenius) norm; this combines the best aspects of otherwise disparate current results, but with a dependence on the condition number $\kappa = \sigma_1/\sigma_r$. In particular we require $O(nnz(M) + \frac{n\kappa^2 r^5}{\epsilon^2})$ computations to generate a rank-$r$ approximation to $M$ in spectral norm. In contrast, the best existing method requires $O(nnz(M)+ \frac{nr^2}{\epsilon^4})$ time to compute an approximation in Frobenius norm. Besides the tightness in spectral norm, we have a better dependence on the error $\epsilon$. Our method is naturally and highly parallelizable. Our new approach enables two extensions that are interesting on their own. The first is a new method to directly compute a low-rank approximation (in efficient factored form) to the product of two given matrices; it computes a small random set of entries of the product, and then executes weighted alternating minimization (as before) on these. The sampling strategy is different because now we cannot access leverage scores of the product matrix (but instead have to work with input matrices). The second extension is an improved algorithm with smaller communication complexity for the distributed PCA setting (where each server has small set of rows of the matrix, and want to compute low rank approximation with small amount of communication with other servers).

Completing Any Low-rank Matrix, Provably

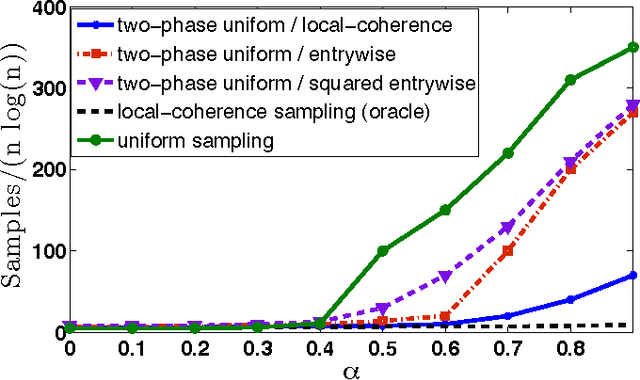
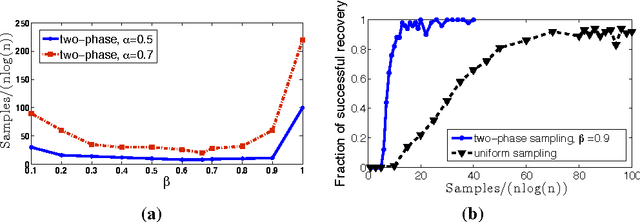
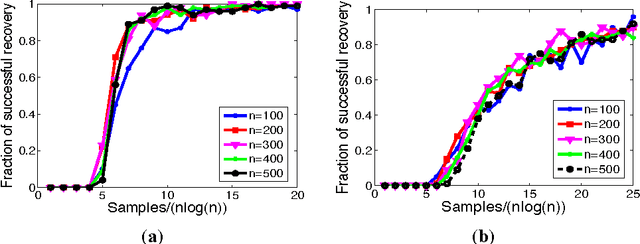
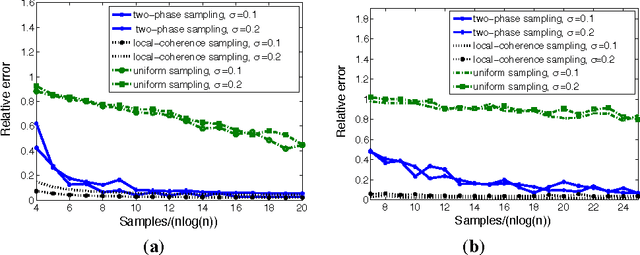
Matrix completion, i.e., the exact and provable recovery of a low-rank matrix from a small subset of its elements, is currently only known to be possible if the matrix satisfies a restrictive structural constraint---known as {\em incoherence}---on its row and column spaces. In these cases, the subset of elements is sampled uniformly at random. In this paper, we show that {\em any} rank-$ r $ $ n$-by-$ n $ matrix can be exactly recovered from as few as $O(nr \log^2 n)$ randomly chosen elements, provided this random choice is made according to a {\em specific biased distribution}: the probability of any element being sampled should be proportional to the sum of the leverage scores of the corresponding row, and column. Perhaps equally important, we show that this specific form of sampling is nearly necessary, in a natural precise sense; this implies that other perhaps more intuitive sampling schemes fail. We further establish three ways to use the above result for the setting when leverage scores are not known \textit{a priori}: (a) a sampling strategy for the case when only one of the row or column spaces are incoherent, (b) a two-phase sampling procedure for general matrices that first samples to estimate leverage scores followed by sampling for exact recovery, and (c) an analysis showing the advantages of weighted nuclear/trace-norm minimization over the vanilla un-weighted formulation for the case of non-uniform sampling.