Separation-Free Super-Resolution from Compressed Measurements is Possible: an Orthonormal Atomic Norm Minimization Approach

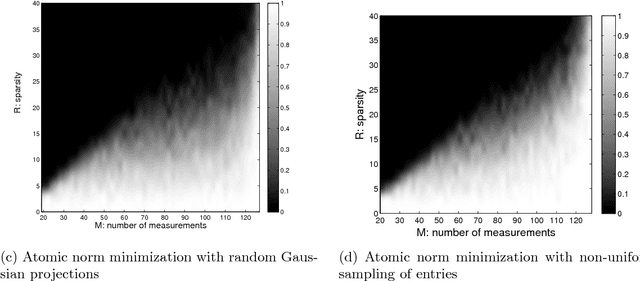
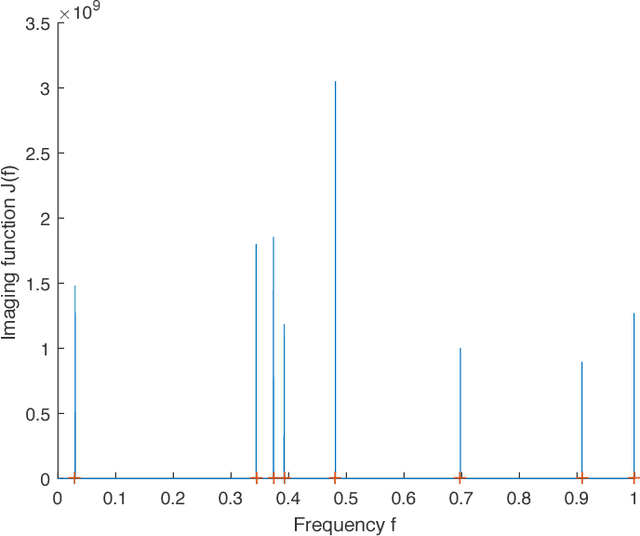
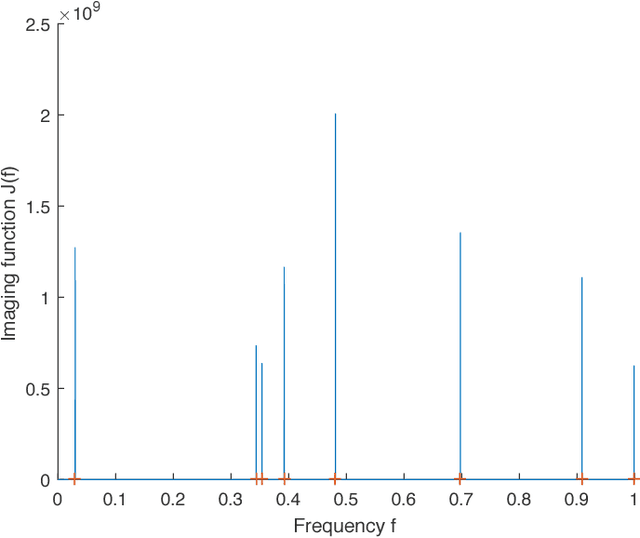
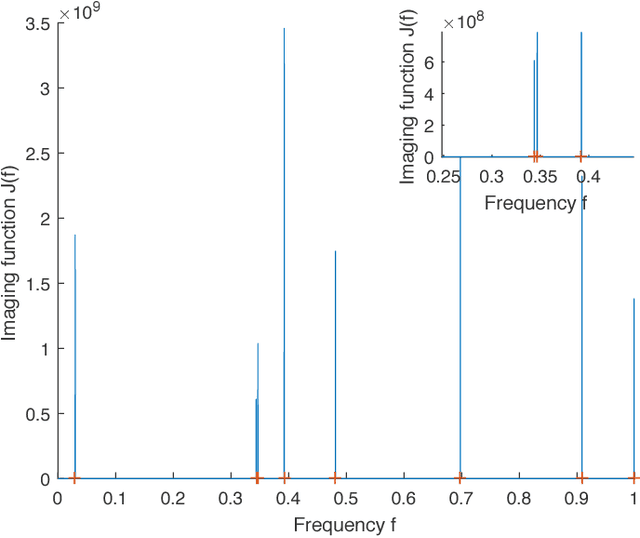
We consider the problem of recovering the superposition of $R$ distinct complex exponential functions from compressed non-uniform time-domain samples. Total Variation (TV) minimization or atomic norm minimization was proposed in the literature to recover the $R$ frequencies or the missing data. However, it is known that in order for TV minimization and atomic norm minimization to recover the missing data or the frequencies, the underlying $R$ frequencies are required to be well-separated, even when the measurements are noiseless. This paper shows that the Hankel matrix recovery approach can super-resolve the $R$ complex exponentials and their frequencies from compressed non-uniform measurements, regardless of how close their frequencies are to each other. We propose a new concept of orthonormal atomic norm minimization (OANM), and demonstrate that the success of Hankel matrix recovery in separation-free super-resolution comes from the fact that the nuclear norm of a Hankel matrix is an orthonormal atomic norm. More specifically, we show that, in traditional atomic norm minimization, the underlying parameter values $\textbf{must}$ be well separated to achieve successful signal recovery, if the atoms are changing continuously with respect to the continuously-valued parameter. In contrast, for the OANM, it is possible the OANM is successful even though the original atoms can be arbitrarily close. As a byproduct of this research, we provide one matrix-theoretic inequality of nuclear norm, and give its proof from the theory of compressed sensing.

Two step recovery of jointly sparse and low-rank matrices: theoretical guarantees

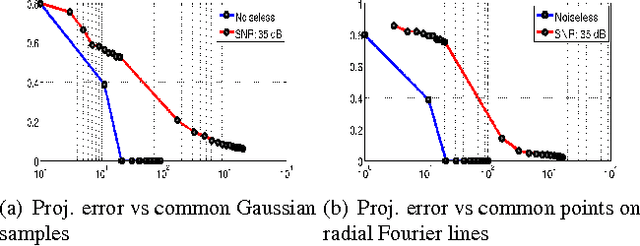
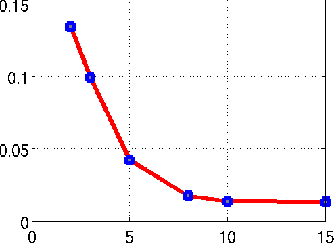
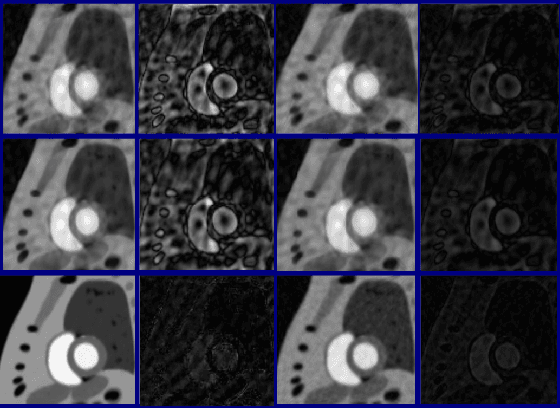
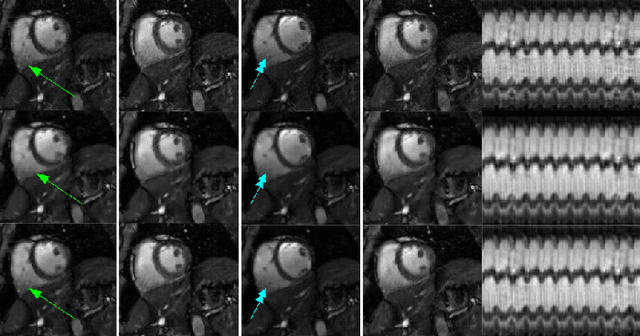
We introduce a two step algorithm with theoretical guarantees to recover a jointly sparse and low-rank matrix from undersampled measurements of its columns. The algorithm first estimates the row subspace of the matrix using a set of common measurements of the columns. In the second step, the subspace aware recovery of the matrix is solved using a simple least square algorithm. The results are verified in the context of recovering CINE data from undersampled measurements; we obtain good recovery when the sampling conditions are satisfied.

Subspace based low rank and joint sparse matrix recovery

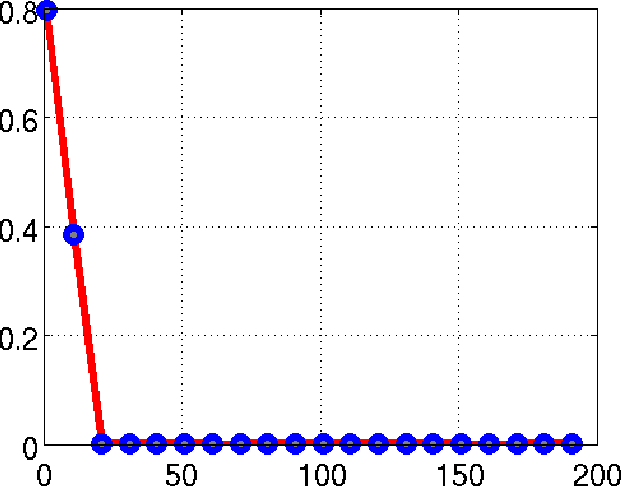
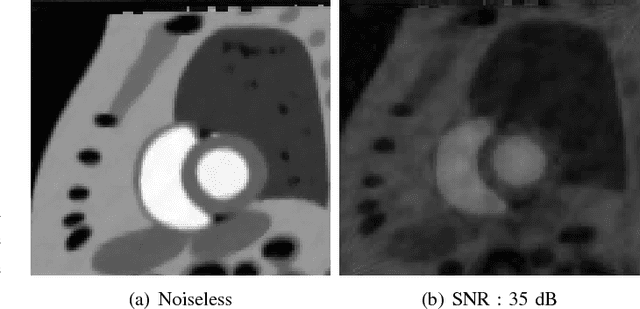
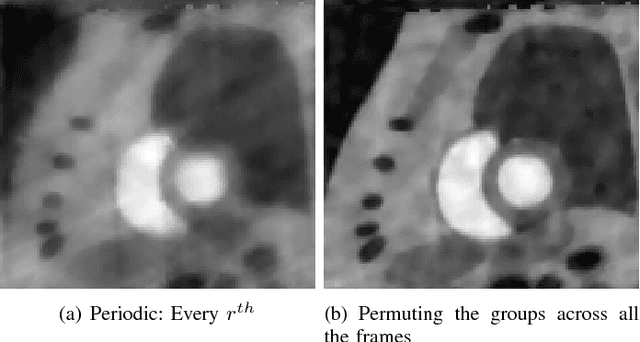
We consider the recovery of a low rank and jointly sparse matrix from under sampled measurements of its columns. This problem is highly relevant in the recovery of dynamic MRI data with high spatio-temporal resolution, where each column of the matrix corresponds to a frame in the image time series; the matrix is highly low-rank since the frames are highly correlated. Similarly the non-zero locations of the matrix in appropriate transform/frame domains (e.g. wavelet, gradient) are roughly the same in different frame. The superset of the support can be safely assumed to be jointly sparse. Unlike the classical multiple measurement vector (MMV) setup that measures all the snapshots using the same matrix, we consider each snapshot to be measured using a different measurement matrix. We show that this approach reduces the total number of measurements, especially when the rank of the matrix is much smaller than than its sparsity. Our experiments in the context of dynamic imaging shows that this approach is very useful in realizing free breathing cardiac MRI.