Separation-Free Super-Resolution from Compressed Measurements is Possible: an Orthonormal Atomic Norm Minimization Approach
Paper and Code
Nov 04, 2017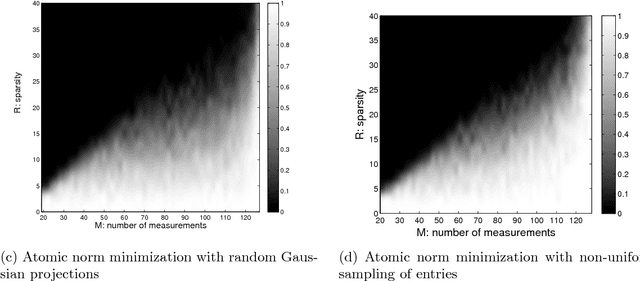
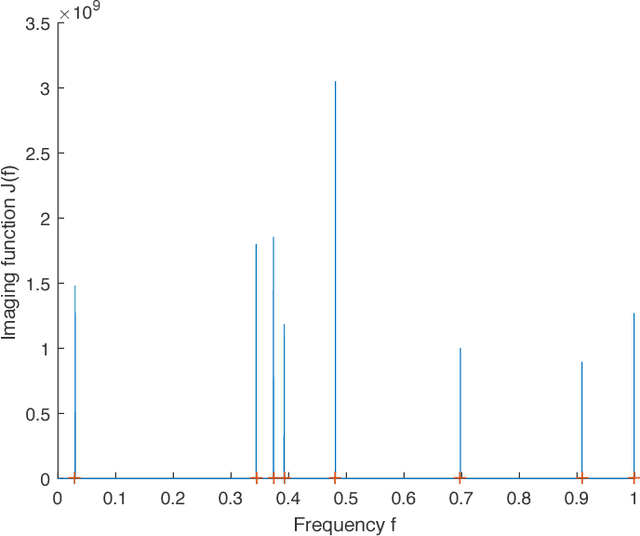
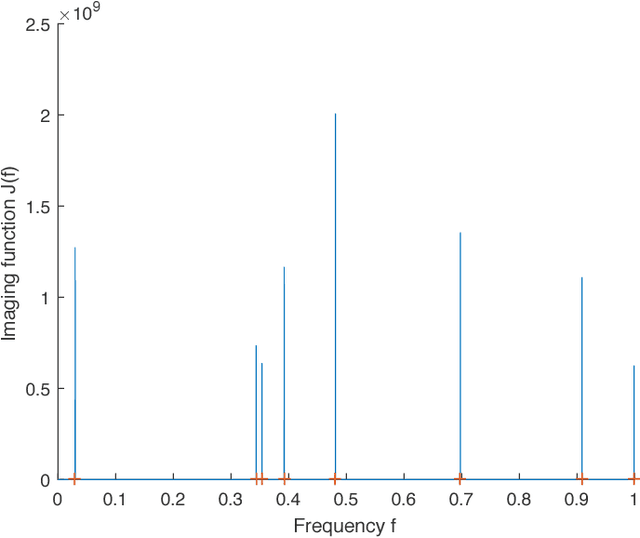
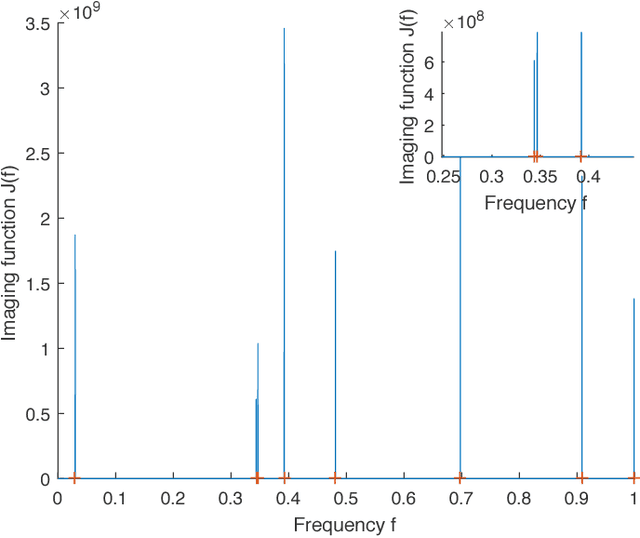
We consider the problem of recovering the superposition of $R$ distinct complex exponential functions from compressed non-uniform time-domain samples. Total Variation (TV) minimization or atomic norm minimization was proposed in the literature to recover the $R$ frequencies or the missing data. However, it is known that in order for TV minimization and atomic norm minimization to recover the missing data or the frequencies, the underlying $R$ frequencies are required to be well-separated, even when the measurements are noiseless. This paper shows that the Hankel matrix recovery approach can super-resolve the $R$ complex exponentials and their frequencies from compressed non-uniform measurements, regardless of how close their frequencies are to each other. We propose a new concept of orthonormal atomic norm minimization (OANM), and demonstrate that the success of Hankel matrix recovery in separation-free super-resolution comes from the fact that the nuclear norm of a Hankel matrix is an orthonormal atomic norm. More specifically, we show that, in traditional atomic norm minimization, the underlying parameter values $\textbf{must}$ be well separated to achieve successful signal recovery, if the atoms are changing continuously with respect to the continuously-valued parameter. In contrast, for the OANM, it is possible the OANM is successful even though the original atoms can be arbitrarily close. As a byproduct of this research, we provide one matrix-theoretic inequality of nuclear norm, and give its proof from the theory of compressed sensing.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge