SVRG Meets AdaGrad: Painless Variance Reduction

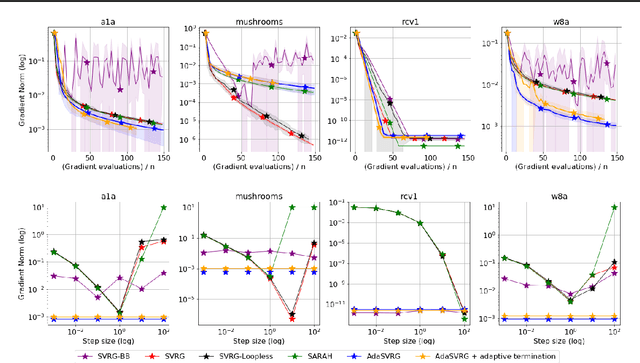
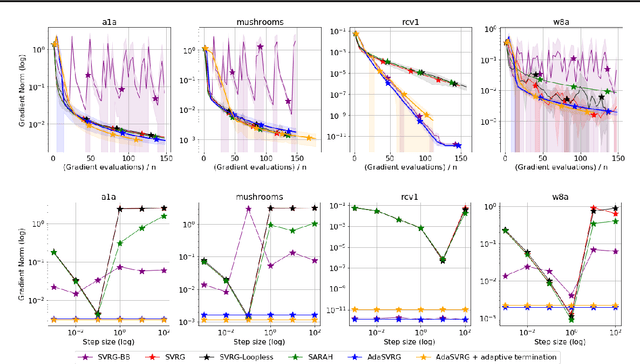
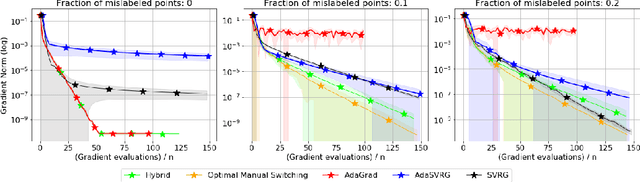
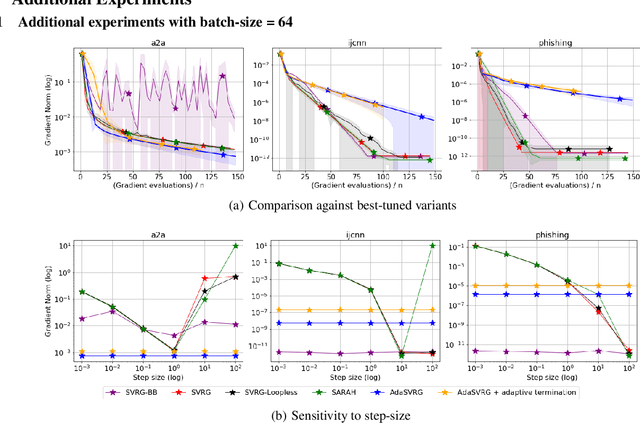
Variance reduction (VR) methods for finite-sum minimization typically require the knowledge of problem-dependent constants that are often unknown and difficult to estimate. To address this, we use ideas from adaptive gradient methods to propose AdaSVRG, which is a fully adaptive variant of SVRG, a common VR method. AdaSVRG uses AdaGrad in the inner loop of SVRG, making it robust to the choice of step-size, and allowing it to adaptively determine the length of each inner-loop. When minimizing a sum of $n$ smooth convex functions, we prove that AdaSVRG requires $O(n + 1/\epsilon)$ gradient evaluations to achieve an $\epsilon$-suboptimality, matching the typical rate, but without needing to know problem-dependent constants. However, VR methods including AdaSVRG are slower than SGD when used with over-parameterized models capable of interpolating the training data. Hence, we also propose a hybrid algorithm that can adaptively switch from AdaGrad to AdaSVRG, achieving the best of both stochastic gradient and VR methods, but without needing to tune their step-sizes. Via experiments on synthetic and standard real-world datasets, we validate the robustness and effectiveness of AdaSVRG, demonstrating its superior performance over other "tune-free" VR methods.

On the Convergence of Continuous Constrained Optimization for Structure Learning

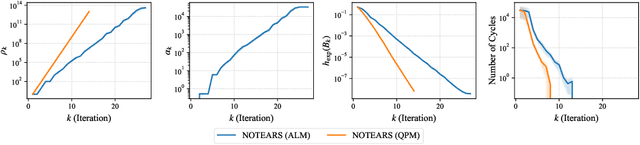
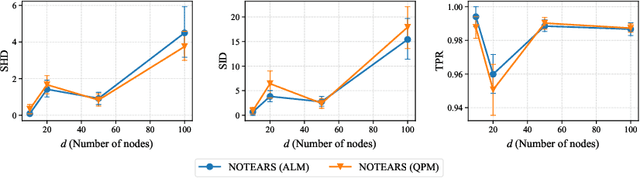
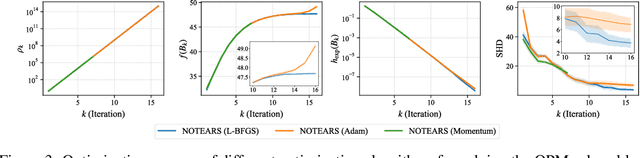
Structure learning of directed acyclic graphs (DAGs) is a fundamental problem in many scientific endeavors. A new line of work, based on NOTEARS (Zheng et al., 2018), reformulates the structure learning problem as a continuous optimization one by leveraging an algebraic characterization of DAG constraint. The constrained problem is typically solved using the augmented Lagrangian method (ALM) which is often preferred to the quadratic penalty method (QPM) by virtue of its convergence result that does not require the penalty coefficient to go to infinity, hence avoiding ill-conditioning. In this work, we review the standard convergence result of the ALM and show that the required conditions are not satisfied in the recent continuous constrained formulation for learning DAGs. We demonstrate empirically that its behavior is akin to that of the QPM which is prone to ill-conditioning, thus motivating the use of second-order method in this setting. We also establish the convergence guarantee of QPM to a DAG solution, under mild conditions, based on a property of the DAG constraint term.

Geometry-Aware Universal Mirror-Prox

Mirror-prox (MP) is a well-known algorithm to solve variational inequality (VI) problems. VI with a monotone operator covers a large group of settings such as convex minimization, min-max or saddle point problems. To get a convergent algorithm, the step-size of the classic MP algorithm relies heavily on the problem dependent knowledge of the operator such as its smoothness parameter which is hard to estimate. Recently, a universal variant of MP for smooth/bounded operators has been introduced that depends only on the norm of updates in MP. In this work, we relax the dependence to evaluating the norm of updates to Bregman divergence between updates. This relaxation allows us to extends the analysis of universal MP to the settings where the operator is not smooth or bounded. Furthermore, we analyse the VI problem with a stochastic monotone operator in different settings and obtain an optimal rate up to a logarithmic factor.

Machine Learning in Airline Crew Pairing to Construct Initial Clusters for Dynamic Constraint Aggregation

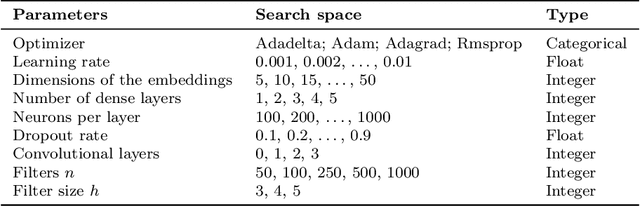
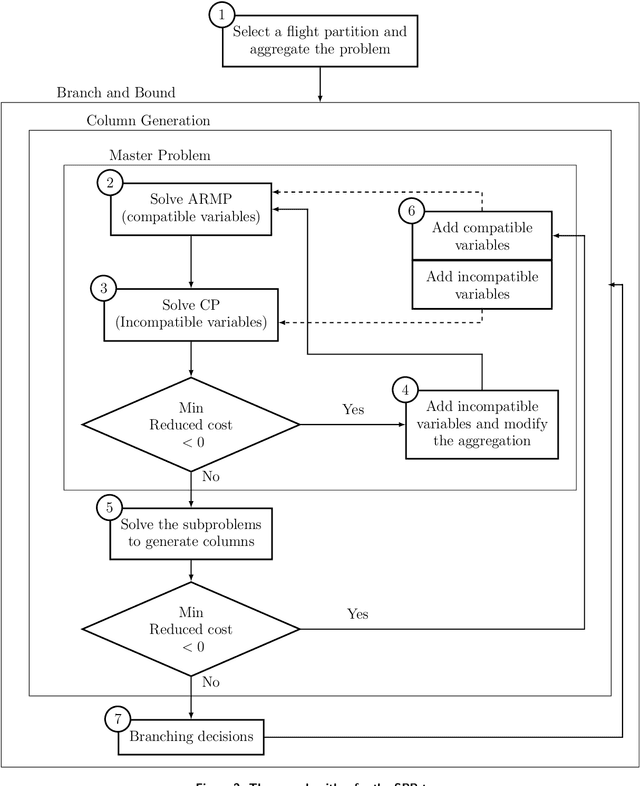
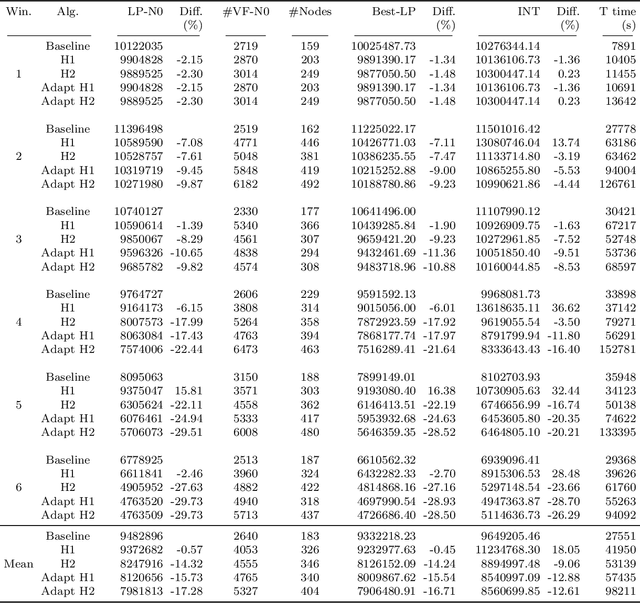
The crew pairing problem (CPP) is generally modelled as a set partitioning problem where the flights have to be partitioned in pairings. A pairing is a sequence of flight legs separated by connection time and rest periods that starts and ends at the same base. Because of the extensive list of complex rules and regulations, determining whether a sequence of flights constitutes a feasible pairing can be quite difficult by itself, making CPP one of the hardest of the airline planning problems. In this paper, we first propose to improve the prototype Baseline solver of Desaulniers et al. (2020) by adding dynamic control strategies to obtain an efficient solver for large-scale CPPs: Commercial-GENCOL-DCA. These solvers are designed to aggregate the flights covering constraints to reduce the size of the problem. Then, we use machine learning (ML) to produce clusters of flights having a high probability of being performed consecutively by the same crew. The solver combines several advanced Operations Research techniques to assemble and modify these clusters, when necessary, to produce a good solution. We show, on monthly CPPs with up to 50 000 flights, that Commercial-GENCOL-DCA with clusters produced by ML-based heuristics outperforms Baseline fed by initial clusters that are pairings of a solution obtained by rolling horizon with GENCOL. The reduction of solution cost averages between 6.8% and 8.52%, which is mainly due to the reduction in the cost of global constraints between 69.79% and 78.11%.

Flight-connection Prediction for Airline Crew Scheduling to Construct Initial Clusters for OR Optimizer

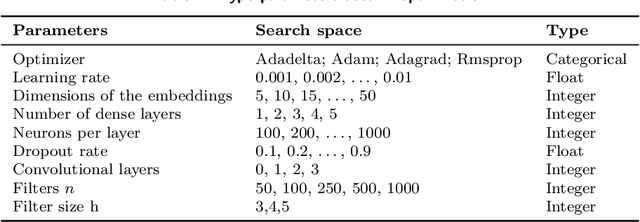
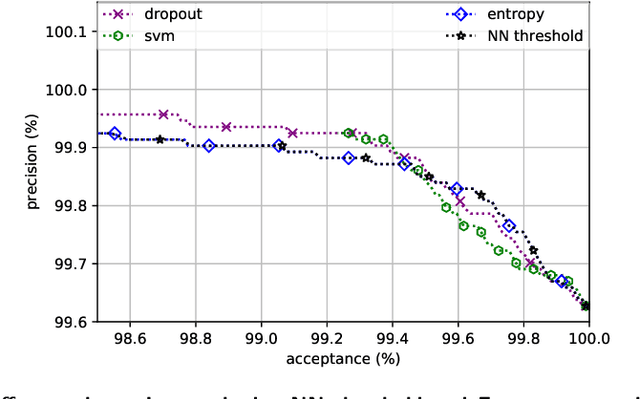
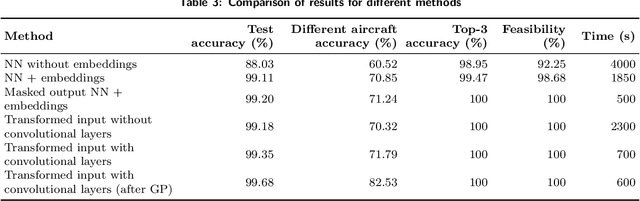
We present a case study of using machine learning classification algorithms to initialize a large scale commercial operations research solver (GENCOL) in the context of the airline crew pairing problem, where small savings of as little as 1% translate to increasing annual revenue by millions of dollars in a large airline. We focus on the problem of predicting the next connecting flight of a crew, framed as a multiclass classification problem trained from historical data, and design an adapted neural network approach that achieves high accuracy (99.7% overall or 82.5% on harder instances). We demonstrate the usefulness of our approach by using simple heuristics to combine the flight-connection predictions to form initial crew-pairing clusters that can be fed in the GENCOL solver, yielding a 10x speed improvement and up to 0.2% cost saving.

Implicit Regularization in Deep Learning: A View from Function Space

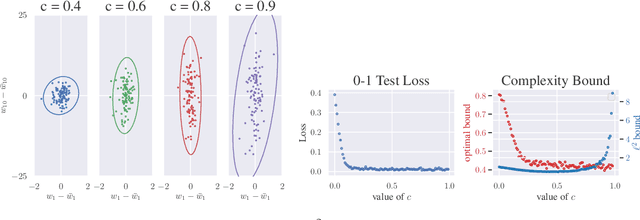
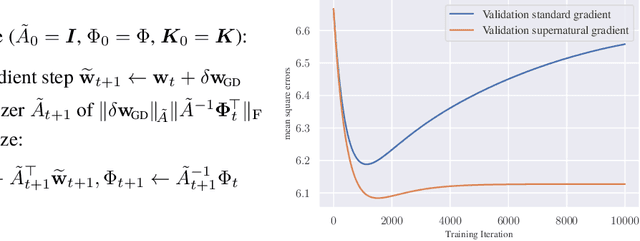
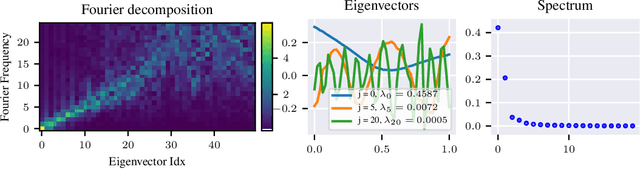
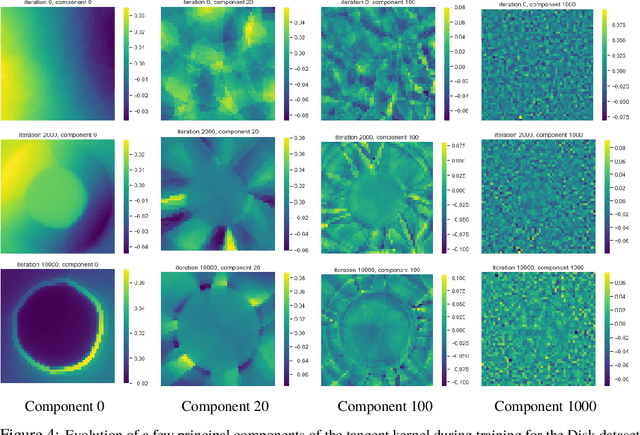
We approach the problem of implicit regularization in deep learning from a geometrical viewpoint. We highlight a possible regularization effect induced by a dynamical alignment of the neural tangent features introduced by Jacot et al, along a small number of task-relevant directions. By extrapolating a new analysis of Rademacher complexity bounds in linear models, we propose and study a new heuristic complexity measure for neural networks which captures this phenomenon, in terms of sequences of tangent kernel classes along in the learning trajectories.

Stochastic Hamiltonian Gradient Methods for Smooth Games

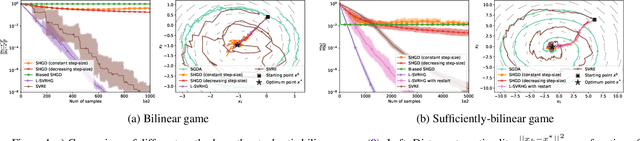
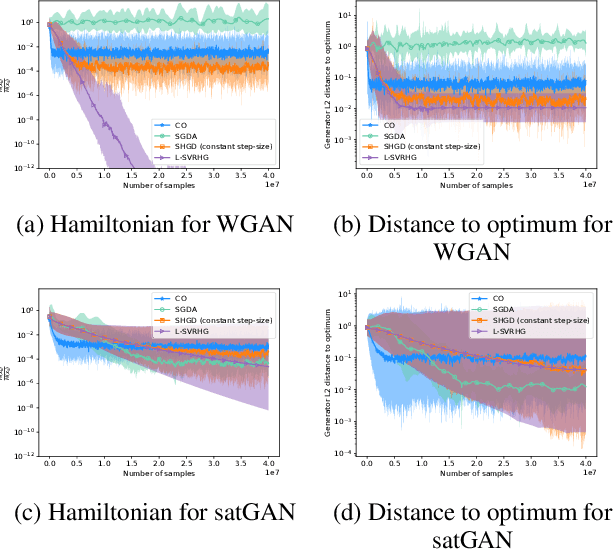
The success of adversarial formulations in machine learning has brought renewed motivation for smooth games. In this work, we focus on the class of stochastic Hamiltonian methods and provide the first convergence guarantees for certain classes of stochastic smooth games. We propose a novel unbiased estimator for the stochastic Hamiltonian gradient descent (SHGD) and highlight its benefits. Using tools from the optimization literature we show that SHGD converges linearly to the neighbourhood of a stationary point. To guarantee convergence to the exact solution, we analyze SHGD with a decreasing step-size and we also present the first stochastic variance reduced Hamiltonian method. Our results provide the first global non-asymptotic last-iterate convergence guarantees for the class of stochastic unconstrained bilinear games and for the more general class of stochastic games that satisfy a "sufficiently bilinear" condition, notably including some non-convex non-concave problems. We supplement our analysis with experiments on stochastic bilinear and sufficiently bilinear games, where our theory is shown to be tight, and on simple adversarial machine learning formulations.

Differentiable Causal Discovery from Interventional Data

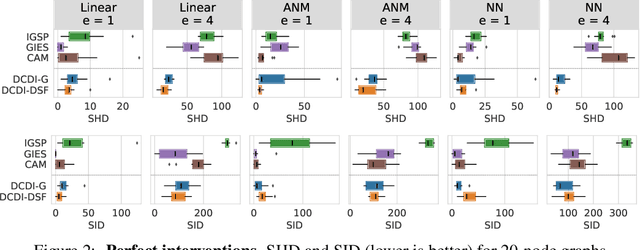
Discovering causal relationships in data is a challenging task that involves solving a combinatorial problem for which the solution is not always identifiable. A new line of work reformulates the combinatorial problem as a continuous constrained optimization one, enabling the use of different powerful optimization techniques. However, methods based on this idea do not yet make use of interventional data, which can significantly alleviate identifiability issues. In this work, we propose a neural network-based method for this task that can leverage interventional data. We illustrate the flexibility of the continuous-constrained framework by taking advantage of expressive neural architectures such as normalizing flows. We show that our approach compares favorably to the state of the art in a variety of settings, including perfect and imperfect interventions for which the targeted nodes may even be unknown.

Adversarial Example Games

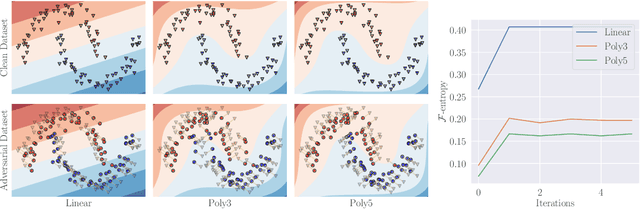
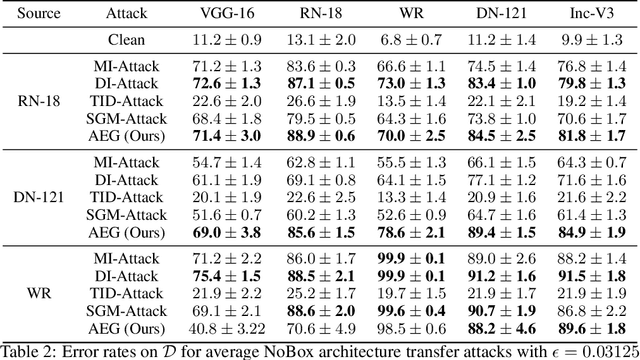
The existence of adversarial examples capable of fooling trained neural network classifiers calls for a much better understanding of possible attacks, in order to guide the development of safeguards against them. It includes attack methods in the highly challenging non-interactive blackbox setting, where adversarial attacks are generated without any access, including queries, to the target model. Prior works in this setting have relied mainly on algorithmic innovations derived from empirical observations (e.g., that momentum helps), and the field currently lacks a firm theoretical basis for understanding transferability in adversarial attacks. In this work, we address this gap and lay the theoretical foundations for crafting transferable adversarial examples to entire function classes. We introduce Adversarial Examples Games (AEG), a novel framework that models adversarial examples as two-player min-max games between an attack generator and a representative classifier. We prove that the saddle point of an AEG game corresponds to a generating distribution of adversarial examples against entire function classes. Training the generator only requires the ability to optimize a representative classifier from a given hypothesis class, enabling BlackBox transfer to unseen classifiers from the same class. We demonstrate the efficacy of our approach on the MNIST and CIFAR-10 datasets against both undefended and robustified models, achieving competitive performance with state-of-the-art BlackBox transfer approaches.

Adaptive Gradient Methods Converge Faster with Over-Parameterization (and you can do a line-search)

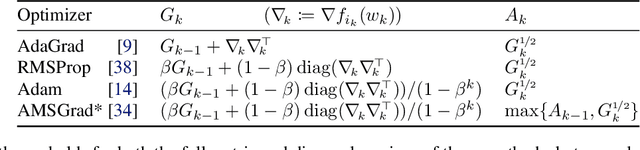
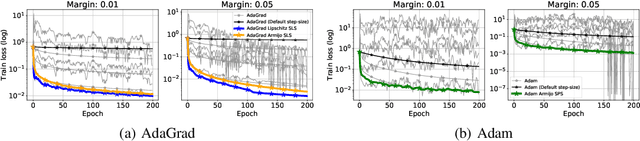
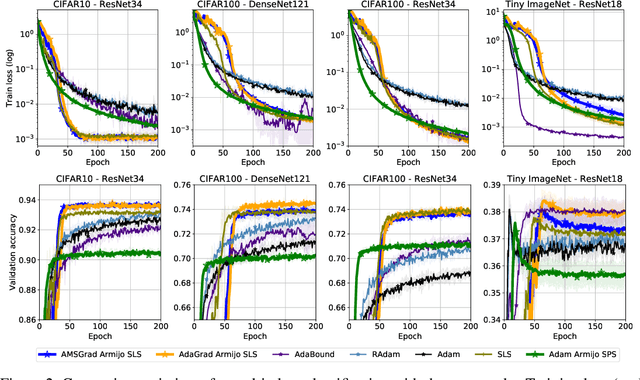
As adaptive gradient methods are typically used for training over-parameterized models capable of exactly fitting the data, we study their convergence in this interpolation setting. Under this assumption, we prove that constant step-size, zero-momentum variants of Adam and AMSGrad can converge to the minimizer at the O(1/T) rate for smooth, convex functions. When this assumption is only approximately satisfied, we show that these methods converge to a neighbourhood of the solution. On the other hand, we show that Adagrad is robust to the violation of interpolation and converges to the minimizer at the optimal rate. However, we demonstrate that even for simple, convex problems satisfying interpolation, the empirical performance of these methods heavily depends on the step-size and requires tuning. We alleviate this problem by making use of stochastic line-search methods (SLS) and Polyak's step-sizes (SPS) to help these methods adapt to the function's local smoothness. We prove that adaptive methods used in conjunction with these techniques do not require knowledge of problem-dependent constants and retain the convergence guarantees of their constant step-size counterparts. Experimentally, we show that using SLS or SPS consistently improves the convergence of adaptive methods across tasks; from binary classification with kernel mappings to classification with deep neural networks. Furthermore, our empirical results show that Adagrad equipped with SLS generalizes better than SGD.