SIEVE: Effective Filtered Vector Search with Collection of Indexes

Many real-world tasks such as recommending videos with the kids tag can be reduced to finding most similar vectors associated with hard predicates. This task, filtered vector search, is challenging as prior state-of-the-art graph-based (unfiltered) similarity search techniques quickly degenerate when hard constraints are considered. That is, effective graph-based filtered similarity search relies on sufficient connectivity for reaching the most similar items within just a few hops. To consider predicates, recent works propose modifying graph traversal to visit only the items that may satisfy predicates. However, they fail to offer the just-a-few-hops property for a wide range of predicates: they must restrict predicates significantly or lose efficiency if only a small fraction of items satisfy predicates. We propose an opposite approach: instead of constraining traversal, we build many indexes each serving different predicate forms. For effective construction, we devise a three-dimensional analytical model capturing relationships among index size, search time, and recall, with which we follow a workload-aware approach to pack as many useful indexes as possible into a collection. At query time, the analytical model is employed yet again to discern the one that offers the fastest search at a given recall. We show superior performance and support on datasets with varying selectivities and forms: our approach achieves up to 8.06x speedup while having as low as 1% build time versus other indexes, with less than 2.15x memory of a standard HNSW graph and modest knowledge of past workloads.

Cost Effective Optimization for Cost-related Hyperparameters

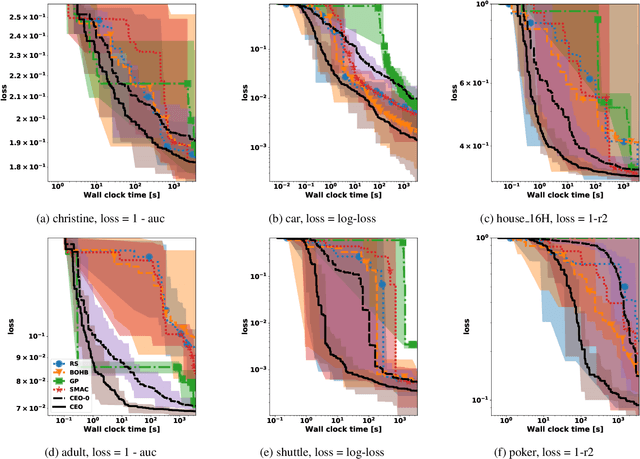
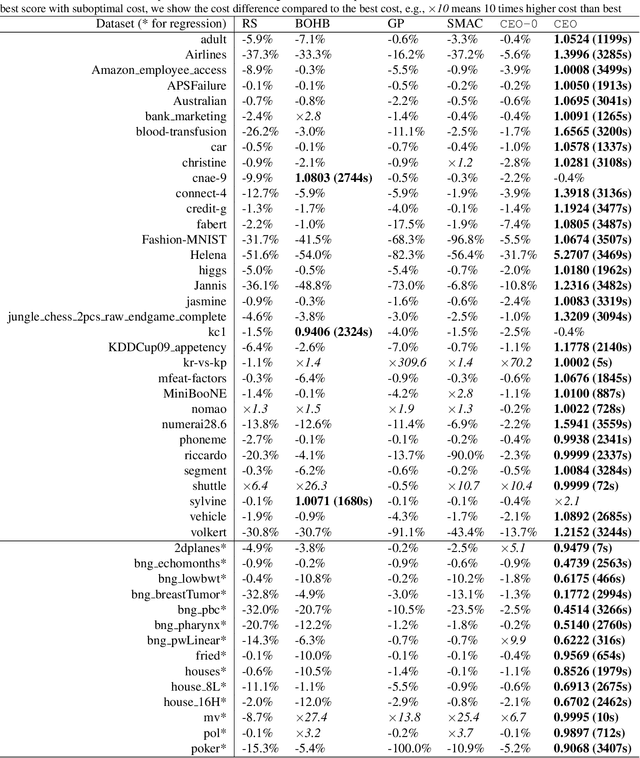
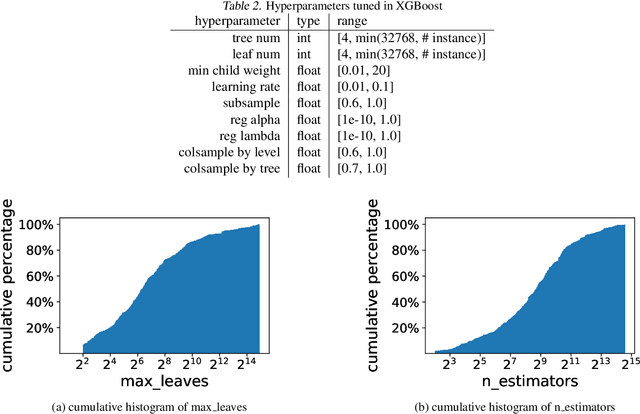
The increasing demand for democratizing machine learning algorithms for general software developers calls for hyperparameter optimization (HPO) solutions at low cost. Many machine learning algorithms have hyperparameters, which can cause a large variation in the training cost. But this effect is largely ignored in existing HPO methods, which are incapable to properly control cost during the optimization process. To address this problem, we develop a cost effective HPO solution. The core of our solution is a new randomized direct-search method. We prove a convergence rate of $O(\frac{\sqrt{d}}{\sqrt{K}})$ and provide an analysis on how it can be used to control evaluation cost under reasonable assumptions. Extensive evaluation using a latest AutoML benchmark shows a strong any time performance of the proposed HPO method when tuning cost-related hyperparameters.

Efficient Identification of Approximate Best Configuration of Training in Large Datasets

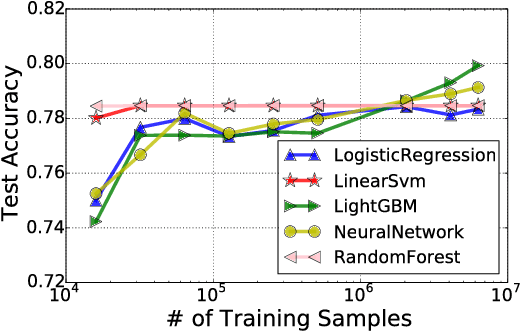
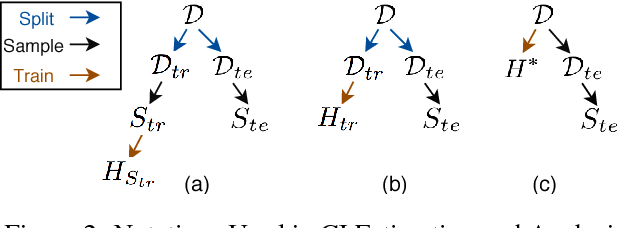
A configuration of training refers to the combinations of feature engineering, learner, and its associated hyperparameters. Given a set of configurations and a large dataset randomly split into training and testing set, we study how to efficiently identify the best configuration with approximately the highest testing accuracy when trained from the training set. To guarantee small accuracy loss, we develop a solution using confidence interval (CI)-based progressive sampling and pruning strategy. Compared to using full data to find the exact best configuration, our solution achieves more than two orders of magnitude speedup, while the returned top configuration has identical or close test accuracy.