The Dynamics of Gradient Descent for Overparametrized Neural Networks

We consider the dynamics of gradient descent (GD) in overparameterized single hidden layer neural networks with a squared loss function. Recently, it has been shown that, under some conditions, the parameter values obtained using GD achieve zero training error and generalize well if the initial conditions are chosen appropriately. Here, through a Lyapunov analysis, we show that the dynamics of neural network weights under GD converge to a point which is close to the minimum norm solution subject to the condition that there is no training error when using the linear approximation to the neural network. To illustrate the application of this result, we show that the GD converges to a prediction function that generalizes well, thereby providing an alternative proof of the generalization results in Arora et al. (2019).

Sample Complexity and Overparameterization Bounds for Projection-Free Neural TD Learning

We study the dynamics of temporal-difference learning with neural network-based value function approximation over a general state space, namely, \emph{Neural TD learning}. Existing analysis of neural TD learning relies on either infinite width-analysis or constraining the network parameters in a (random) compact set; as a result, an extra projection step is required at each iteration. This paper establishes a new convergence analysis of neural TD learning \emph{without any projection}. We show that the projection-free TD learning equipped with a two-layer ReLU network of any width exceeding $poly(\overline{\nu},1/\epsilon)$ converges to the true value function with error $\epsilon$ given $poly(\overline{\nu},1/\epsilon)$ iterations or samples, where $\overline{\nu}$ is an upper bound on the RKHS norm of the value function induced by the neural tangent kernel. Our sample complexity and overparameterization bounds are based on a drift analysis of the network parameters as a stopped random process in the lazy training regime.

Learning Latent Events from Network Message Logs: A Decomposition Based Approach

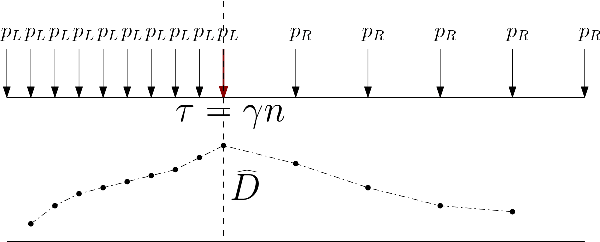
In this communication, we describe a novel technique for event mining using a decomposition based approach that combines non-parametric change-point detection with LDA. We prove theoretical guarantees about sample-complexity and consistency of the approach. In a companion paper, we will perform a thorough evaluation of our approach with detailed experiments.

Group-Sparse Model Selection: Hardness and Relaxations

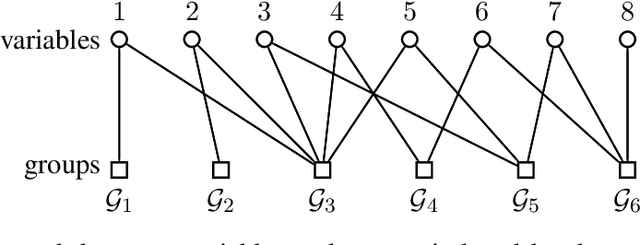
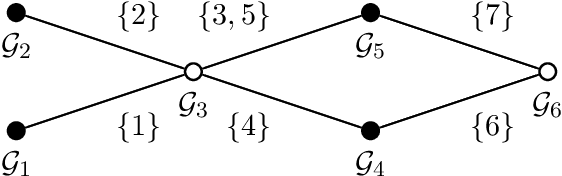
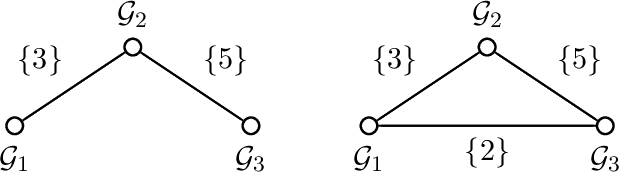
Group-based sparsity models are proven instrumental in linear regression problems for recovering signals from much fewer measurements than standard compressive sensing. The main promise of these models is the recovery of "interpretable" signals through the identification of their constituent groups. In this paper, we establish a combinatorial framework for group-model selection problems and highlight the underlying tractability issues. In particular, we show that the group-model selection problem is equivalent to the well-known NP-hard weighted maximum coverage problem (WMC). Leveraging a graph-based understanding of group models, we describe group structures which enable correct model selection in polynomial time via dynamic programming. Furthermore, group structures that lead to totally unimodular constraints have tractable discrete as well as convex relaxations. We also present a generalization of the group-model that allows for within group sparsity, which can be used to model hierarchical sparsity. Finally, we study the Pareto frontier of group-sparse approximations for two tractable models, among which the tree sparsity model, and illustrate selection and computation trade-offs between our framework and the existing convex relaxations.