Learning to Advect: A Neural Semi-Lagrangian Architecture for Weather Forecasting

Recent machine-learning approaches to weather forecasting often employ a monolithic architecture, where distinct physical mechanisms (advection, transport), diffusion-like mixing, thermodynamic processes, and forcing are represented implicitly within a single large network. This representation is particularly problematic for advection, where long-range transport must be treated with expensive global interaction mechanisms or through deep, stacked convolutional layers. To mitigate this, we present PARADIS, a physics-inspired global weather prediction model that imposes inductive biases on network behavior through a functional decomposition into advection, diffusion, and reaction blocks acting on latent variables. We implement advection through a Neural Semi-Lagrangian operator that performs trajectory-based transport via differentiable interpolation on the sphere, enabling end-to-end learning of both the latent modes to be transported and their characteristic trajectories. Diffusion-like processes are modeled through depthwise-separable spatial mixing, while local source terms and vertical interactions are modeled via pointwise channel interactions, enabling operator-level physical structure. PARADIS provides state-of-the-art forecast skill at a fraction of the training cost. On ERA5-based benchmarks, the 1 degree PARADIS model, with a total training cost of less than a GPU month, meets or exceeds the performance of 0.25 degree traditional and machine-learning baselines, including the ECMWF HRES forecast and DeepMind's GraphCast.

Probabilistic Forecasting for Dynamical Systems with Missing or Imperfect Data

The modeling of dynamical systems is essential in many fields, but applying machine learning techniques is often challenging due to incomplete or noisy data. This study introduces a variant of stochastic interpolation (SI) for probabilistic forecasting, estimating future states as distributions rather than single-point predictions. We explore its mathematical foundations and demonstrate its effectiveness on various dynamical systems, including the challenging WeatherBench dataset.

Advection Augmented Convolutional Neural Networks

Many problems in physical sciences are characterized by the prediction of space-time sequences. Such problems range from weather prediction to the analysis of disease propagation and video prediction. Modern techniques for the solution of these problems typically combine Convolution Neural Networks (CNN) architecture with a time prediction mechanism. However, oftentimes, such approaches underperform in the long-range propagation of information and lack explainability. In this work, we introduce a physically inspired architecture for the solution of such problems. Namely, we propose to augment CNNs with advection by designing a novel semi-Lagrangian push operator. We show that the proposed operator allows for the non-local transformation of information compared with standard convolutional kernels. We then complement it with Reaction and Diffusion neural components to form a network that mimics the Reaction-Advection-Diffusion equation, in high dimensions. We demonstrate the effectiveness of our network on a number of spatio-temporal datasets that show their merit.

Airfoil Shape Optimization using Deep Q-Network

The feasibility of using reinforcement learning for airfoil shape optimization is explored. Deep Q-Network (DQN) is used over Markov's decision process to find the optimal shape by learning the best changes to the initial shape for achieving the required goal. The airfoil profile is generated using Bezier control points to reduce the number of control variables. The changes in the position of control points are restricted to the direction normal to the chordline so as to reduce the complexity of optimization. The process is designed as a search for an episode of change done to each control point of a profile. The DQN essentially learns the episode of best changes by updating the temporal difference of the Bellman Optimality Equation. The drag and lift coefficients are calculated from the distribution of pressure coefficient along the profile computed using XFoil potential flow solver. These coefficients are used to give a reward to every change during the learning process where the ultimate aim stands to maximize the cumulate reward of an episode.

Numerical Approximation in CFD Problems Using Physics Informed Machine Learning

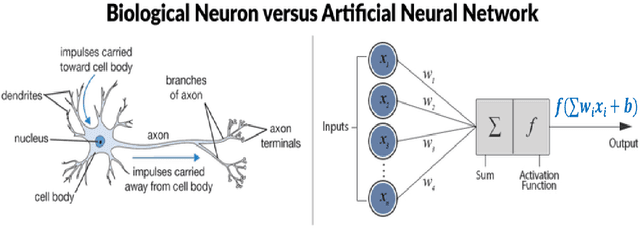
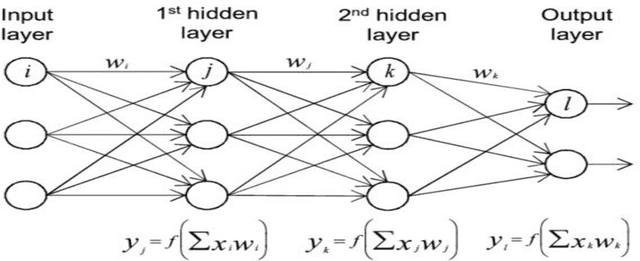
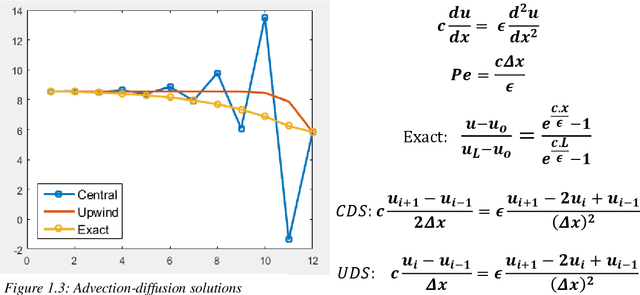
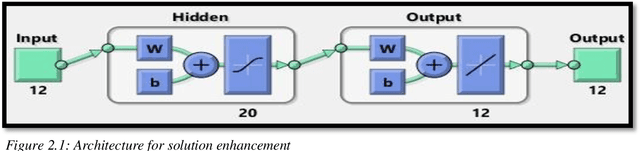
The thesis focuses on various techniques to find an alternate approximation method that could be universally used for a wide range of CFD problems but with low computational cost and low runtime. Various techniques have been explored within the field of machine learning to gauge the utility in fulfilling the core ambition. Steady advection diffusion problem has been used as the test case to understand the level of complexity up to which a method can provide solution. Ultimately, the focus stays over physics informed machine learning techniques where solving differential equations is possible without any training with computed data. The prevalent methods by I.E. Lagaris et.al. and M. Raissi et.al are explored thoroughly. The prevalent methods cannot solve advection dominant problems. A physics informed method, called as Distributed Physics Informed Neural Network (DPINN), is proposed to solve advection dominant problems. It increases the lexibility and capability of older methods by splitting the domain and introducing other physics-based constraints as mean squared loss terms. Various experiments are done to explore the end to end possibilities with the method. Parametric study is also done to understand the behavior of the method to different tunable parameters. The method is tested over steady advection-diffusion problems and unsteady square pulse problems. Very accurate results are recorded. Extreme learning machine (ELM) is a very fast neural network algorithm at the cost of tunable parameters. The ELM based variant of the proposed model is tested over the advection-diffusion problem. ELM makes the complex optimization simpler and Since the method is non-iterative, the solution is recorded in a single shot. The ELM based variant seems to work better than the simple DPINN method. Simultaneously scope for various development in future are hinted throughout the thesis.