SDIGLM: Leveraging Large Language Models and Multi-Modal Chain of Thought for Structural Damage Identification

Existing computer vision(CV)-based structural damage identification models demonstrate notable accuracy in categorizing and localizing damage. However, these models present several critical limitations that hinder their practical application in civil engineering(CE). Primarily, their ability to recognize damage types remains constrained, preventing comprehensive analysis of the highly varied and complex conditions encountered in real-world CE structures. Second, these models lack linguistic capabilities, rendering them unable to articulate structural damage characteristics through natural language descriptions. With the continuous advancement of artificial intelligence(AI), large multi-modal models(LMMs) have emerged as a transformative solution, enabling the unified encoding and alignment of textual and visual data. These models can autonomously generate detailed descriptive narratives of structural damage while demonstrating robust generalization across diverse scenarios and tasks. This study introduces SDIGLM, an innovative LMM for structural damage identification, developed based on the open-source VisualGLM-6B architecture. To address the challenge of adapting LMMs to the intricate and varied operating conditions in CE, this work integrates a U-Net-based semantic segmentation module to generate defect segmentation maps as visual Chain of Thought(CoT). Additionally, a multi-round dialogue fine-tuning dataset is constructed to enhance logical reasoning, complemented by a language CoT formed through prompt engineering. By leveraging this multi-modal CoT, SDIGLM surpasses general-purpose LMMs in structural damage identification, achieving an accuracy of 95.24% across various infrastructure types. Moreover, the model effectively describes damage characteristics such as hole size, crack direction, and corrosion severity.

A robust deep learning-based damage identification approach for SHM considering missing data

Data-driven method for Structural Health Monitoring (SHM), that mine the hidden structural performance from the correlations among monitored time series data, has received widely concerns recently. However, missing data significantly impacts the conduction of this method. Missing data is a frequently encountered issue in time series data in SHM and many other real-world applications, that harms to the standardized data mining and downstream tasks, such as condition assessment. Imputation approaches based on spatiotemporal relations among monitoring data are developed to handle this issue, however, no additional information is added during imputation. This paper thus develops a robust method for damage identification that considers the missing data occasions, based on long-short term memory (LSTM) model and dropout mechanism in the autoencoder (AE) framework. Inputs channels are randomly dropped to simulate the missing data in training, and reconstruction errors are used as the loss function and the damage indicator. Quasi-static response (cable tension) of a cable-stayed bridge released in 1st IPC-SHM is employed to verify this proposed method, and results show that the missing data imputation and damage identification can be implemented together in a unified way.

General solutions for nonlinear differential equations: a deep reinforcement learning approach

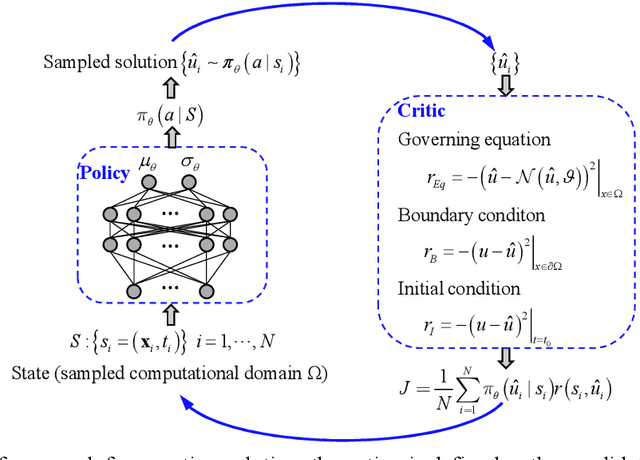
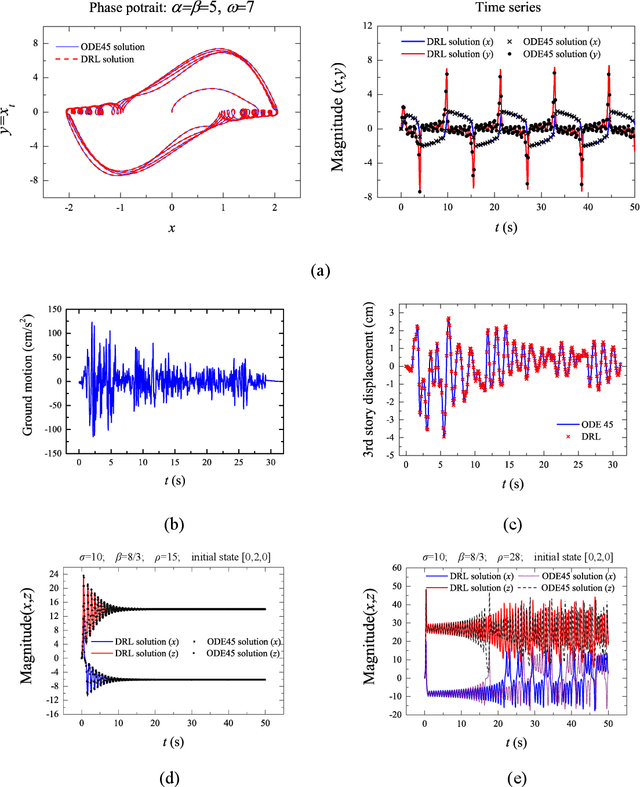
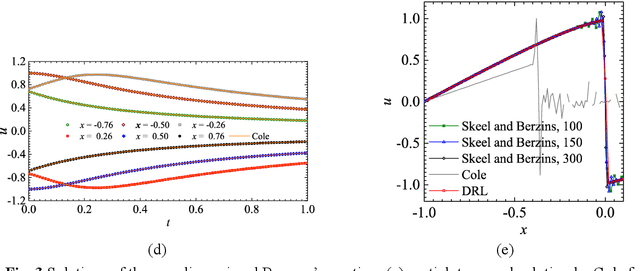
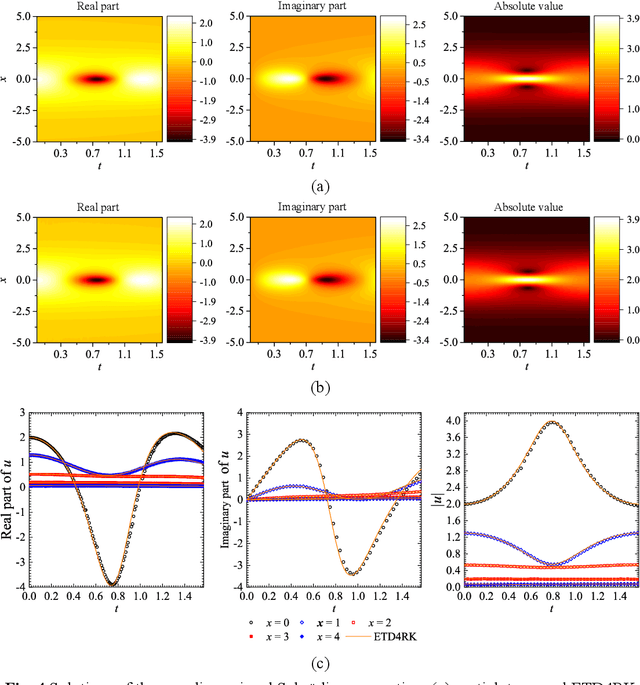
Physicists use differential equations to describe the physical dynamical world, and the solutions of these equations constitute our understanding of the world. During the hundreds of years, scientists developed several ways to solve these equations, i.e., the analytical solutions and the numerical solutions. However, for some complex equations, there may be no analytical solutions, and the numerical solutions may encounter the curse of the extreme computational cost if the accuracy is the first consideration. Solving equations is a high-level human intelligence work and a crucial step towards general artificial intelligence (AI), where deep reinforcement learning (DRL) may contribute. This work makes the first attempt of applying (DRL) to solve nonlinear differential equations both in discretized and continuous format with the governing equations (physical laws) embedded in the DRL network, including ordinary differential equations (ODEs) and partial differential equations (PDEs). The DRL network consists of an actor that outputs solution approximations policy and a critic that outputs the critic of the actor's output solution. Deterministic policy network is employed as the actor, and governing equations are embedded in the critic. The effectiveness of the DRL solver in Schr\"odinger equation, Navier-Stocks, Van der Pol equation, Burgers' equation and the equation of motion are discussed.