Enhancing Open-Vocabulary Object Detection through Multi-Level Fine-Grained Visual-Language Alignment

Traditional object detection systems are typically constrained to predefined categories, limiting their applicability in dynamic environments. In contrast, open-vocabulary object detection (OVD) enables the identification of objects from novel classes not present in the training set. Recent advances in visual-language modeling have led to significant progress of OVD. However, prior works face challenges in either adapting the single-scale image backbone from CLIP to the detection framework or ensuring robust visual-language alignment. We propose Visual-Language Detection (VLDet), a novel framework that revamps feature pyramid for fine-grained visual-language alignment, leading to improved OVD performance. With the VL-PUB module, VLDet effectively exploits the visual-language knowledge from CLIP and adapts the backbone for object detection through feature pyramid. In addition, we introduce the SigRPN block, which incorporates a sigmoid-based anchor-text contrastive alignment loss to improve detection of novel categories. Through extensive experiments, our approach achieves 58.7 AP for novel classes on COCO2017 and 24.8 AP on LVIS, surpassing all state-of-the-art methods and achieving significant improvements of 27.6% and 6.9%, respectively. Furthermore, VLDet also demonstrates superior zero-shot performance on closed-set object detection.

Interaction Models and Generalized Score Matching for Compositional Data

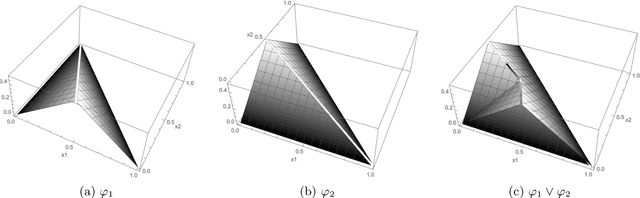
Applications such as the analysis of microbiome data have led to renewed interest in statistical methods for compositional data, i.e., multivariate data in the form of probability vectors that contain relative proportions. In particular, there is considerable interest in modeling interactions among such relative proportions. To this end we propose a class of exponential family models that accommodate general patterns of pairwise interaction while being supported on the probability simplex. Special cases include the family of Dirichlet distributions as well as Aitchison's additive logistic normal distributions. Generally, the distributions we consider have a density that features a difficult to compute normalizing constant. To circumvent this issue, we design effective estimation methods based on generalized versions of score matching. A high-dimensional analysis of our estimation methods shows that the simplex domain is handled as efficiently as previously studied full-dimensional domains.

Generalized Score Matching for General Domains

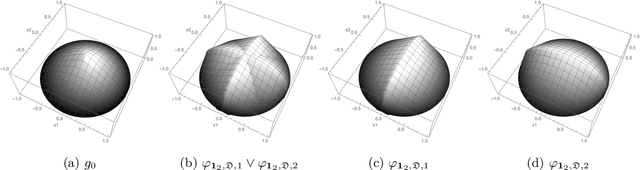
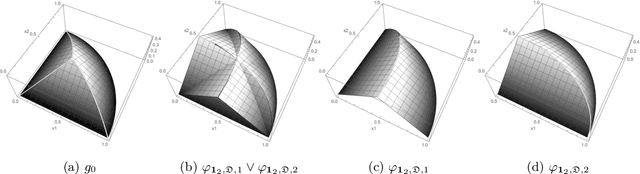
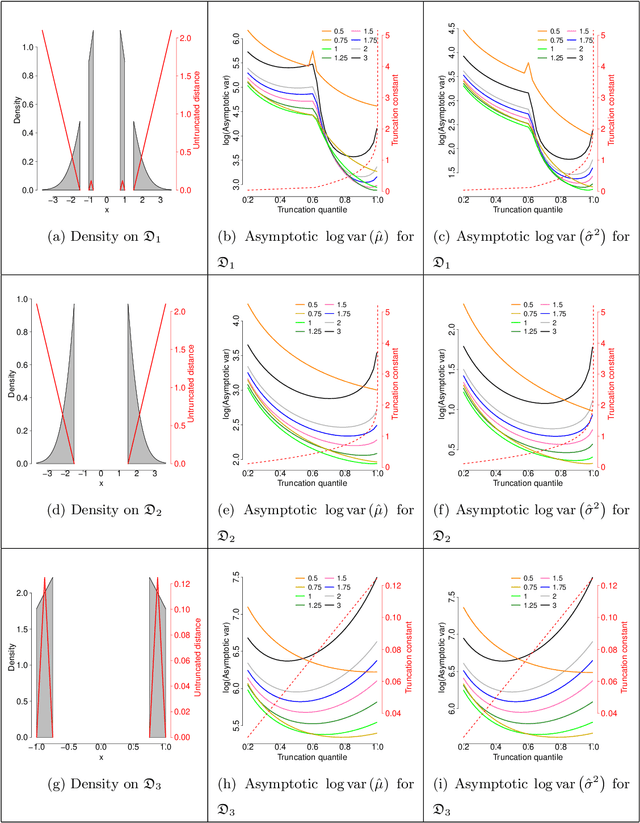
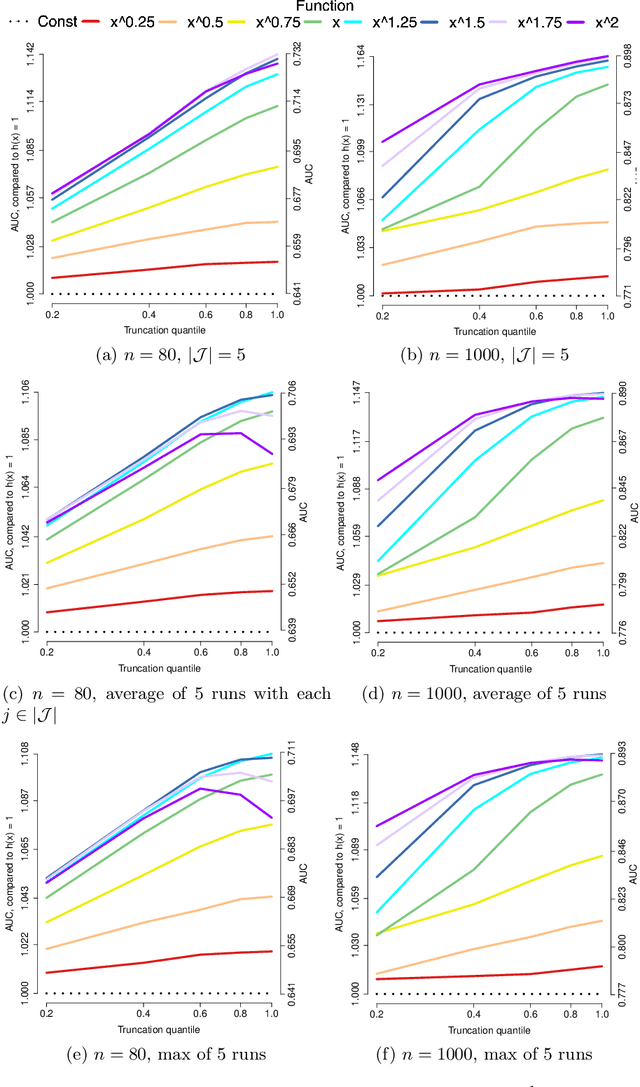
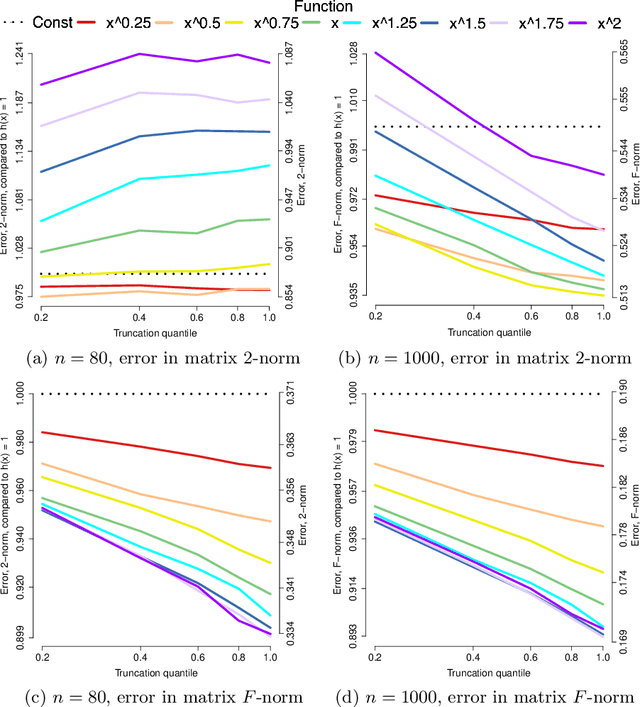
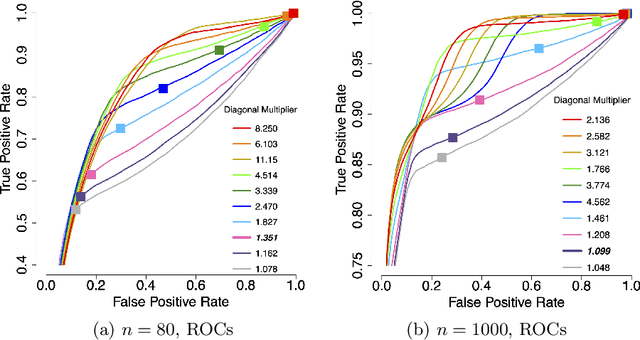
Estimation of density functions supported on general domains arises when the data is naturally restricted to a proper subset of the real space. This problem is complicated by typically intractable normalizing constants. Score matching provides a powerful tool for estimating densities with such intractable normalizing constants, but as originally proposed is limited to densities on $\mathbb{R}^m$ and $\mathbb{R}_+^m$. In this paper, we offer a natural generalization of score matching that accommodates densities supported on a very general class of domains. We apply the framework to truncated graphical and pairwise interaction models, and provide theoretical guarantees for the resulting estimators. We also generalize a recently proposed method from bounded to unbounded domains, and empirically demonstrate the advantages of our method.

Generalized Score Matching for Non-Negative Data

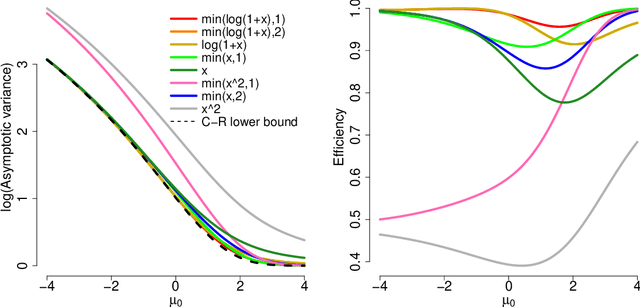
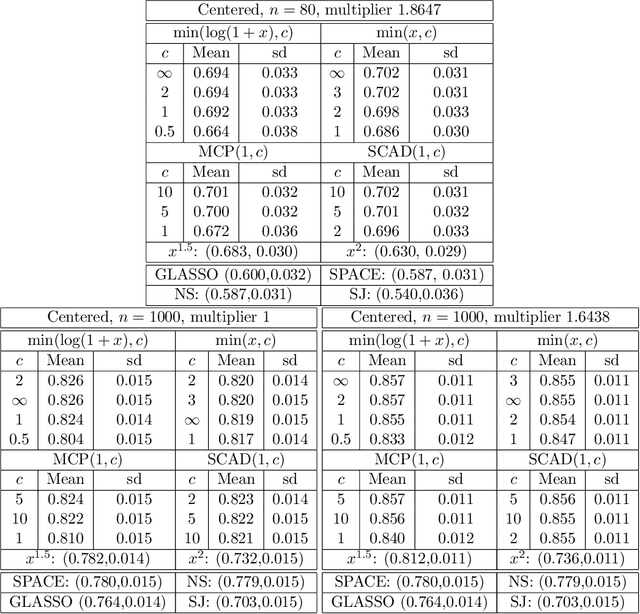
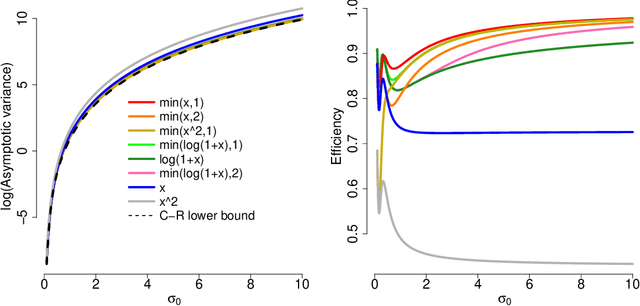
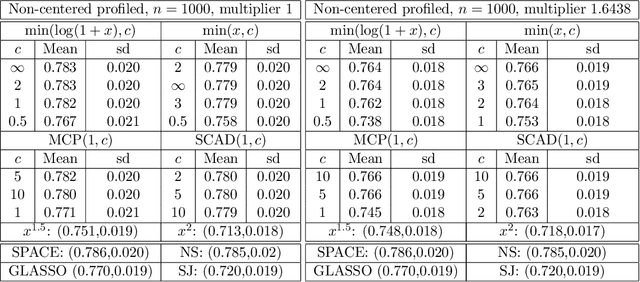
A common challenge in estimating parameters of probability density functions is the intractability of the normalizing constant. While in such cases maximum likelihood estimation may be implemented using numerical integration, the approach becomes computationally intensive. The score matching method of Hyv\"arinen [2005] avoids direct calculation of the normalizing constant and yields closed-form estimates for exponential families of continuous distributions over $\mathbb{R}^m$. Hyv\"arinen [2007] extended the approach to distributions supported on the non-negative orthant, $\mathbb{R}_+^m$. In this paper, we give a generalized form of score matching for non-negative data that improves estimation efficiency. As an example, we consider a general class of pairwise interaction models. Addressing an overlooked inexistence problem, we generalize the regularized score matching method of Lin et al. [2016] and improve its theoretical guarantees for non-negative Gaussian graphical models.