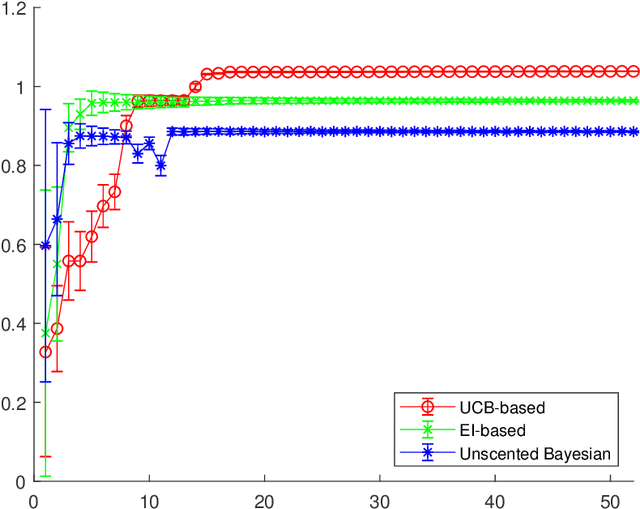
Cost-aware Multi-objective Bayesian optimisation

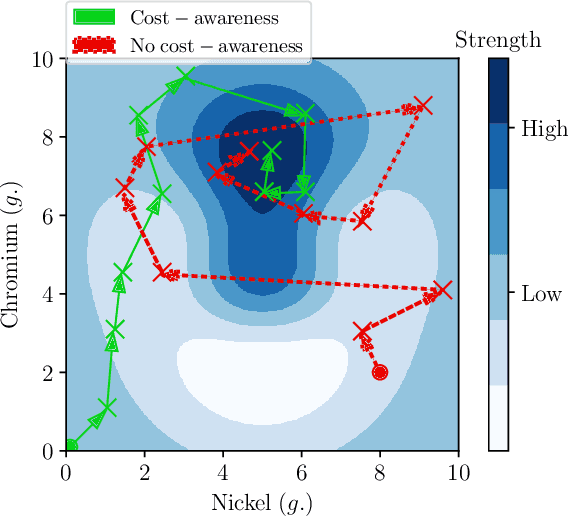
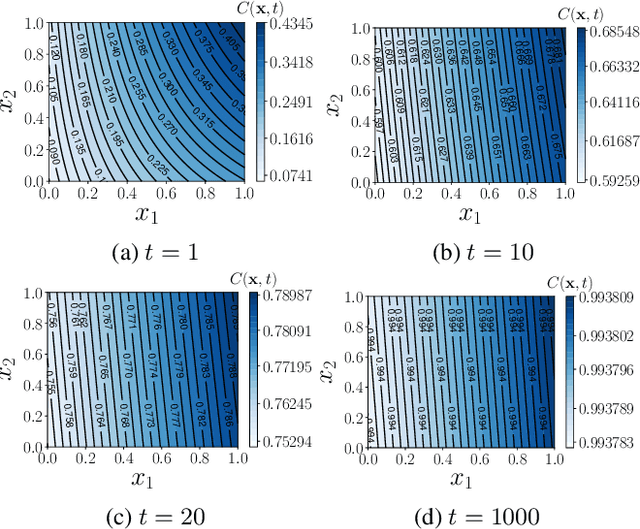
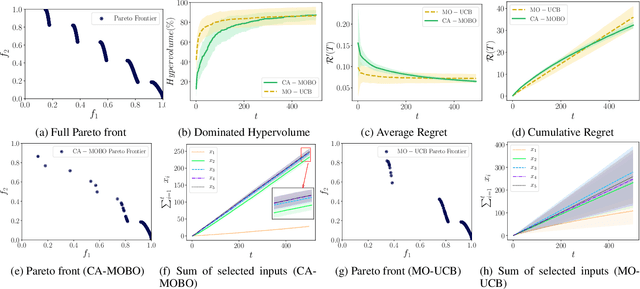
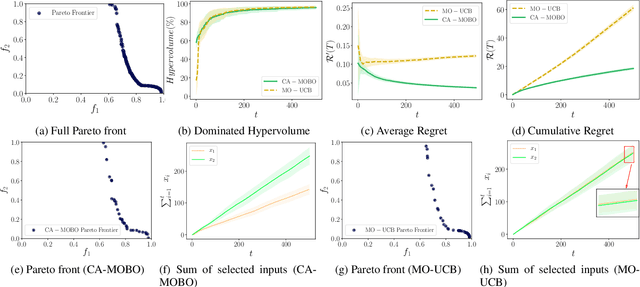
The notion of expense in Bayesian optimisation generally refers to the uniformly expensive cost of function evaluations over the whole search space. However, in some scenarios, the cost of evaluation for black-box objective functions is non-uniform since different inputs from search space may incur different costs for function evaluations. We introduce a cost-aware multi-objective Bayesian optimisation with non-uniform evaluation cost over objective functions by defining cost-aware constraints over the search space. The cost-aware constraints are a sorted tuple of indexes that demonstrate the ordering of dimensions of the search space based on the user's prior knowledge about their cost of usage. We formulate a new multi-objective Bayesian optimisation acquisition function with detailed analysis of the convergence that incorporates this cost-aware constraints while optimising the objective functions. We demonstrate our algorithm based on synthetic and real-world problems in hyperparameter tuning of neural networks and random forests.

Accelerating Experimental Design by Incorporating Experimenter Hunches

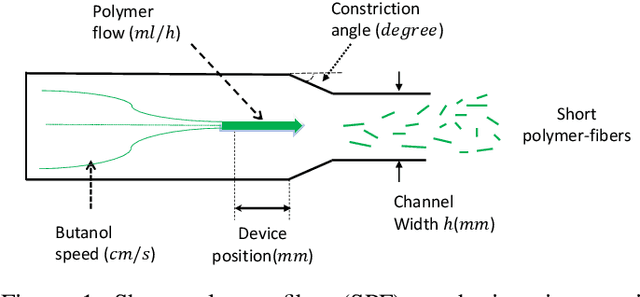
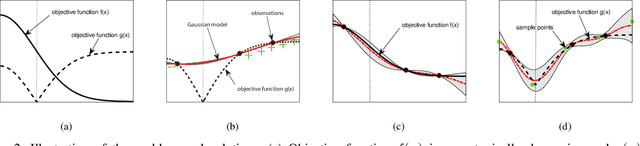
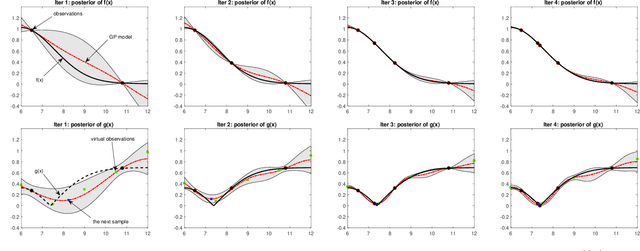
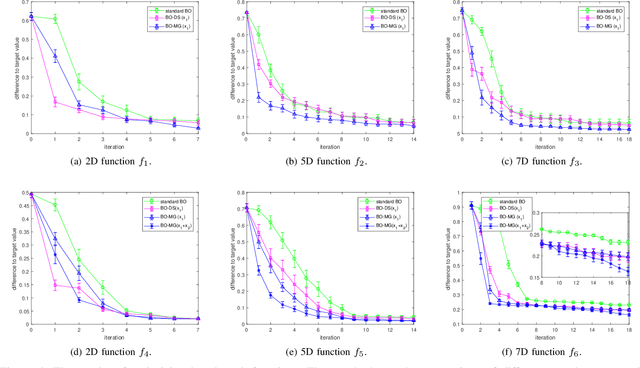
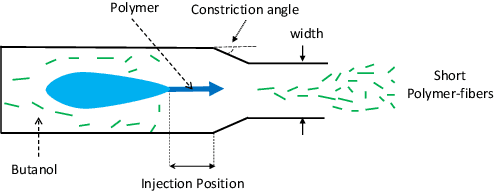
Experimental design is a process of obtaining a product with target property via experimentation. Bayesian optimization offers a sample-efficient tool for experimental design when experiments are expensive. Often, expert experimenters have 'hunches' about the behavior of the experimental system, offering potentials to further improve the efficiency. In this paper, we consider per-variable monotonic trend in the underlying property that results in a unimodal trend in those variables for a target value optimization. For example, sweetness of a candy is monotonic to the sugar content. However, to obtain a target sweetness, the utility of the sugar content becomes a unimodal function, which peaks at the value giving the target sweetness and falls off both ways. In this paper, we propose a novel method to solve such problems that achieves two main objectives: a) the monotonicity information is used to the fullest extent possible, whilst ensuring that b) the convergence guarantee remains intact. This is achieved by a two-stage Gaussian process modeling, where the first stage uses the monotonicity trend to model the underlying property, and the second stage uses `virtual' samples, sampled from the first, to model the target value optimization function. The process is made theoretically consistent by adding appropriate adjustment factor in the posterior computation, necessitated because of using the `virtual' samples. The proposed method is evaluated through both simulations and real world experimental design problems of a) new short polymer fiber with the target length, and b) designing of a new three dimensional porous scaffolding with a target porosity. In all scenarios our method demonstrates faster convergence than the basic Bayesian optimization approach not using such `hunches'.

Sparse Spectrum Gaussian Process for Bayesian Optimisation

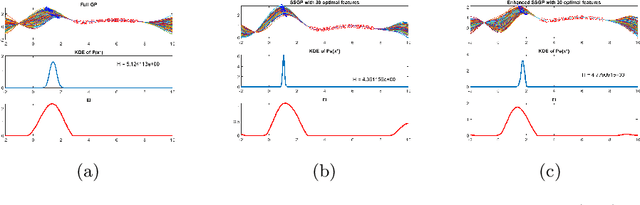
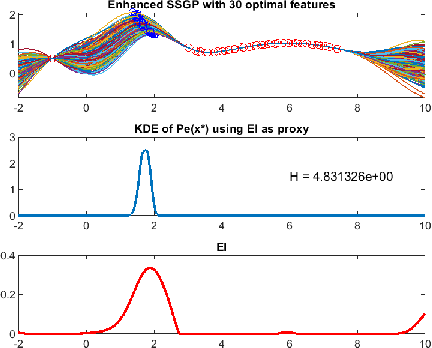
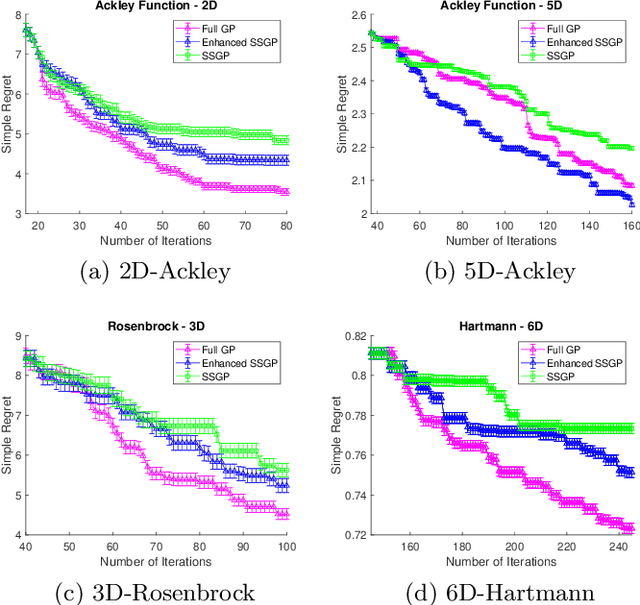
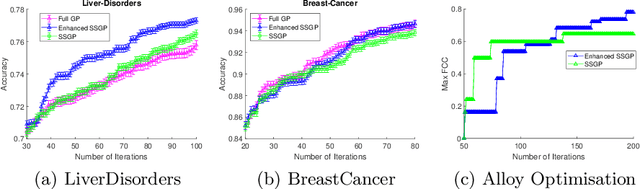
We propose a novel sparse spectrum approximation of Gaussian process (GP) tailored for Bayesian optimisation. Whilst the current sparse spectrum methods provide good approximations for regression problems, it is observed that this particular form of sparse approximations generates an overconfident GP, i.e. it predicts less variance than the original GP. Since the balance between predictive mean and the predictive variance is a key determinant in the success of Bayesian optimisation, the current sparse spectrum methods are less suitable. We derive a regularised marginal likelihood for finding the optimal frequencies in optimisation problems. The regulariser trades the accuracy in the model fitting with the targeted increase in the variance of the resultant GP. We first consider the entropy of the distribution over the maxima as the regulariser that needs to be maximised. Later we show that the Expected Improvement acquisition function can also be used as a proxy for that, thus making the optimisation less computationally expensive. Experiments show an increase in the Bayesian optimisation convergence rate over the vanilla sparse spectrum method.

Stable Bayesian Optimisation via Direct Stability Quantification

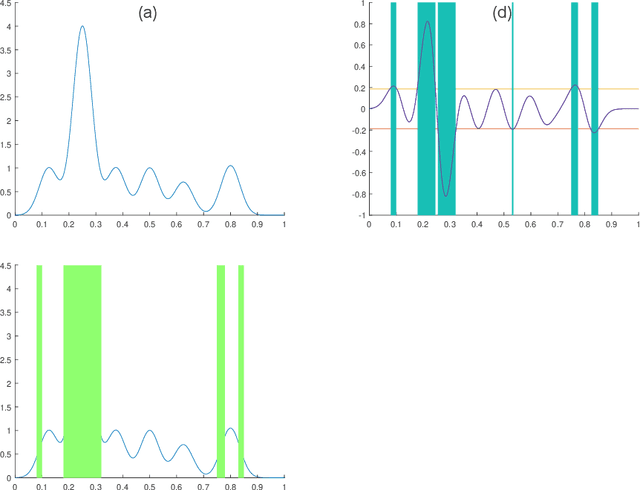
In this paper we consider the problem of finding stable maxima of expensive (to evaluate) functions. We are motivated by the optimisation of physical and industrial processes where, for some input ranges, small and unavoidable variations in inputs lead to unacceptably large variation in outputs. Our approach uses multiple gradient Gaussian Process models to estimate the probability that worst-case output variation for specified input perturbation exceeded the desired maxima, and these probabilities are then used to (a) guide the optimisation process toward solutions satisfying our stability criteria and (b) post-filter results to find the best stable solution. We exhibit our algorithm on synthetic and real-world problems and demonstrate that it is able to effectively find stable maxima.

Multi-objective Bayesian optimisation with preferences over objectives

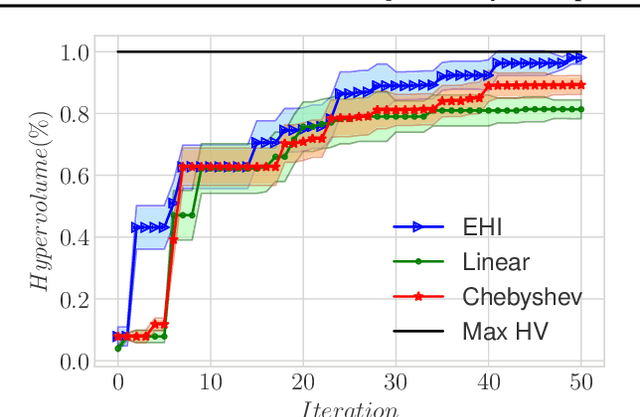
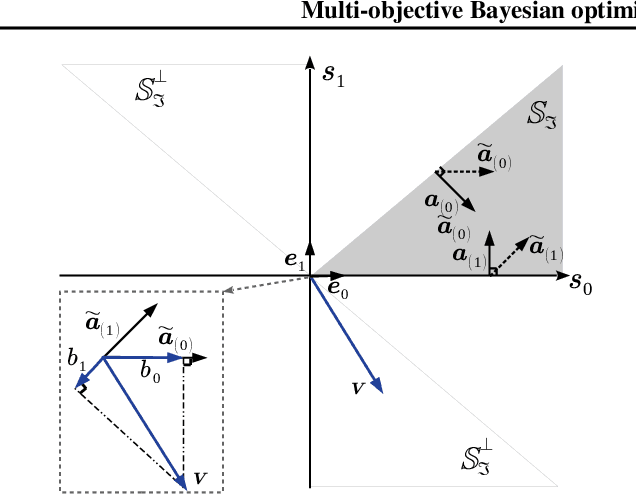
We present a Bayesian multi-objective optimisation algorithm that allows the user to express preference-order constraints on the objectives of the type `objective A is more important than objective B'. Rather than attempting to find a representative subset of the complete Pareto front, our algorithm searches for and returns only those Pareto-optimal points that satisfy these constraints. We formulate a new acquisition function based on expected improvement in dominated hypervolume (EHI) to ensure that the subset of Pareto front satisfying the constraints is thoroughly explored. The hypervolume calculation only includes those points that satisfy the preference-order constraints, where the probability of a point satisfying the constraints is calculated from a gradient Gaussian Process model. We demonstrate our algorithm on both synthetic and real-world problems.

Fast Hyperparameter Tuning using Bayesian Optimization with Directional Derivatives

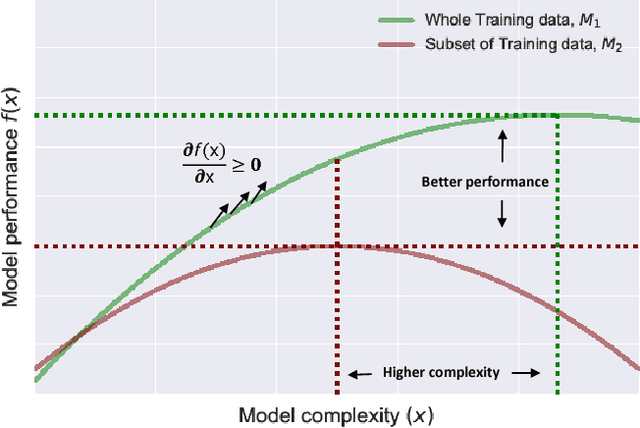
In this paper we develop a Bayesian optimization based hyperparameter tuning framework inspired by statistical learning theory for classifiers. We utilize two key facts from PAC learning theory; the generalization bound will be higher for a small subset of data compared to the whole, and the highest accuracy for a small subset of data can be achieved with a simple model. We initially tune the hyperparameters on a small subset of training data using Bayesian optimization. While tuning the hyperparameters on the whole training data, we leverage the insights from the learning theory to seek more complex models. We realize this by using directional derivative signs strategically placed in the hyperparameter search space to seek a more complex model than the one obtained with small data. We demonstrate the performance of our method on the tasks of tuning the hyperparameters of several machine learning algorithms.

Practical Batch Bayesian Optimization for Less Expensive Functions

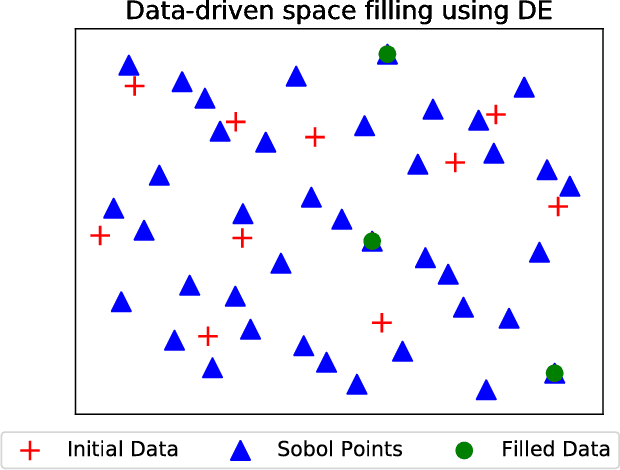
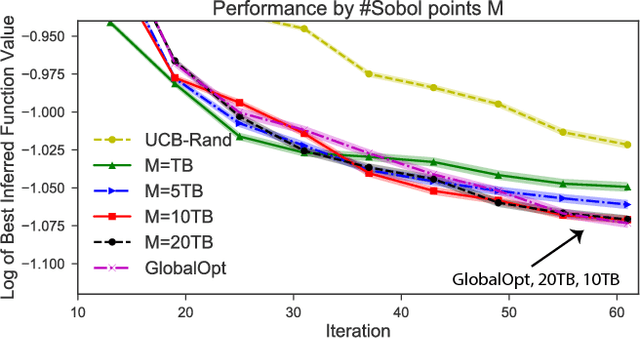
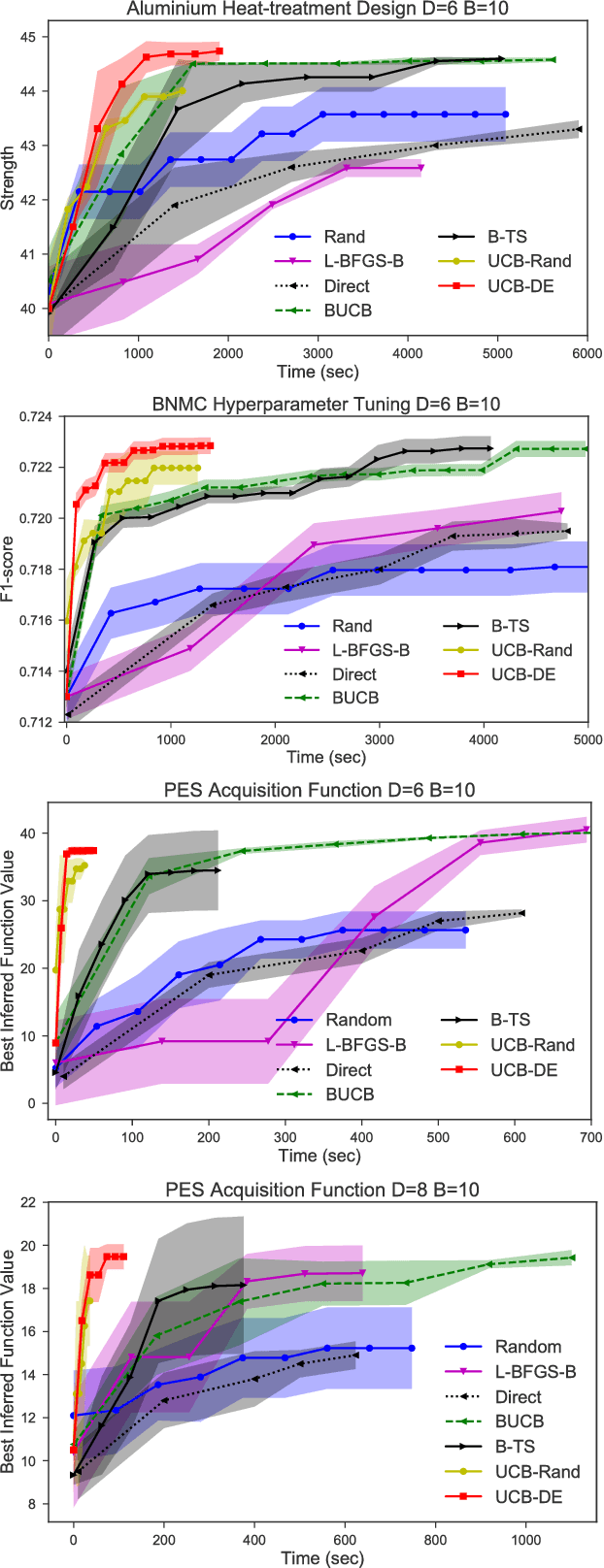
Bayesian optimization (BO) and its batch extensions are successful for optimizing expensive black-box functions. However, these traditional BO approaches are not yet ideal for optimizing less expensive functions when the computational cost of BO can dominate the cost of evaluating the blackbox function. Examples of these less expensive functions are cheap machine learning models, inexpensive physical experiment through simulators, and acquisition function optimization in Bayesian optimization. In this paper, we consider a batch BO setting for situations where function evaluations are less expensive. Our model is based on a new exploration strategy using geometric distance that provides an alternative way for exploration, selecting a point far from the observed locations. Using that intuition, we propose to use Sobol sequence to guide exploration that will get rid of running multiple global optimization steps as used in previous works. Based on the proposed distance exploration, we present an efficient batch BO approach. We demonstrate that our approach outperforms other baselines and global optimization methods when the function evaluations are less expensive.

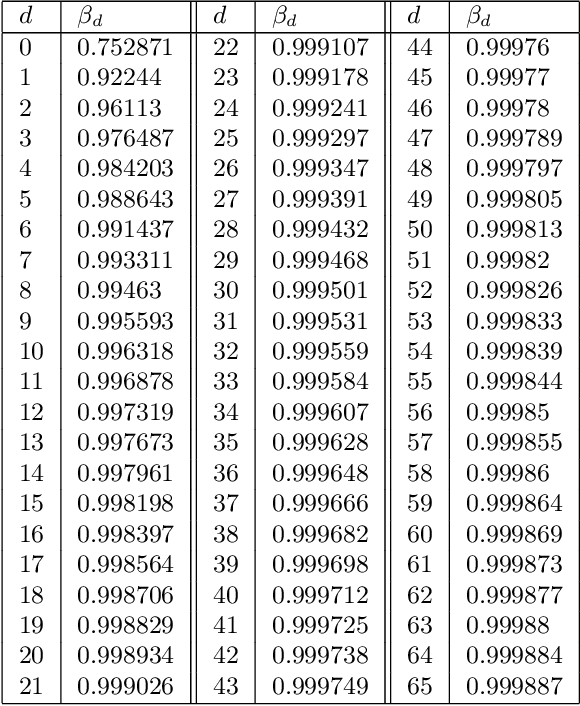
Bayesian functional optimisation with shape prior

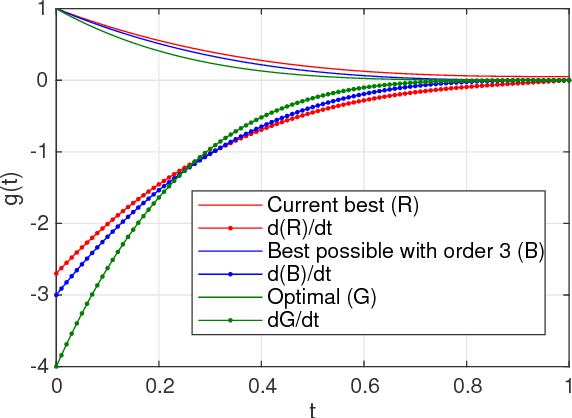
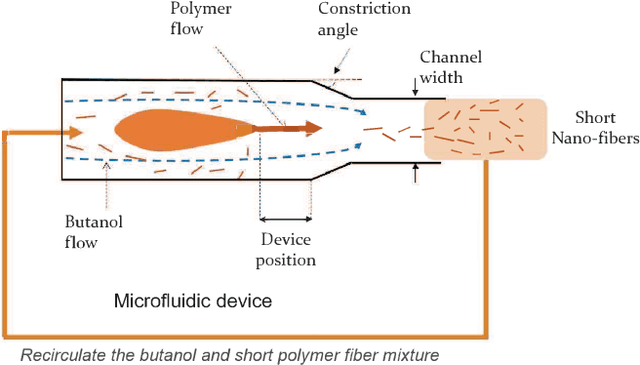
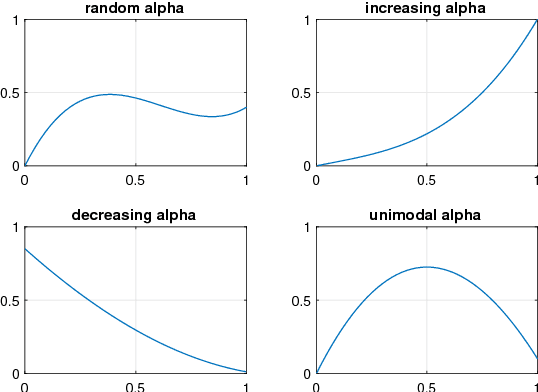
Real world experiments are expensive, and thus it is important to reach a target in minimum number of experiments. Experimental processes often involve control variables that changes over time. Such problems can be formulated as a functional optimisation problem. We develop a novel Bayesian optimisation framework for such functional optimisation of expensive black-box processes. We represent the control function using Bernstein polynomial basis and optimise in the coefficient space. We derive the theory and practice required to dynamically adjust the order of the polynomial degree, and show how prior information about shape can be integrated. We demonstrate the effectiveness of our approach for short polymer fibre design and optimising learning rate schedules for deep networks.

Kernel Pre-Training in Feature Space via m-Kernels

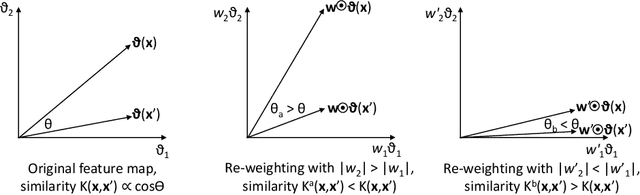
This paper presents a novel approach to kernel tuning. The method presented borrows techniques from reproducing kernel Banach space (RKBS) theory and tensor kernels and leverages them to convert (re-weight in feature space) existing kernel functions into new, problem-specific kernels using auxiliary data. The proposed method is applied to accelerating Bayesian optimisation via covariance (kernel) function pre-tuning for short-polymer fibre manufacture and alloy design.

Covariance Function Pre-Training with m-Kernels for Accelerated Bayesian Optimisation

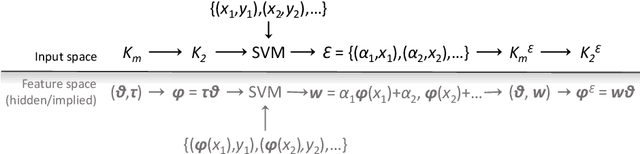
The paper presents a novel approach to direct covariance function learning for Bayesian optimisation, with particular emphasis on experimental design problems where an existing corpus of condensed knowledge is present. The method presented borrows techniques from reproducing kernel Banach space theory (specifically m-kernels) and leverages them to convert (or re-weight) existing covariance functions into new, problem-specific covariance functions. The key advantage of this approach is that rather than relying on the user to manually select (with some hyperparameter tuning and experimentation) an appropriate covariance function it constructs the covariance function to specifically match the problem at hand. The technique is demonstrated on two real-world problems - specifically alloy design and short-polymer fibre manufacturing - as well as a selected test function.