How DREAMS are made: Emulating Satellite Galaxy and Subhalo Populations with Diffusion Models and Point Clouds

The connection between galaxies and their host dark matter (DM) halos is critical to our understanding of cosmology, galaxy formation, and DM physics. To maximize the return of upcoming cosmological surveys, we need an accurate way to model this complex relationship. Many techniques have been developed to model this connection, from Halo Occupation Distribution (HOD) to empirical and semi-analytic models to hydrodynamic. Hydrodynamic simulations can incorporate more detailed astrophysical processes but are computationally expensive; HODs, on the other hand, are computationally cheap but have limited accuracy. In this work, we present NeHOD, a generative framework based on variational diffusion model and Transformer, for painting galaxies/subhalos on top of DM with an accuracy of hydrodynamic simulations but at a computational cost similar to HOD. By modeling galaxies/subhalos as point clouds, instead of binning or voxelization, we can resolve small spatial scales down to the resolution of the simulations. For each halo, NeHOD predicts the positions, velocities, masses, and concentrations of its central and satellite galaxies. We train NeHOD on the TNG-Warm DM suite of the DREAMS project, which consists of 1024 high-resolution zoom-in hydrodynamic simulations of Milky Way-mass halos with varying warm DM mass and astrophysical parameters. We show that our model captures the complex relationships between subhalo properties as a function of the simulation parameters, including the mass functions, stellar-halo mass relations, concentration-mass relations, and spatial clustering. Our method can be used for a large variety of downstream applications, from galaxy clustering to strong lensing studies.

Accuracy-Privacy Trade-off in the Mitigation of Membership Inference Attack in Federated Learning

Over the last few years, federated learning (FL) has emerged as a prominent method in machine learning, emphasizing privacy preservation by allowing multiple clients to collaboratively build a model while keeping their training data private. Despite this focus on privacy, FL models are susceptible to various attacks, including membership inference attacks (MIAs), posing a serious threat to data confidentiality. In a recent study, Rezaei \textit{et al.} revealed the existence of an accuracy-privacy trade-off in deep ensembles and proposed a few fusion strategies to overcome it. In this paper, we aim to explore the relationship between deep ensembles and FL. Specifically, we investigate whether confidence-based metrics derived from deep ensembles apply to FL and whether there is a trade-off between accuracy and privacy in FL with respect to MIA. Empirical investigations illustrate a lack of a non-monotonic correlation between the number of clients and the accuracy-privacy trade-off. By experimenting with different numbers of federated clients, datasets, and confidence-metric-based fusion strategies, we identify and analytically justify the clear existence of the accuracy-privacy trade-off.

MIA-BAD: An Approach for Enhancing Membership Inference Attack and its Mitigation with Federated Learning

The membership inference attack (MIA) is a popular paradigm for compromising the privacy of a machine learning (ML) model. MIA exploits the natural inclination of ML models to overfit upon the training data. MIAs are trained to distinguish between training and testing prediction confidence to infer membership information. Federated Learning (FL) is a privacy-preserving ML paradigm that enables multiple clients to train a unified model without disclosing their private data. In this paper, we propose an enhanced Membership Inference Attack with the Batch-wise generated Attack Dataset (MIA-BAD), a modification to the MIA approach. We investigate that the MIA is more accurate when the attack dataset is generated batch-wise. This quantitatively decreases the attack dataset while qualitatively improving it. We show how training an ML model through FL, has some distinct advantages and investigate how the threat introduced with the proposed MIA-BAD approach can be mitigated with FL approaches. Finally, we demonstrate the qualitative effects of the proposed MIA-BAD methodology by conducting extensive experiments with various target datasets, variable numbers of federated clients, and training batch sizes.

Seven open problems in applied combinatorics

We present and discuss seven different open problems in applied combinatorics. The application areas relevant to this compilation include quantum computing, algorithmic differentiation, topological data analysis, iterative methods, hypergraph cut algorithms, and power systems.

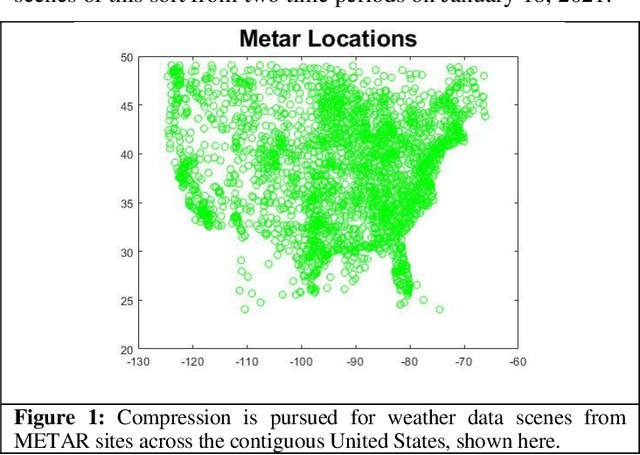
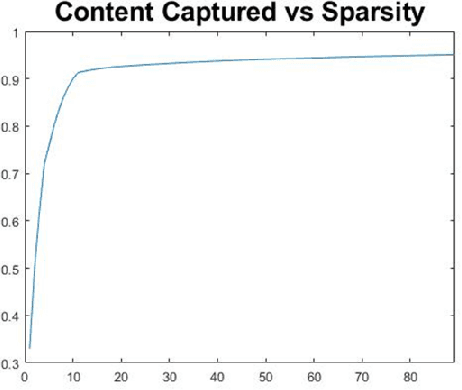
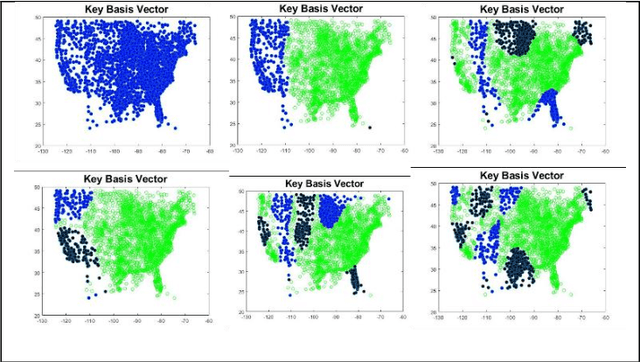
Compressive Representations of Weather Scenes for Strategic Air Traffic Flow Management

Terse representation of high-dimensional weather scene data is explored, in support of strategic air traffic flow management objectives. Specifically, we consider whether aviation-relevant weather scenes are compressible, in the sense that each scene admits a possibly-different sparse representation in a basis of interest. Here, compression of weather scenes extracted from METAR data (including temperature, flight categories, and visibility profiles for the contiguous United States) is examined, for the graph-spectral basis. The scenes are found to be compressible, with 75-95% of the scene content captured using 0.5-4% of the basis vectors. Further, the dominant basis vectors for each scene are seen to identify time-varying spatial characteristics of the weather, and reconstruction from the compressed representation is demonstrated. Finally, potential uses of the compressive representations in strategic TFM design are briefly scoped.

Compressibility of Network Opinion and Spread States in the Laplacian-Eigenvector Basis

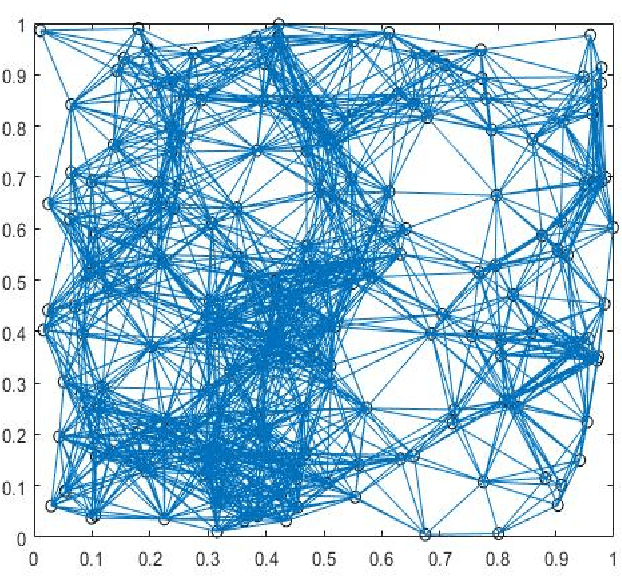
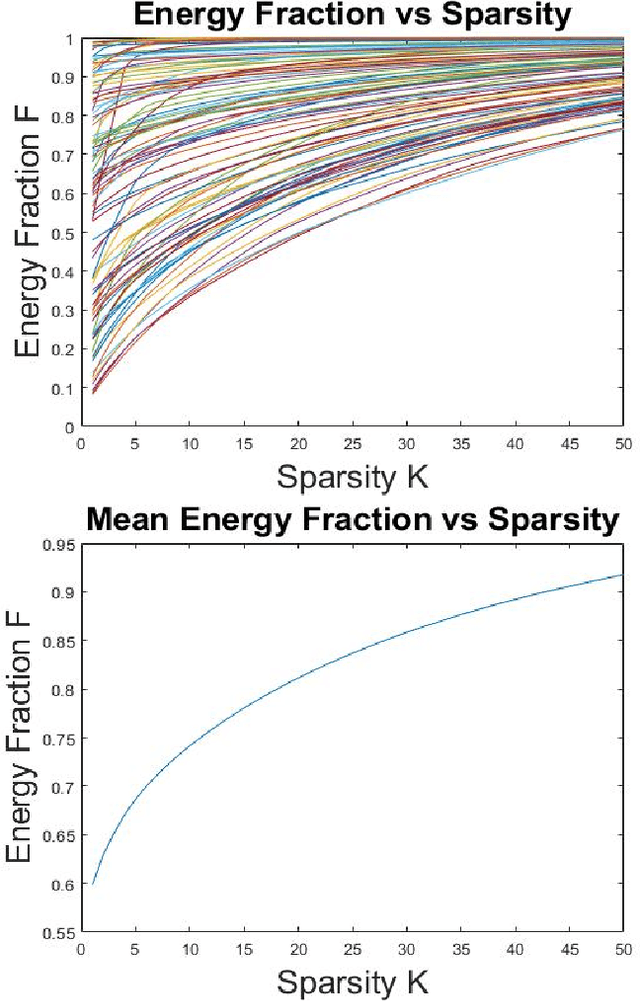
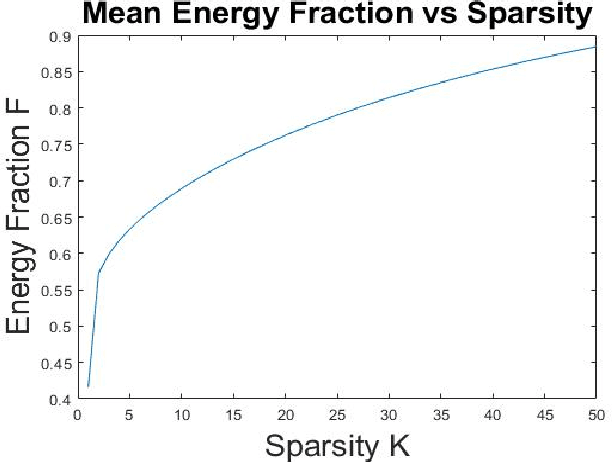
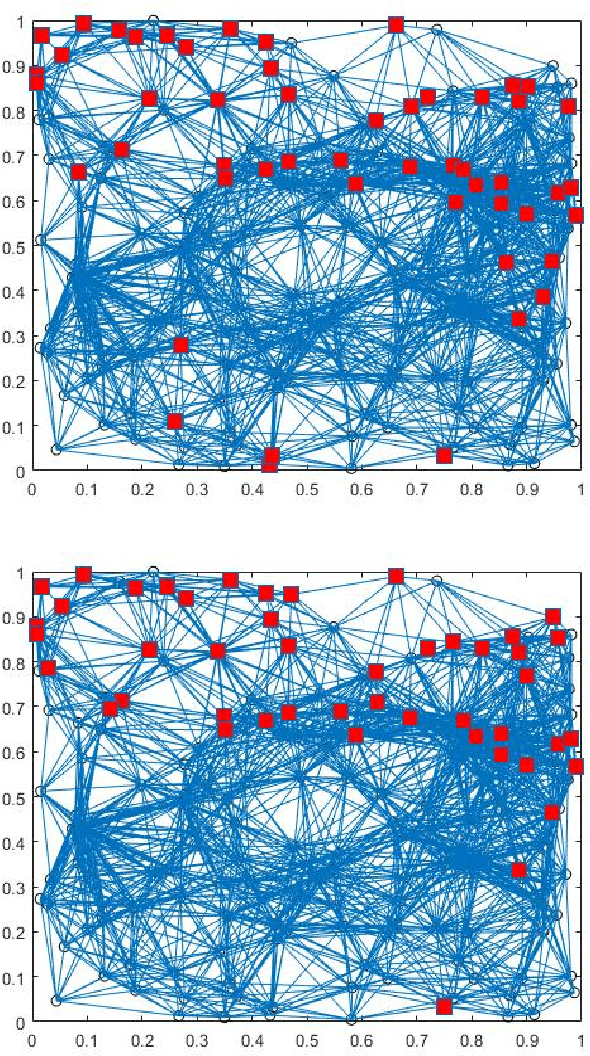
Opinion-evolution and spread processes on networks (e.g., infectious disease spread, opinion formation in social networks) are not only high dimensional but also volatile and multiscale in nature. In this study, we explore whether snapshot data from these processes can admit terse representations. Specifically, using three case studies, we explore whether the data are compressible in the Laplacian-eigenvector basis, in the sense that each snapshot can be approximated well using a (possibly different) small set of basis vectors. The first case study is concerned with a linear consensus model that is subject to a stochastic input at an unknown location; both empirical and formal analyses are used to characterize compressibility. Second, compressibility of state snapshots for a stochastic voter model is assessed via an empirical study. Finally, compressibility is studied for state-level daily COVID-19 positivity-rate data. The three case studies indicate that state snapshots from opinion-evolution and spread processes allow terse representations, which nevertheless capture their rich propagative dynamics.